a+b+c的N次方展开

今天在给儿子看笔记本上的照片的时候，偶然发现了2009年手绘的一张a+b+c的N次方展开图，故写下面的博客以记之，为年轻时代的我点个赞！

20年前的我，一个充满激情的且富有专注力的数学发烧友！

10年前的我，一个无知者无畏的好写代码的疯狂的程序员！

而现在的我，一个被生活荡平了棱角的但是依然坚持理想的程序员。

言归正传，众所周知，a+b的N次方展开满足杨辉三角形。例如：

(a + b) ** 0 = 1                                   |         1
(a + b) ** 1 = a + b                               |       1   1
(a + b) ** 2 = a^2 + 2ab + b^2                     |     1   2   1
(a + b) ** 3 = a^3 + 3a^2b + 3ab^2 + b^3           |   1   3   3   1
(a + b) ** 4 = a^4 + 4a^3b + 6a^2b^2 + 4ab^3 + b^4 | 1   4   6   4   1

国外将杨辉三角形叫做帕斯卡三角形(Pascal's triangle)。 引用维基百科的gif图动态呈现如下：

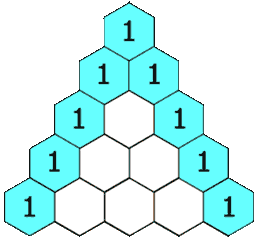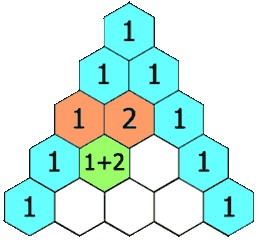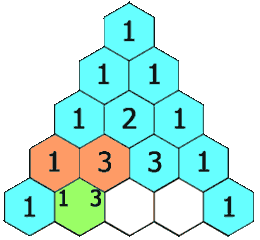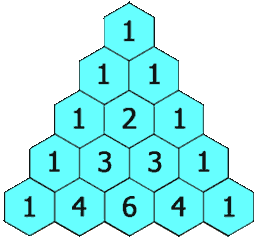
那么， a+b+c的N次方展开是什么样子滴？ 高二（1997年的夏天）的时候（在学完二项式定理后），作为数学发烧友的我，硬是花了一个周末，废寝忘食地纯手工计算了N=0,1,2,3,4,5,6的情况，发现了如下图所示的规律。

注：上图为2009年我用Python实现了(a+b+c)**N后重绘的图片，那时候我已经是一个疯狂的程序员：-）

o abcN.py

 #!/usr/bin/python
 """
 A rough but simple solution to count expression
 (a + b + c) ** n = ?

 By Huanian<li.huanian@gmail.com>
 On May, 2009
 """

 import sys

 def str2exp(s):
         """
         1@a:2-b:1-c:1 => a^2bc
         2@a:3-b:0-c:1 => 2a^3c
         """
         i0, s0 = s.split('@')
         sa, sb, sc = s0.split('-')
         ca, ia = sa.split(':')
         cb, ib = sb.split(':')
         cc, ic = sc.split(':')

         sout = ""
         if i0 != '':
                 sout += i0
         if ia != '':
                 if ia != '':
                         s_ia = "%s^%s" % (ca, ia)
                 else:
                         s_ia = ca
                 sout += s_ia
         if ib != '':
                 if ib != '':
                         s_ib = "%s^%s" % (cb, ib)
                 else:
                         s_ib = cb
                 sout += s_ib
         if ic != '':
                 if ic != '':
                         s_ic = "%s^%s" % (cc, ic)
                 else:
                         s_ic = cc
                 sout += s_ic
         return (sout)

 def list2exp(lin):
         lout = []
         for i in lin:
                 s = str2exp(i)
                 lout.append(s)
         return (' + '.join(lout))

 def merge_list(lin):
         """
         merge index of same entries
         e.g.  [1@a:1-b:2-c:0, 2@a:2-b:1:-c:0, 1@a:1-b:2-c:0]
         ====> [2@a:1-b:2-c:0, 2@a:2-b:1:-c:0]
         """
         ltmp = []
         for i in lin:
                 n, s = i.split('@')
                 if s not in ltmp:
                         ltmp.append(s)

         lout = []
         for i in ltmp:
                 m = 0
                 for j in lin:
                         n, s = j.split('@')
                         if i == s:
                                 m += int(n)
                 s = "%d@%s" % (m, i)
                 lout.append(s)
         return (lout)

 def exp_xx_1(lin):
         """ list * ( a + b + c) """
         lout = []
         for i in lin:
                 n0, s0 = i.split('@')
                 sa, sb, sc = s0.split('-')
                 ca, ia = sa.split(':')
                 cb, ib = sb.split(':')
                 cc, ic = sc.split(':')
                 iia = int(ia)
                 iib = int(ib)
                 iic = int(ic)
                 for c in ['a', 'b', 'c']:
                         iia1 = iia
                         iib1 = iib
                         iic1 = iic
                         if c == ca:
                                 iia1 += 1
                         elif c == cb:
                                 iib1 += 1
                         elif c == cc:
                                 iic1 += 1
                         else:
                                 pass
                         s = "%s@a:%d-b:%d-c:%d" % (n0, iia1, iib1, iic1)
                         lout.append(s)
         return (merge_list(lout))

 def exp_xx_n(lin, n):
         if n == 0:
                 return ('')
         ltmp = lin
         lout = ltmp
         i = 1
         while i < n:
                 lout = exp_xx_1(ltmp)
                 ltmp = lout
                 i += 1
         s = list2exp(lout)
         return (s)

 def print2(s):
         sys.stderr.write("%s\n" % s)

 def main(argc, argv):
         if argc != 2:
                 print2("Usage: %s <num>" % argv[0])
                 print2("e.g.   %s 1"     % argv[0])
                 print2("       (a + b + c) ** 1 = a + b + c")
                 return 1

         imax = 64 # cost about 180s
         n = int(argv[1])
         if n > imax:
                 print2("Your num=%d is too big, <= %d is better" % (n, imax))
                 return 1

         # string = "a + b + c" ==> list
         l = ['1@a:1-b:0-c:0', '1@a:0-b:1-c:0', '1@a:0-b:0-c:1']
         # times it now...
         s = exp_xx_n(l, n)
         print "(a + b + c) ** %d = %s" % (n, s)

         return (0)

 if __name__ == '__main__':
         argv = sys.argv
         argc = len(argv)
         sys.exit(main(argc, argv))

o 运行N=0..8

$ ./abcN.py 0
(a + b + c) ** 0 = 1

$ ./abcN.py 1
(a + b + c) ** 1 = a + b + c

$ ./abcN.py 2
(a + b + c) ** 2 = a^2 + 2ab + 2ac + b^2 + 2bc + c^2

$ ./abcN.py 3
(a + b + c) ** 3 = a^3 + 3a^2b + 3a^2c + 3ab^2 + 6abc + 3ac^2 + b^3 + 3b^2c + 3bc^2 + c^3

$ ./abcN.py 4
(a + b + c) ** 4 = a^4 + 4a^3b + 4a^3c + 6a^2b^2 + 12a^2bc + 6a^2c^2 + 4ab^3 + 12ab^2c + 12abc^2 + 4ac^3 + b^4 + 4b^3c + 6b^2c^2 + 4bc^3 + c^4

$ ./abcN.py 5
(a + b + c) ** 5 = a^5 + 5a^4b + 5a^4c + 10a^3b^2 + 20a^3bc + 10a^3c^2 + 10a^2b^3 + 30a^2b^2c + 30a^2bc^2 + 10a^2c^3 + 5ab^4 + 20ab^3c + 30ab^2c^2 + 20abc^3 + 5ac^4 + b^5 + 5b^4c + 10b^3c^2 + 10b^2c^3 + 5bc^4 + c^5

$ ./abcN.py 6
(a + b + c) ** 6 = a^6 + 6a^5b + 6a^5c + 15a^4b^2 + 30a^4bc + 15a^4c^2 + 20a^3b^3 + 60a^3b^2c + 60a^3bc^2 + 20a^3c^3 + 15a^2b^4 + 60a^2b^3c + 90a^2b^2c^2 + 60a^2bc^3 + 15a^2c^4 + 6ab^5 + 30ab^4c + 60ab^3c^2 + 60ab^2c^3 + 30abc^4 + 6ac^5 + b^6 + 6b^5c + 15b^4c^2 + 20b^3c^3 + 15b^2c^4 + 6bc^5 + c^6

$ ./abcN.py 7
(a + b + c) ** 7 = a^7 + 7a^6b + 7a^6c + 21a^5b^2 + 42a^5bc + 21a^5c^2 + 35a^4b^3 + 105a^4b^2c + 105a^4bc^2 + 35a^4c^3 + 35a^3b^4 + 140a^3b^3c + 210a^3b^2c^2 + 140a^3bc^3 + 35a^3c^4 + 21a^2b^5 + 105a^2b^4c + 210a^2b^3c^2 + 210a^2b^2c^3 + 105a^2bc^4 + 21a^2c^5 + 7ab^6 + 42ab^5c + 105ab^4c^2 + 140ab^3c^3 + 105ab^2c^4 + 42abc^5 + 7ac^6 + b^7 + 7b^6c + 21b^5c^2 + 35b^4c^3 + 35b^3c^4 + 21b^2c^5 + 7bc^6 + c^7

$ ./abcN.py 8
(a + b + c) ** 8 = a^8 + 8a^7b + 8a^7c + 28a^6b^2 + 56a^6bc + 28a^6c^2 + 56a^5b^3 + 168a^5b^2c + 168a^5bc^2 + 56a^5c^3 + 70a^4b^4 + 280a^4b^3c + 420a^4b^2c^2 + 280a^4bc^3 + 70a^4c^4 + 56a^3b^5 + 280a^3b^4c + 560a^3b^3c^2 + 560a^3b^2c^3 + 280a^3bc^4 + 56a^3c^5 + 28a^2b^6 + 168a^2b^5c + 420a^2b^4c^2 + 560a^2b^3c^3 + 420a^2b^2c^4 + 168a^2bc^5 + 28a^2c^6 + 8ab^7 + 56ab^6c + 168ab^5c^2 + 280ab^4c^3 + 280ab^3c^4 + 168ab^2c^5 + 56abc^6 + 8ac^7 + b^8 + 8b^7c + 28b^6c^2 + 56b^5c^3 + 70b^4c^4 + 56b^3c^5 + 28b^2c^6 + 8bc^7 + c^8