matlab中的决策树
1.函数
view(t)%画出决策树
prune %剪枝决策树
t2=prune(t,'level','level'/'node')
%level:0 不剪枝 1 剪掉最后一层 2 最后两层
%node: 剪掉第node个分支后的所有
eval %预测
yfit=eval(t,x)
[yfit,nodes,cnum]=eval(t,x)
% x预测样本 yfit 预测结果 nodes 返回样本所处节点位置
% cnum 返回约车类别
2.示例
load fisheriris
t=classregtree(meas,species,'Name',{'sl','sw','pl','pw'});
view(t)
t2=prune(t,'level',1);
t2.view
[yfit,nodes,cnums]=eval(t,meas);
结果:
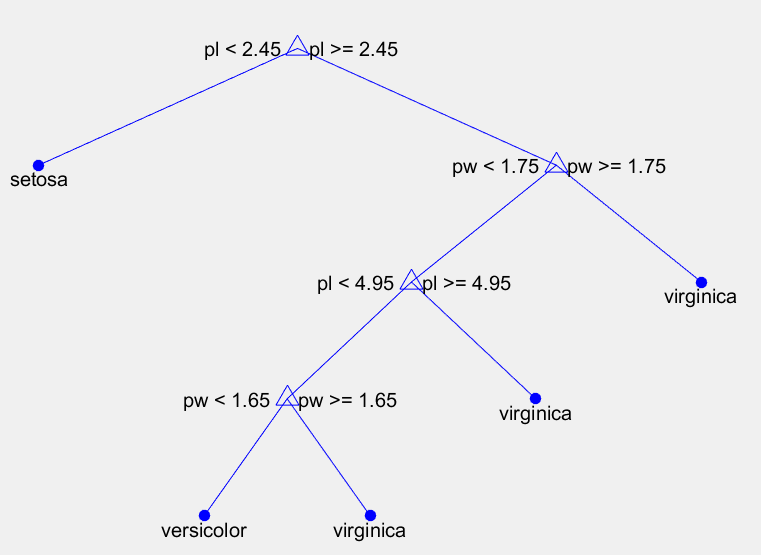
t2:
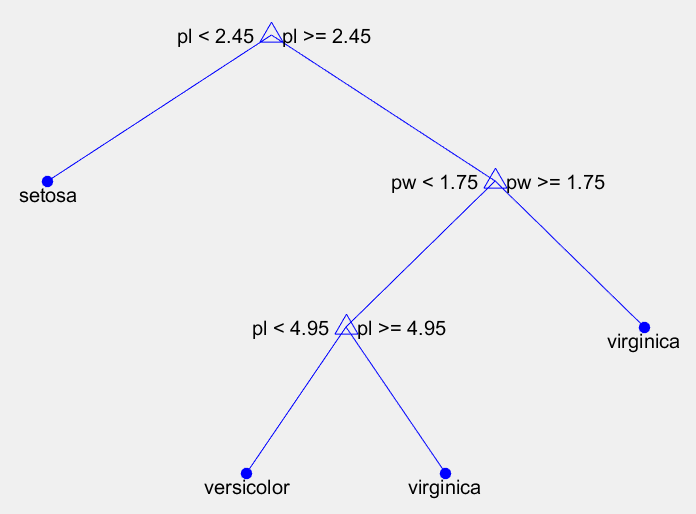
3.fitctree
load fisheriris
t = fitctree(meas,species,'PredictorNames',{'SL' 'SW' 'PL' 'PW'});
view(t,'Mode','graph')
结果:
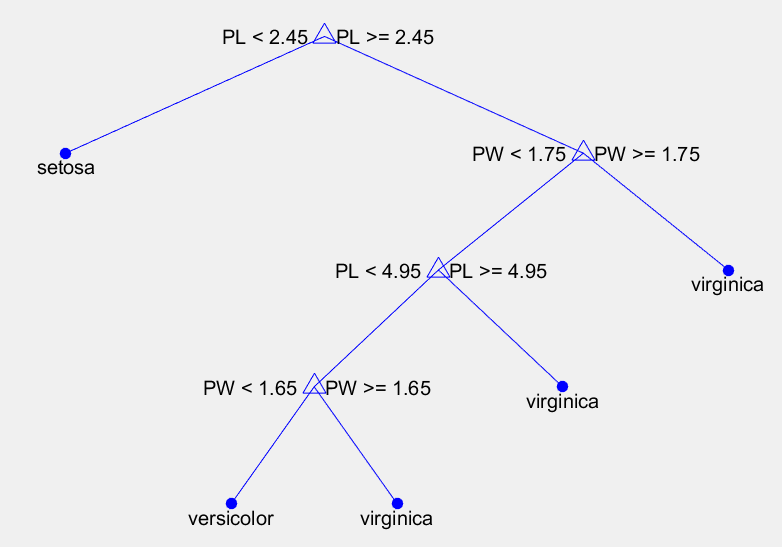
matlab中的决策树的更多相关文章
- MATLAB中绘制质点轨迹动图并保存成GIF
工作需要在MATLAB中绘制质点轨迹并保存成GIF以便展示. 绘制质点轨迹动图可用comet和comet3命令,使用例子如下: t = 0:.01:2*pi;x = cos(2*t).*(cos(t) ...
- matlab 中 eps 的分析
eps(a)是|a|与大于|a|的最小的浮点数之间的距离,距离越小表示精度越高.默认a=1: 这里直接在matlab中输入:eps == eps(1)(true). 我们知道浮点数其实是离散的,有限的 ...
- matlab中patch函数的用法
http://blog.sina.com.cn/s/blog_707b64550100z1nz.html matlab中patch函数的用法——emily (2011-11-18 17:20:33) ...
- paper 121 :matlab中imresize函数
转自:http://www.cnblogs.com/rong86/p/3558344.html matlab中函数imresize简介: 函数功能:该函数用于对图像做缩放处理. 调用格式: B = i ...
- MATLAB中FFT的使用方法
MATLAB中FFT的使用方法 说明:以下资源来源于<数字信号处理的MATLAB实现>万永革主编 一.调用方法X=FFT(x):X=FFT(x,N):x=IFFT(X);x=IFFT(X, ...
- MATLAB中fft函数的正确使用方法
问题来源:在阅读莱昂斯的<数字信号处理>第三章离散傅里叶变换时,试图验证实数偶对称信号的傅里叶变换实部为偶对称的且虚部为零.验证失败.验证信号为矩形信号,结果显示虚部是不为零且最大幅值等于 ...
- Matlab中的一些小技巧
(转于它处,仅供参考) 1.. Ctrl+C 中断正在执行的操作 如果程序不小心进入死循环,或者计算时间太长,可以在命令窗口中使用Ctrl+c来中断.MATLAB这时可能正疲于应付,响应会有些滞后. ...
- Matlab中给figure添加图例(legend),标题(title)和颜色(color)
在Matlab绘图过程中,尤其是需要将多个图绘制在相同的坐标轴中时,通常需要将不同的曲线设置成为不同的颜色.此外,为了直观,还需要给这张图标增添标题和图例.这篇文章展示了在Matlab的绘图窗口(fi ...
- MATLAB中取整函数(fix, floor, ceil, round)的使用
MATLAB取整函数 1)fix(x) : 截尾取整. >> fix( [3.12 -3.12]) ans = 3 -3(2)floor(x):不超过x 的最大整数.(高斯取整) & ...
随机推荐
- WPF中使用相对资源来进行绑定,数据源是通过DataContext来指定的
1. 最外层是Window是对象,Window的ItemsControl使用了ItemsTemplate,然后在ItemsTemplate中要绑定Language属性, 而整个Window的数据源是通 ...
- cnblog博客停用
本博客从今日起停止更新,后续的文章将会发布在新的博客mrbackkom.github.io
- [javaSE] 集合工具类(Collections-sort)
java为我们提供了一个集合的工具类,方便我们对集合进行操作,里面的方法都是静态方法. Collections.sort()方法,参数:List<T>集合对象,这个对象带着泛型,是为了保证 ...
- 十二、spark MLlib的scala示例
简介 spark MLlib官网:http://spark.apache.org/docs/latest/ml-guide.html mllib是spark core之上的算法库,包含了丰富的机器学习 ...
- 关于java异常try catch finally的一道题
这两天,有人咨询我一道关于java基础的题,具体代码如下: private static int m1() { int a = 10; try { a = 20; throw new RuntimeE ...
- idea新建maven多模块spring boot项目
1.新建一个maven多模块项目,比如这种结构: maven-demo |--demo-common |--demo-order |--demo-user 2.先新建一个maven项目,在maven项 ...
- 《JavaWeb从入门到改行》JSP+EL+JSTL大杂烩汤
title: Servlet之JSP tags: [] notebook: javaWEB --- JSP是什么 ? JSP就是Servlet,全名是"JavaServer Pages&qu ...
- springcloud 实战 feign使用中遇到的相关问题
springcloud 实战 feign使用中遇到的相关问题 1.使用feign客户端调用其他微服务时,session没有传递成功,sessionId不一样. /** * @author xbchen ...
- Web服务器学习总结(一):web服务器简介
一.WEB服务器 1.1.WEB服务器简介 1.Web服务器是指驻留于因特网上某种类型计算机的程序,是可以向发出请求的浏览器提供文档的程序.当Web浏览器(客户端)连到服务器上并请求文件时,服务器将处 ...
- mac上调整phpstorm和webstorm的使用内存(默认是128m-750m) 避免卡顿
For Mac Only WebStorm/phpstrom用起来一卡一卡,如今才发现是它的默认内存配置太弱.修改之: 修改phpstrom vi /Applications/PhpStorm.app ...
