【Learning】一步步地解释Link-cut Tree

简介

　　Link-cut Tree，简称LCT。

　　干什么的？它是树链剖分的升级版，可以看做是动态的树剖。

　　树剖专攻静态树问题；LCT专攻动态树问题，因为此时的树剖面对动态树问题已经无能为力了（动态树问题通常夹杂着树的操作，如删边与连边。这是线段树无法应对的）。

　　LCT难写吗？不难写啊...

预备知识：Splay（没有接触也没有关系，打一打LCT也差不多懂了）、树链剖分。

---

1. LCT概念

　　树链剖分把树分成若干条重链，对于每条重链，用线段树来维护信息。利用各线段树的信息来得到答案。

　　模仿一下：

• • LCT把树分成若干条重链：

　　　　　  这是假的重链！树剖是挑选重儿子来延续重链；而LCT的重链是随缘的......

　　　　　  我们先不管这里的重链是怎么确定的，因为在LCT中，重链是可以随时更改的！

• • $access(u)$，这是我们的更改操作。作用是将$u$到原树根节点的一路都变成重链，同时，经过节点将会与原本属于的重链断开，如图，这是我们要维护的原树：

　　　　　　

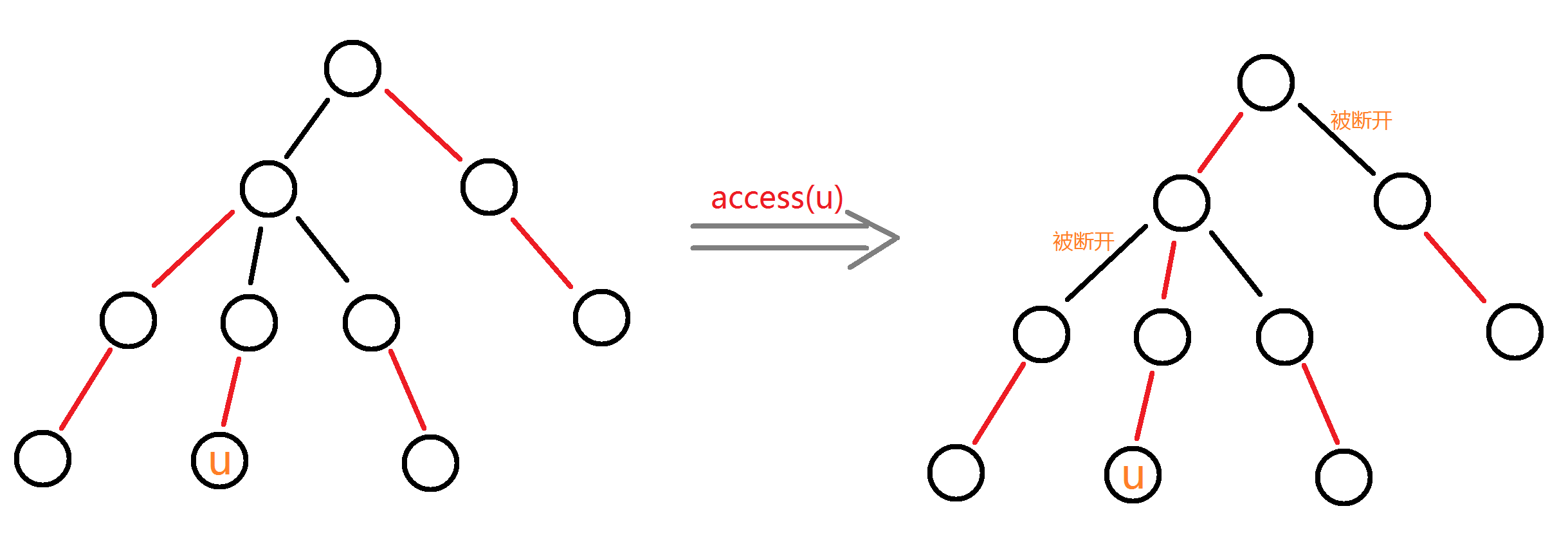
• • 对于每条重链，我们用一棵Splay来维护信息，利用各Splay的信息来得到答案。

---

2. 存储方式

　　LCT是怎么存储的？其中涉及到的$access$操作可能会对Splay进行删点或加点......

　　我们的每条重链的Splay，都是连在一起的，但又是相互独立的！看图：

　　

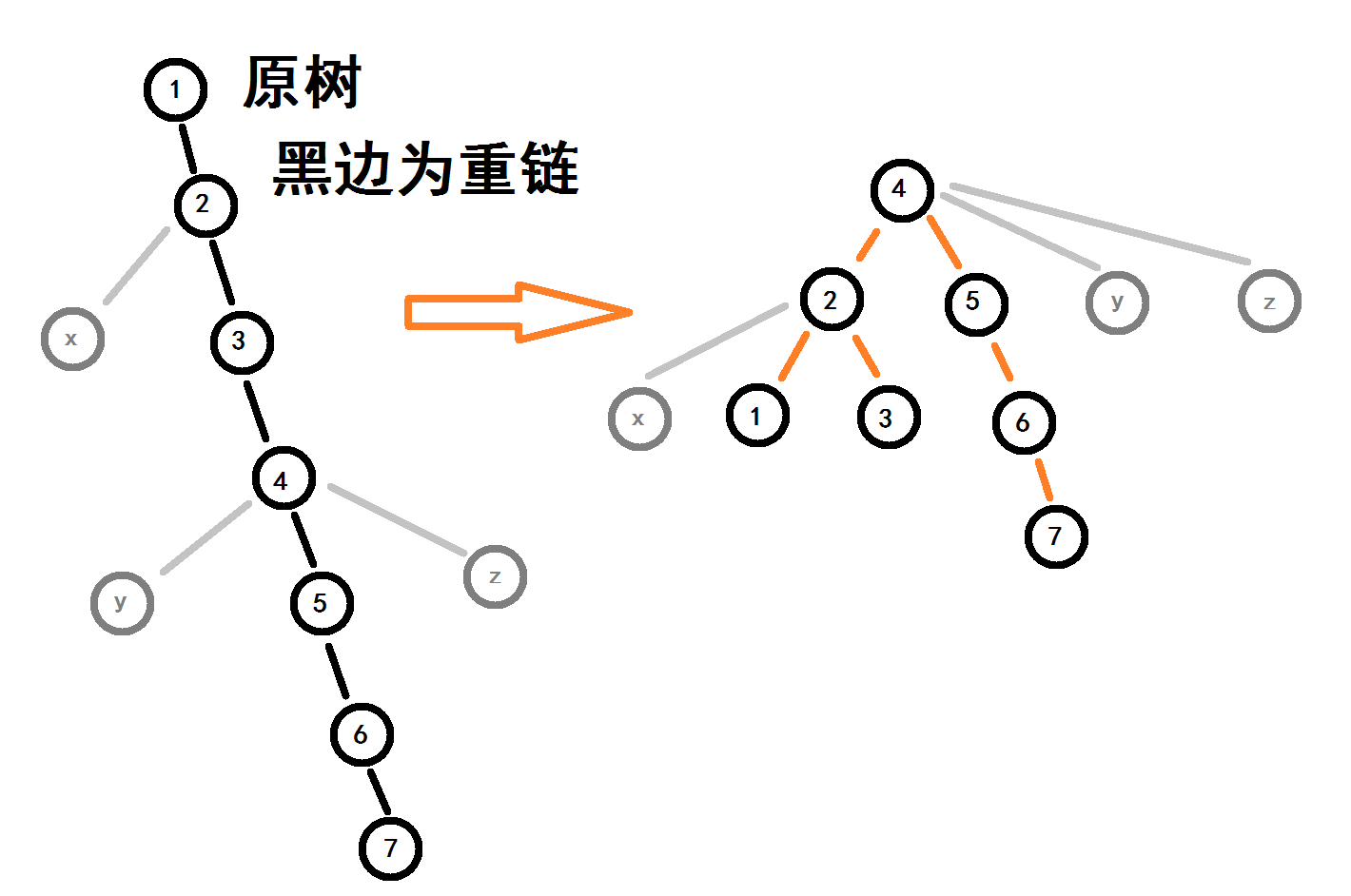
　　橙色边为每棵Splay，灰色边表示的是Splay之间的连接边。

　　每棵Splay储存照常，Splay的中序遍历即重链节点从浅到深的排列。每棵Splay内节点的关系可能和原树不同，但是与其他Splay连边的节点没有改变。

　　由此，每棵Splay可以维护一条链上的信息。

　　但只有每棵Splay的根节点能连向其他Splay的某个节点（灰色边）。Splay根节点$root$记录它的父亲是谁（有的Splay根节点$root$没有父亲），而它的父亲并不记录自己有这个儿子$root$。

　　发现，每一个节点，都能够通过一直走父亲（不管是亲生还是认领的），走到某一个点，这个点就是上节提到的原树根节点，不同于Splay的根节点。

　　

---

3. 基础函数（以下基本都是经典函数）

　　我们需要一个函数来判断当前节点$u$是否为所属Splay的根节点：

　　　　

bool isroot(int u){
    return ch[fa[u]][]!=u&&ch[fa[u]][]!=u;
}

　　即父亲的左右儿子都不是自己，说明此节点是Splay的根节点，它的父亲并不记录自己。

　　需要一个函数判断当前节点$u$是父亲节点的左儿子还是右儿子：

　　

int who(int u){
    return ch[fa[u]][]==u;
} 

　　如果是左儿子，返回0；否则返回1。

　　更新Splay信息函数，作用是收集左右儿子的信息。这里以最大值举例：

void update(int u){
    if(!u) return;
    info[u]=max(w[u],max(info[ch[u][]],info[ch[u][]]));
}

　　

　　经典的Splay翻转打标记函数reverse、单次下传函数pushdownOnce、一路下传函数pushdown、旋转函数rotate和伸展函数splay，没有什么特殊的地方：

　　

void reverse(int u){
    rev[u]^=;
    swap(ch[u][],ch[u][]);
}
//为u打上翻转标记

void pushdownOnce(int u){
    if(rev[u]){
        if(ch[u][]) reverse(ch[u][]);
        if(ch[u][]) reverse(ch[u][]);
        rev[u]=;
    }
}
//单次下传

void pushdown(int u){
    if(!isroot(u)) pushdown(fa[u]);
    pushdownOnce(u);
}
//从当前Splay的根节点一路下传到u，把一路的翻转都处理掉

void rotate(int u){
    int f=fa[u],g=fa[f],c=who(u);
    if(!isroot(f))
        ch[g][who(f)]=u;
    fa[u]=g;
    ch[f][c]=ch[u][c^]; fa[ch[f][c]]=f;
    ch[u][c^]=f; fa[f]=u;
    update(f); update(u);
}
//将当前节点u旋转到父亲节点

void splay(int u){
    pushdown(u);
    while(!isroot(u)){
        if(!isroot(fa[u]))
            rotate(who(fa[u])==who(u)?fa[u]:u);
        rotate(u);
    }
}
//将u旋转到当前Splay的根节点

---

4. 关键函数：　

　　$access(u)$，更改函数，把$u$到LCT根节点一路变成一条重链，同时断开一路上原来的重儿子：

　　

void access(int u){
    for(int v=;u;v=u,u=fa[u]){
        splay(u);
        ch[u][]=v;
        update(u);
    }
}

　　什么意思呢？外层for循环负责迭代从$u$一直到Splay根节点的路径，同时用$v$记录是从哪里来到$u$的。

　　每到达一个点$u$，我们将$u$提到树根，这时$u$的右儿子就是在原本重链上$u$的重儿子。我们把它替换成过来的节点，并更新信息即可。

　　$makeRoot(u)$，换根操作，使$u$成为树的根节点：

　　

void makeRoot(int u){
    access(u);
    splay(u);
    reverse(u);
}

　　换根换根，实际上影响到的是哪些因素呢？

　　仅仅是$u$到根节点一路上的Splay发生了父子反向，对于其它的Splay并没有影响。

　　于是这样调用：

1. 我们把$u$到根节点一路变为重链，即把它们放到一棵Splay中；
2. 将$u$旋转到Splay的根节点；
3. 为$u$打上翻转标记。

　　这样就为$u$到根节点的信息完成了父子反向操作。

　　

　　$link(a,b)$，连接操作，更改树形，连接a和b两个节点，即连接a和b所在的两棵LCT（前提是a和b不在同一棵LCT中）：

　　

void link(int a,int b){
    makeRoot(a);
    fa[a]=b;
}

　　我们将$a$变为$a$的LCT的根，然后将$a$的父亲设为$b$。这样就将$a$的整棵LCT连接到了$b$所在的LCT，并且$a$和$b$在定义上会相邻。

　　$cut(a,b)$，切割操作，更改树形，分离a和b两个节点，即分割出两棵独立的LCT（前提是a和b在同一棵LCT中且a和b相邻）：

　　

void cut(int a,int b){
    makeRoot(a);
    access(b);
    splay(b);
    fa[a]=;
    ch[b][]=;
    update(b);
}

　　我们将$a$变成树根，然后将$b$到树根（也就是$a$）一路变为重链，再将$b$旋转到所在Splay的根。

　　由于$a$和$b$同在一棵Splay中且$a$一定是$b$的父亲，所以Splay中$b$的左儿子一定是$a$，断开即可，记得更新，因为有了父子关系变化。

　　$isConnect(a,b)$，实现判断a和b是否在同一棵LCT中：

bool isConnect(int a,int b){
    if(a==b) return true;
    makeRoot(a);
    access(b);
    splay(b);
    return fa[a];
}

　　我们将$a$变成树根，然后将$b$到树根（也就是$a$）一路变为重链，再将$b$旋转到所在Splay的根。

　　如果$a$和$b$不在同一棵LCT中，执行$makeRoot(a)$后，$a$的父亲应该为空（$makeRoot$最后有一个$splay(u)$的操作将$u$旋转到树根）。

　　除非什么情况呢？除非a和b在同一棵LCT中，在$access(b)$并$splay(b)$后，$a$与$b$应该在同一棵Splay中，既然$b$为Splay根，那么$a$肯定不为Splay根，$a$一定有一个父亲存在。

　　至此，LCT的最常用函数已经介绍完毕，下面我们来总结一下最根本的核心思想：

　　可以发现$access(u)$和$splay(u)$总是配套出现，有时在前面配上$makeRoot$。这一套COMBO可以将$u$转到Splay树根，然后进行如同Splay一样的便捷操作。

　　 比如想求$a$到$b$的点权之和，我们可以$makeRoot(a)  +  access(b)  +  splay(b)$，此时$a$和$b$一定在同一条重链、同一棵Splay中，然后我们统计Splay中$b$和$b$的左子树的点权之和就可以了。

　　

---

总结

　　理解LCT以后就会觉得这玩意挺有意思的。一些处理信息、调用函数的思想，值得我们更多地推敲。