VIO的Bundle Adjustment推导
IMU模型和运动积分
$R_{\tiny{WB}} \left( t +\Delta{t} \right) = R_{\tiny{WB}} \left( t \right) Exp\left( \int_{t} ^{t+\Delta{t}} {}_{\tiny{B}} \omega_{\tiny{WB}} \left( \tau \right) d\tau \right)$
${}_{\tiny{W}}V \left(t+\Delta{t} \right) = {}_{\tiny{W}}V\left( t \right) + \int _{t} ^{t+\Delta{t}} {}_{\tiny{W}}a \left( \tau \right)d\tau $
${}_{\tiny{W}}P \left(t+\Delta{t} \right) = {}_{\tiny{W}}P\left( t \right) + \int _{t} ^{t+\Delta{t}} {}_{\tiny{W}}V \left( \tau \right)d\tau \,+\int \int _{t} ^{t+\Delta{t}}{}_{\tiny{W}}a \left( \tau \right)d\tau^2$
其中IMU读数,即测量值（理论值在偏置和噪声的影响下得到的读数）为
${}_{\tiny{B}} \tilde{ \omega }_{\tiny{WB}} \left( t \right) = {}_{\tiny{B}} \omega_{\tiny{WB}} \left( t \right) + b^{g} \left( t \right) +\eta^{g}\left( t \right) $
${}_{\tiny{B}} \tilde{ a } \left( t \right) = R_{\tiny{WB}}^{T} \left( t \right) \left( {}_{\tiny{W}}a\left( t \right) - {}_{\tiny{W}}g\right) + b^a\left( t \right) + \eta^a \left( t \right) $
假设在时间间隔$\left[ t,t+\Delta{t} \right]$中,${}_{\tiny{W}}a$和${}_{\tiny{B}} \omega_{\tiny{WB}}$为常数
$R_{\tiny{WB}} \left( t +\Delta{t} \right) = R_{\tiny{WB}} \left( t \right) Exp\left( {}_{\tiny{B}} \omega_{\tiny{WB}} \left( t \right) \Delta{t} \right)$
${}_{\tiny{W}}V\left( t + \Delta{t} \right) ={}_{\tiny{W}}V\left( t \right) + {}_{\tiny{W}}a \left( t \right)\Delta{t} $
${}_{\tiny{W}}P \left(t+\Delta{t} \right) = {}_{\tiny{W}}P\left( t \right)+{}_{\tiny{W}}V \left( t \right) \Delta{t} + \frac{1}{2}{}_{\tiny{W}}a \left( t \right)\Delta{t}^2$
以上的公式用IMU测量值表示：
$R \left( t +\Delta{t} \right) = R \left( t \right) Exp\left( \left( \tilde{ \omega } \left( t \right) - b^g\left( t \right) - \eta^{gd} \left( t \right) \right) \Delta{t}\right)$
$V \left( t +\Delta{t} \right) = V \left( t \right) +g\Delta{t}+R\left( t \right) \left( \tilde{ a } \left( t \right) - b^{a}\left( t \right) - \eta^{ad}\left( t \right) \right) \Delta {t}$
$P \left(t+\Delta{t} \right) = P\left( t \right) + V \left( t \right)\Delta{t} + \frac{1}{2} g\Delta{t}^2 +\frac{1}{2}R\left( t \right) \left( \tilde{ a } \left( t \right) - b^{a}\left( t \right) - \eta^{ad}\left( t \right) \right) \Delta {t}^2$
IMU预积分
给定初值，在i和j时刻对IMU的角速度和加速度进行积分，可以计算j时刻相对于i时刻的姿态：
$R_{j} = R_{i}\prod\limits_{k=i}\limits^{j-1}Exp\left( \left( \tilde{ \omega }_{k} - b^g_{k}- \eta^{gd}_{k} \right) \Delta{t} \right)$
$V_{j} = V_{i}+ g\Delta{t_{ij}}+ \sum\limits_{k=i}\limits^{j-1}R_k\left( \tilde{ a }_{k} - b^a_{k}- \eta^{ad}_{k} \right) \Delta{t}$
$P_{j} = P_{i}+ \sum\limits_{k=i}\limits^{j-1}\left[V_k\Delta{t} + \frac{1}{2}g\Delta{t}^2 + \frac{1}{2}R_k\left( \tilde{ a }_{k} - b^a_{k}- \eta^{ad}_{k} \right) \Delta{t}^2 \right]$
在preintegration理论中需要初值（$R_i$,$V_i$,$P_i$）和常数项（包含重力g的项）分离出来。
(1)
$\Delta{R_{ij}} = R_{i}^{T}R_j=\prod\limits_{k=i}\limits^{j-1}Exp\left( \left( \tilde{ \omega }_{k} - b^g_{k}- \eta^{gd}_{k} \right) \Delta{t} \right)$
$\Delta{V_{ij}} = R_{i}^{T}\left( V_j - V_i - g\Delta{t_{ij}} \right)= \sum\limits_{k=i}\limits^{j-1}\Delta{R_{ik}}\left( \tilde{ a }_{k} - b^a_{k}- \eta^{ad}_{k} \right) \Delta{t}$
$\Delta{P_{ij}} = R_{i}^{T}\left( P_j - P_i -V_i\Delta{t_{ij}}-\frac{1}{2} g\Delta{t_{ij}^2} \right)=\sum\limits_{k=i}\limits^{j-1}\left[\Delta{V_{ik}}\Delta{t}+\frac{1}{2}\Delta{R_{ik}}\left( \tilde{ a }_{k} - b^a_{k}- \eta^{ad}_{k} \right) \Delta{t}^2\right]$
其中$\Delta{R_{ij}}$,$\Delta{V_{ij}}$,$\Delta{P_{ij}}$即为preintegration measurement,即不考虑初值以及重力加速度项的相对测量。注意到这项项包含有噪声$\eta$,我们也需要将它们分离出来，在分离的过程中发现preintegration measurement是近似服从高斯分布的，即
(2)
$\Delta\tilde{R}_{ij} \approx \Delta{R_{ij}}Exp\left( \delta \phi_{ij} \right) =\prod\limits_{k=i}\limits^{j-1}Exp\left( \left( \tilde{ \omega }_{k} - b^g_{k} \right) \Delta{t} \right)$
$\Delta\tilde{V}_{ij} \approx \Delta{V_{ij}}+\delta{V_{ij}} = \sum\limits_{k=i}\limits^{j-1}\Delta{\tilde{R}_{ik}}\left( \tilde{ a }_{k} - b^a_{k} \right) \Delta{t}$
$\Delta\tilde{P}_{ij} \approx \Delta{P_{ij}}+\delta{P_{ij}}=\sum\limits_{k=i}\limits^{j-1}\left[\Delta{\tilde{V}_{ik}}\Delta{t}+\frac{1}{2}\Delta{\tilde{R}_{ik}}\left( \tilde{ a }_{k} - b^a_{k} \right) \Delta{t}^2\right]$
最终可得预积分测量模型（其中$Exp\left(-\delta\phi_{ij}\right)^T = Exp\left(\delta\phi_{ij}\right)$）
(3)
$\Delta\tilde{R}_{ij} = R_{i}^{T}R_jExp\left( \delta \phi_{ij} \right)$
$\Delta\tilde{V}_{ij} = R_{i}^{T}\left( V_j - V_i - g\Delta{t_{ij}} \right)+\delta{V_{ij}}$
$\Delta\tilde{P}_{ij} = R_{i}^{T}\left( P_j - P_i -V_i\Delta{t_{ij}}-\frac{1}{2} g\Delta{t_{ij}^2} \right)+\delta{P_{ij}}$
偏差更新
(4)
$\Delta\tilde{R}_{ij}\left( b_i^g\right) =\prod\limits_{k=i}\limits^{j-1}Exp\left( \left( \tilde{ \omega }_{k} -\bar{b}^g_{i} -\delta{b_i^g}\right) \Delta{t} \right) \simeq \Delta\tilde{R}_{ij}\left( \bar{b}_i^g\right) Exp\left(\frac{\partial\Delta\bar{R}_{ij}} {\partial{b^g}} \delta{b^g_i} \right)$
$\Delta\tilde{V}_{ij}\left( b_i^g,b_i^a \right) =\sum\limits_{k=i}\limits^{j-1}\Delta{\tilde{R}_{ik}}\left(b_i^g\right)\left( \tilde{ a }_{k} - \bar{b}^a_{i} -\delta{b}_i^a \right) \Delta{t} \simeq \Delta\tilde{V}_{ij}\left( \bar{b}_i^g,\bar{b}_i^a\right) +\frac{\partial\Delta\bar{V}_{ij}} {\partial{b^g}} \delta{b^g_i} + \frac{\partial\Delta\bar{V}_{ij}} {\partial{b^a}} \delta{b^a_i}$
$\Delta\tilde{P}_{ij}\left( b_i^g,b_i^a \right)= \sum\limits_{k=i}\limits^{j-1}\left[\Delta{\tilde{V}_{ik}}\left( b_i^g,b_i^a \right)\Delta{t}+\frac{1}{2}\Delta{\tilde{R}_{ik}}\left( b_i^g\right)\left( \tilde{ a }_{k} - \bar{b}^a_{i} -\delta{b}_i^a \right) \Delta{t}^2\right] \simeq \Delta\tilde{P}_{ij}\left( \bar{b}_i^g,\bar{b}_i^a\right) +\frac{\partial\Delta\bar{P}_{ij}} {\partial{b^g}} \delta{b^g_i} + \frac{\partial\Delta\bar{P}_{ij}} {\partial{b^a}} \delta{b^a_i}$
$\Delta\tilde{R}_{ij}\left( \bar{b}_i^g\right)$,$\Delta\tilde{V}_{ij}\left( \bar{b}_i^g,\bar{b}_i^a\right)$,$\Delta\tilde{P}_{ij}\left( \bar{b}_i^g,\bar{b}_i^a\right)$为偏置未更新的时的值，后半部分为偏置更新后的影响。
在之前的预积分推导中我们假设i和j之间的偏置是不变的(即偏置的下标为i而不是会变化的k)，但是在优化过程中偏置的估计会被一个小增量$\delta{b}$更新，将$b\gets\bar{b}+\delta{b}$代入（2）中得（4）的左半部分，对i和j之间的测量进行积分，但是这不是最高效的，所以我们采取用一阶泰勒展开的方式得（4）的右半部分,其中右半部分中的雅可比（在$\bar{b_i}$处计算所得）描述了由于估计的偏置的变化而引起的变化。
残差
$r_{\Delta{R_{ij}}} = Log\left( \left( \Delta\tilde{R}_{ij}\left( \bar{b}_i^g\right) Exp\left(\frac{\partial\Delta\bar{R}_{ij}} {\partial{b^g}} \delta{b^g} \right) \right) ^T R_i^T{R_j}\right)$
$r_{\Delta{V_{ij}}} = R_{i}^{T}\left( V_j - V_i - g\Delta{t_{ij}} \right) - \left[\Delta\tilde{V}_{ij}\left( \bar{b}_i^g,\bar{b}_i^a\right) +\frac{\partial\Delta\bar{V}_{ij}} {\partial{b^g}} \delta{b^g} + \frac{\partial\Delta\bar{V}_{ij}} {\partial{b^a}} \delta{b^a} \right]$
$r_{\Delta{P_{ij}}} = R_{i}^{T}\left( P_j - P_i -V_i\Delta{t_{ij}}-\frac{1}{2} g\Delta{t_{ij}^2} \right) - \left[ \Delta\tilde{P}_{ij}\left( \bar{b}_i^g,\bar{b}_i^a\right) +\frac{\partial\Delta\bar{P}_{ij}} {\partial{b^g}} \delta{b^g} + \frac{\partial\Delta\bar{P}_{ij}} {\partial{b^a}} \delta{b^a} \right]$
其中被减数为（1）的左半部分，减数为（4）的右半部分。
迭代噪声传播
噪声向量$\eta_{ij}^\Delta = \left[ \delta\phi^T_{ij}, \delta{V}^T_{ij},\delta{P}^T_{ij} \right]^T \sim \mathcal{N} \left( 0_{9X1},\sum_{ij} \right)$
给出递推结果：
$\delta\phi_{i,j} \backsimeq \Delta \tilde{R}_{j-1,j}^T\delta\phi_{i,j-1}+J_r^{j-1}\eta_{j-1}^{gd}\Delta{t}$
$\delta{V_{i,j}} \backsimeq \delta{V_{i,j-1}} - \Delta{\tilde{R}_{i,j-1}} \left( \tilde{a}_{j-1}-b^a_i \right)^{\wedge}\delta\phi_{i,j-1}\Delta{t}+\Delta\tilde{R}_{i,j-1}\eta_{j-1}^{ad}\Delta{t}$
$\delta{P_{i,j}} \backsimeq \delta{P_{i,j-1}} + \delta{V_{i,j-1}}\Delta{t} - \frac{1}{2}\Delta{\tilde{R}_{i,j-1}} \left( \tilde{a}_{j-1}-b^a_i \right)^{\wedge}\delta\phi_{i,j-1}\Delta{t}^2 + \frac{1}{2}\Delta\tilde{R}_{i,j-1}\eta_{j-1}^{ad}\Delta{t}^2$
写成矩阵形式：
$\begin{bmatrix}\delta\phi_{i,j} \\\delta{V}_{i,j} \\\delta{P}_{i,j}\end{bmatrix}= A_{j-1}\begin{bmatrix}\delta\phi_{i,j-1} \\\delta{V}_{i,j-1} \\\delta{P}_{i,j-1}\end{bmatrix}+B_{j-1}\eta_{j-1}^{gd}+C_{j-1}\eta_{j-1}^{ad}$这是线性模型
其中
$A_{j-1}=\begin{bmatrix} \Delta \tilde{R}_{j-1,j}^T & 0_{3X3} & 0_{3X3} \\ -\Delta{\tilde{R}_{i,j-1}} \left( \tilde{a}_{j-1}-b^a_i \right)^{\wedge}\Delta{t} & 0_{3X3} & I_{3X3} \\ - \frac{1}{2}\Delta{\tilde{R}_{i,j-1}} \left( \tilde{a}_{j-1}-b^a_i \right)^{\wedge}\Delta{t}^2 & I_{3X3} & I_{3X3}\Delta{t} \end{bmatrix}_{9X9}$
$B_{j-1} = \begin{bmatrix}J_r^{j-1}\Delta{t} \\ 0_{3X3} \\ 0_{3X3}\end{bmatrix}_{9X3}$
$C_{j-1}=\begin{bmatrix}0_{3X3} \\ \Delta\tilde{R}_{i,j-1}\Delta{t} \\ \frac{1}{2}\Delta\tilde{R}_{i,j-1} \Delta{t}^2\end{bmatrix}_{9X3}$
而写成协方差形式为：
$\sum_{ij}= A_{j-1}\sum_{i,j-1}A_{j-1}^T + B_{j-1}\eta_{j-1}^{gd}B_{j-1}^T + C_{j-1}\eta_{j-1}^{ad}C_{j-1}^T$
(4)的偏差更新中雅可比递推形式如下：
$\frac{\partial\Delta\bar{R}_{ij}}{\partial{b^g}} = -\sum^{j-1}_{k=i}\left[ \Delta\tilde{R}_{k+1,j}\left(\bar{b}_i\right)^T{J_r^k}\Delta{t}\right] $
$= -\sum^{j-1}_{k=i}\left[ \Delta\tilde{R}_{j,k+1}{J_r^k}\Delta{t}\right] $
推导：$\frac{\partial\Delta\bar{R}_{i,j+1}}{\partial{b^g}} = -\sum^{j}_{k=i}\left[ \Delta\tilde{R}_{j+1,k+1}{J_r^k}\Delta{t}\right]$
$=- \Delta{\tilde{R}_{j+1,j}}\left[ \sum_{k=i}^j \Delta{\tilde{R}_{j,k+1}}J_r^k \Delta{t}\right]$
$=- \Delta{\tilde{R}_{j+1,j}}\left[ \sum_{k=i}^{j-1} \Delta{\tilde{R}_{j,k+1}}J_r^k \Delta{t} + \Delta{\tilde{R}_{j,j+1}}J^j_r\Delta{t}\right]$
$= \Delta{\tilde{R}_{j+1,j}}\left[- \sum_{k=i}^{j-1} \Delta{\tilde{R}_{k+1,j}^T}J_r^k \Delta{t}\right]-J_r^j\Delta{t}$
$= \Delta\tilde{R}^T_{j,j+1}\frac{\partial\Delta\bar{R}_{ij}}{\partial{b^g}}-J_r^j\Delta{t}$
$\frac{\partial\Delta\bar{V}_{ij}}{\partial{b^a}} = -\sum^{j-1}_{k=i} \Delta\bar{R}_{ik}\Delta{t}$
推导：$\frac{\partial\Delta\bar{V}_{i,j+1}}{\partial{b^a}} = -\sum^{j}_{k=i} \Delta\bar{R}_{ik}\Delta{t}$
$=-\left(\Delta\bar{R}_{ij}\Delta{t} + \sum^{j-1}_{k=i} \Delta\bar{R}_{ik}\Delta{t}\right)$
$= \frac{\partial\Delta\bar{V}_{ij}}{\partial{b^a}}-\Delta\bar{R}_{ij}\Delta{t}$
$\frac{\partial\Delta\bar{V}_{ij}}{\partial{b^g}} = -\sum^{j-1}_{k=i} \Delta\bar{R}_{ik} \left(\tilde{a}_k - \bar{b}_i^a\right)^{\wedge} \frac{\partial\Delta\bar{R}_{ik}}{\partial{b^g}}\Delta{t}$
推导：$\frac{\partial\Delta\bar{V}_{i,j+1}}{\partial{b^g}} = -\sum^{j}_{k=i} \Delta\bar{R}_{ik} \left(\tilde{a}_k - \bar{b}_i^a\right)^{\wedge} \frac{\partial\Delta\bar{R}_{ik}}{\partial{b^g}}\Delta{t}$
$=-\Delta\bar{R}_{ij} \left(\tilde{a}_j - \bar{b}_i^a\right)^{\wedge} \frac{\partial\Delta\bar{R}_{ij}}{\partial{b^g}}\Delta{t}-\sum^{j-1}_{k=i} \Delta\bar{R}_{ik} \left(\tilde{a}_k - \bar{b}_i^a\right)^{\wedge} \frac{\partial\Delta\bar{R}_{ik}}{\partial{b^g}}\Delta{t}$
$= \frac{\partial\Delta\bar{V}_{ij}}{\partial{b^g}}-\Delta\bar{R}_{ij} \left(\tilde{a}_j - \bar{b}_i^a\right)^{\wedge} \frac{\partial\Delta\bar{R}_{ij}}{\partial{b^g}}\Delta{t}$
$\frac{\partial\Delta\bar{P}_{ij}}{\partial{b^a}} = \sum^{j-1}_{k=i} \frac{\partial\Delta\bar{V}_{ik}}{\partial{b^a}}\Delta{t}-\frac{1}{2}\Delta\bar{R}_{ik}\Delta{t^2} $
推导：$\frac{\partial\Delta\bar{P}_{i,j+1}}{\partial{b^a}} = \sum^{j}_{k=i} \frac{\partial\Delta\bar{V}_{ik}}{\partial{b^a}}\Delta{t}-\frac{1}{2}\Delta\bar{R}_{ik}\Delta{t^2}$
$=\frac{\partial\Delta\bar{V}_{ij}}{\partial{b^a}}\Delta{t}-\frac{1}{2}\Delta\bar{R}_{ij}\Delta{t^2}+\sum^{j-1}_{k=i} \left(\frac{\partial\Delta\bar{V}_{ik}}{\partial{b^a}}\Delta{t}-\frac{1}{2}\Delta\bar{R}_{ik}\Delta{t^2}\right)$
$= \frac{\partial\Delta\bar{P}_{ij}}{\partial{b^a}}+\left( \frac{\partial\Delta\bar{V}_{ij}}{\partial{b^a}}\Delta{t}-\frac{1}{2}\Delta\bar{R}_{ij}\Delta{t^2} \right)$
$\frac{\partial\Delta\bar{P}_{ij}}{\partial{b^g}} = \sum^{j-1}_{k=i} \frac{\partial\Delta\bar{V}_{ik}}{\partial{b^g}}\Delta{t}-\frac{1}{2}\Delta\bar{R}_{ik}\left(\tilde{a}_k - \bar{b}_i^a\right)^{\wedge} \frac{\partial\Delta\bar{R}_{ik}}{\partial{b^g}}\Delta{t}^2$
推导：$\frac{\partial\Delta\bar{P}_{i,j+1}}{\partial{b^g}} = \sum^{j}_{k=i} \left( \frac{\partial\Delta\bar{V}_{ik}}{\partial{b^g}}\Delta{t}-\frac{1}{2}\Delta\bar{R}_{ik}\left(\tilde{a}_k - \bar{b}_i^a\right)^{\wedge} \frac{\partial\Delta\bar{R}_{ik}}{\partial{b^g}}\Delta{t}^2\right)$
$=\left(\frac{\partial\Delta\bar{V}_{ij}}{\partial{b^g}}\Delta{t}-\frac{1}{2}\Delta\bar{R}_{ij}\left(\tilde{a}_j - \bar{b}_i^a\right)^{\wedge} \frac{\partial\Delta\bar{R}_{ij}}{\partial{b^g}}\Delta{t}^2\right) + \sum^{j-1}_{k=i} \left( \frac{\partial\Delta\bar{V}_{ik}}{\partial{b^g}}\Delta{t}-\frac{1}{2}\Delta\bar{R}_{ik}\left(\tilde{a}_k - \bar{b}_i^a\right)^{\wedge} \frac{\partial\Delta\bar{R}_{ik}}{\partial{b^g}}\Delta{t}^2 \right)$
$=\frac{\partial\Delta\bar{P}_{ij}}{\partial{b^g}}+ \left( \frac{\partial\Delta\bar{V}_{ij}}{\partial{b^g}}\Delta{t}-\frac{1}{2}\Delta\bar{R}_{ij}\left(\tilde{a}_j - \bar{b}_i^a\right)^{\wedge} \frac{\partial\Delta\bar{R}_{ij}}{\partial{b^g}}\Delta{t}^2 \right)$
不含噪声的递推公式
$\Delta\tilde{P}_{i,j+1} = \Delta\tilde{P}_{i,j} + \Delta\tilde{V}_{i,j}\Delta{t}+\frac{1}{2}\Delta\tilde{R}_{i,j}\left( \tilde{a}_j - \bar{b}^a_i\right)^{\wedge}\Delta{t^2}$
$\Delta\tilde{V}_{i,j+1} = \Delta\tilde{V}_{i,j}+\Delta\tilde{R}_{i,j}\left( \tilde{a}_j - \bar{b}^a_i\right)^{\wedge}\Delta{t} $
$\Delta\tilde{R}_{i,j+1} = \Delta\tilde{R}_{i,j}Exp\left[ \left( \tilde{\omega_j} - \bar{b_i^g}\right)^{\wedge}\Delta{t}\right]$
到此已经知道了delta measurements，jacobians，covariance matrix这三个部分的更新了。
// incrementally update 1)delta measurements, 2)jacobians, 3)covariance matrix
// acc: acc_measurement - bias_a, last measurement!! not current measurement
// omega: gyro_measurement - bias_g, last measurement!! not current measurement
{
void IMUPreintegrator::update(const Vector3d &omega, const Vector3d &acc, const double &dt) {
double dt2 = dt * dt; Matrix3d dR = Expmap(omega * dt);//上一次的测试
Matrix3d Jr = JacobianR(omega * dt);
// noise covariance propagation of delta measurements
// err_k+1 = A*err_k + B*err_gyro + C*err_acc
Matrix3d I3x3 = Matrix3d::Identity();
Matrix<double, , > A = Matrix<double, , >::Identity();
A.block<, >(, ) = dR.transpose();
A.block<, >(, ) = -_delta_R * skew(acc) * dt;
A.block<, >(, ) = -0.5 * _delta_R * skew(acc) * dt2;
A.block<, >(, ) = I3x3 * dt; Matrix<double, , > Bg = Matrix<double, , >::Zero();
Bg.block<, >(, ) = Jr * dt; Matrix<double, , > Ca = Matrix<double, , >::Zero();
Ca.block<, >(, ) = _delta_R * dt;
Ca.block<, >(, ) = 0.5 * _delta_R * dt2;
//协方差
_cov_P_V_Phi = A * _cov_P_V_Phi * A.transpose() +
Bg * IMUData::getGyrMeasCov() * Bg.transpose() +
Ca * IMUData::getAccMeasCov() * Ca.transpose();
// jacobian of delta measurements w.r.t bias of gyro/acc
// update P first, then V, then R
_J_P_Biasa += _J_V_Biasa * dt - 0.5 * _delta_R * dt2;
_J_P_Biasg += _J_V_Biasg * dt - 0.5 * _delta_R * skew(acc) * _J_R_Biasg * dt2;
_J_V_Biasa += -_delta_R * dt;
_J_V_Biasg += -_delta_R * skew(acc) * _J_R_Biasg * dt;
_J_R_Biasg = dR.transpose() * _J_R_Biasg - Jr * dt; // delta measurements, position/velocity/rotation(matrix)
// update P first, then V, then R. because P's update need V&R's previous state _delta_P += _delta_V * dt + 0.5 * _delta_R * acc * dt2; // P_k+1 = P_k + V_k*dt + R_k*a_k*dt*dt/2
_delta_V += _delta_R * acc * dt;
_delta_R = normalizeRotationM(_delta_R * dR); // normalize rotation, in case of numerical error accumulation
// // noise covariance propagation of delta measurements
// // err_k+1 = A*err_k + B*err_gyro + C*err_acc
// Matrix3d I3x3 = Matrix3d::Identity();
// MatrixXd A = MatrixXd::Identity(9,9);
// A.block<3,3>(6,6) = dR.transpose();
// A.block<3,3>(3,6) = -_delta_R*skew(acc)*dt;
// A.block<3,3>(0,6) = -0.5*_delta_R*skew(acc)*dt2;
// A.block<3,3>(0,3) = I3x3*dt;
// MatrixXd Bg = MatrixXd::Zero(9,3);
// Bg.block<3,3>(6,0) = Jr*dt;
// MatrixXd Ca = MatrixXd::Zero(9,3);
// Ca.block<3,3>(3,0) = _delta_R*dt;
// Ca.block<3,3>(0,0) = 0.5*_delta_R*dt2;
// _cov_P_V_Phi = A*_cov_P_V_Phi*A.transpose() +
// Bg*IMUData::getGyrMeasCov*Bg.transpose() +
// Ca*IMUData::getAccMeasCov()*Ca.transpose(); // delta time
_delta_time += dt; }
}
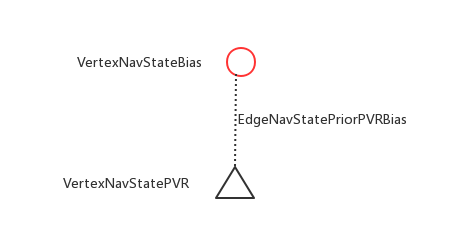
下面按照图优化的思路，建立VIO的图模型
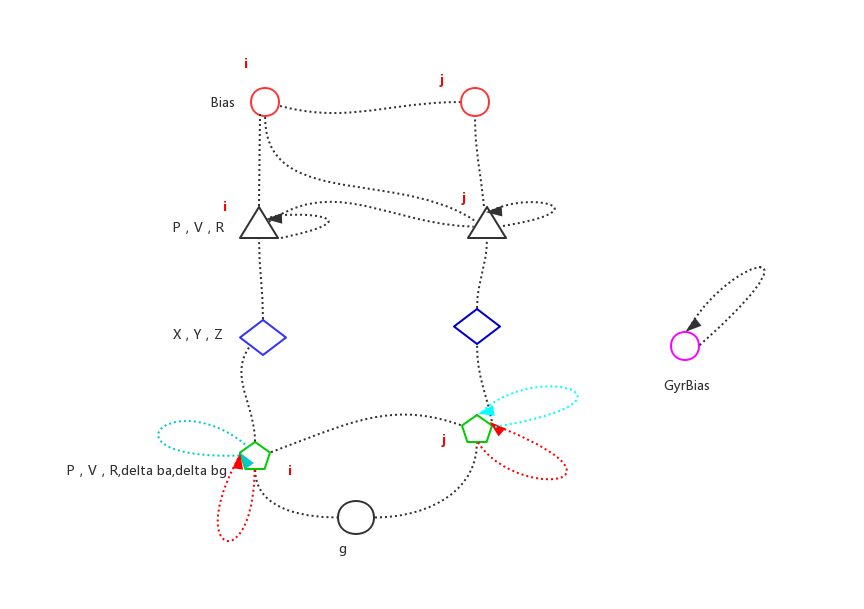
图优化的模型如上图所示。
红色圆形节点中的量为$\delta{b^a}$,$\delta{b^g}$，因为$b\gets\bar{b}+\delta{b}$，所以$\delta{b}$被优化后相当于偏置也被更新了。
三角形黑色节点的量为IMU的状态，（R,P,V）。
四边形蓝色节点的量为世界坐标下的三维点坐标，（X,Y,Z）。
青色的五边形节点的量为（R,P,V，$\delta{b^a}$，$\delta{b^g}$）
黑色的圆形节点的量为世界坐标系下的重力加速度g。
紫色的圆形节点的量为陀螺仪的偏置$b^g$
各边的误差，及雅可比计算
参考ORB-YGZ-SLAM中设置节点与边的方式
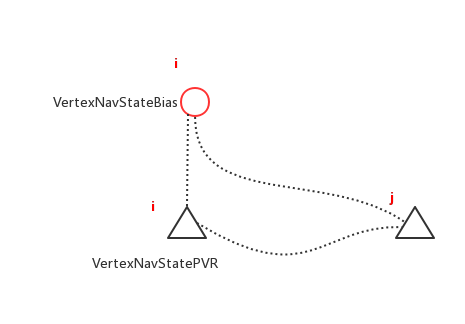
误差函数为论文【1】中公式45
$r_{\Delta{R_{ij}}} = Log\left( \left( \Delta\tilde{R}_{ij}\left( \bar{b}_i^g\right) Exp\left(\frac{\partial\Delta\bar{R}_{ij}} {\partial{b^g}} \delta{b^g} \right) \right) ^T R_i^T{R_j}\right)$
$r_{\Delta{V_{ij}}} = R_{i}^{T}\left( V_j - V_i - g\Delta{t_{ij}} \right) - \left[\Delta\tilde{V}_{ij}\left( \bar{b}_i^g,\bar{b}_i^a\right) +\frac{\partial\Delta\bar{V}_{ij}} {\partial{b^g}} \delta{b^g} + \frac{\partial\Delta\bar{V}_{ij}} {\partial{b^a}} \delta{b^a} \right]$
$r_{\Delta{P_{ij}}} = R_{i}^{T}\left( P_j - P_i -V_i\Delta{t_{ij}}-\frac{1}{2} g\Delta{t_{ij}^2} \right) - \left[ \Delta\tilde{P}_{ij}\left( \bar{b}_i^g,\bar{b}_i^a\right) +\frac{\partial\Delta\bar{P}_{ij}} {\partial{b^g}} \delta{b^g} + \frac{\partial\Delta\bar{P}_{ij}} {\partial{b^a}} \delta{b^a} \right]$
误差程序实现
void EdgeNavStatePVR::computeError() {
//
const VertexNavStatePVR *vPVRi = static_cast<const VertexNavStatePVR *>(_vertices[]);
const VertexNavStatePVR *vPVRj = static_cast<const VertexNavStatePVR *>(_vertices[]);
const VertexNavStateBias *vBiasi = static_cast<const VertexNavStateBias *>(_vertices[]);
// terms need to computer error in vertex i, except for bias error
const NavState &NSPVRi = vPVRi->estimate();
Vector3d Pi = NSPVRi.Get_P();
Vector3d Vi = NSPVRi.Get_V();
SO3d Ri = NSPVRi.Get_R();
// Bias from the bias vertex
const NavState &NSBiasi = vBiasi->estimate();
Vector3d dBgi = NSBiasi.Get_dBias_Gyr();
Vector3d dBai = NSBiasi.Get_dBias_Acc();
// terms need to computer error in vertex j, except for bias error
const NavState &NSPVRj = vPVRj->estimate();
Vector3d Pj = NSPVRj.Get_P();
Vector3d Vj = NSPVRj.Get_V();
SO3d Rj = NSPVRj.Get_R();
// IMU Preintegration measurement
const IMUPreintegrator &M = _measurement; //预积分类，实际值
double dTij = M.getDeltaTime(); // Delta Time
double dT2 = dTij * dTij;
Vector3d dPij = M.getDeltaP(); // Delta Position pre-integration measurement //测量出来的实际deltaP
Vector3d dVij = M.getDeltaV(); // Delta Velocity pre-integration measurement
Sophus::SO3d dRij = Sophus::SO3(M.getDeltaR()); // Delta Rotation pre-integration measurement
// tmp variable, transpose of Ri
Sophus::SO3d RiT = Ri.inverse();
// residual error of Delta Position measurement
Vector3d rPij = RiT * (Pj - Pi - Vi * dTij - 0.5 * GravityVec * dT2)
- (dPij + M.getJPBiasg() * dBgi +
M.getJPBiasa() * dBai); // this line includes correction term of bias change.
// residual error of Delta Velocity measurement
Vector3d rVij = RiT * (Vj - Vi - GravityVec * dTij)
- (dVij + M.getJVBiasg() * dBgi +
M.getJVBiasa() * dBai); //this line includes correction term of bias change
// residual error of Delta Rotation measurement
Sophus::SO3d dR_dbg = Sophus::SO3d::exp(M.getJRBiasg() * dBgi);
Sophus::SO3d rRij = (dRij * dR_dbg).inverse() * RiT * Rj;
Vector3d rPhiij = rRij.log();
Vector9d err; // typedef Matrix<double, D, 1> ErrorVector; ErrorVector _error; D=9
err.setZero();
// 9-Dim error vector order:
// position-velocity-rotation
// rPij - rVij - rPhiij
err.segment<>() = rPij; // position error
err.segment<>() = rVij; // velocity error
err.segment<>() = rPhiij; // rotation phi error
_error = err;
}
雅克比
对3个部分的误差$\left[r_{\Delta{P_{ij}}},r_{\Delta{V_{ij}}} , r_{\Delta{R_{ij}}}\right]$求8个部分的被优化项$\left[{P_i}, {V_i},{\phi_i},{P_j}, {V_j},{\phi_j},\tilde{\delta}b_i^g,\tilde{\delta}b_i^a\right]$的雅克比,总共24个部分。
i:
$\frac{\partial{r}_{\Delta{P_{ij}}}}{\partial\delta{P_i}} = -I_{3X1} $ , $ \frac{\partial{r}_{\Delta{V_{ij}}}}{\partial\delta{P_i}} = 0$, $ \frac{\partial{r}_{\Delta{R_{ij}}}}{\partial\delta{P_i}} = 0$
$\frac{\partial{r}_{\Delta{P_{ij}}}}{\partial\delta{V_i}} = -R_i^T\Delta{t}_{ij}$, $\frac{\partial{r}{_\Delta{V_{ij}}}}{\partial\delta{V_i}} = -R_i^T$, $\frac{\partial{r}_{\Delta{R_{ij}}}}{\partial\delta{V_i}} = 0$
$\frac{\partial{r}_{\Delta{P_{ij}}}}{\partial\delta{\phi_i}} = \left( R_i^T \left( P_j-P_i-V_i\Delta{t_{ij}}-\frac{1}{2}g\Delta{t_{ij}^2}\right)\right)^{\wedge}$, $\frac{\partial{r}_{\Delta{V_{ij}}}}{\partial\delta{\phi_i}}=\left(R_i^T\left( V_j- V_i-g\Delta{t_{ij}}\right)\right)^{\wedge}$, $\frac{\partial{r}_{\Delta{R_{ij}}}}{\partial\delta{\phi_i}} = -J_r^{-1}\left(r{}_{\Delta{R}}\left(R_i\right)\right)R^T_j{R_i}$
j:
$\frac{\partial{r}_{\Delta{P_{ij}}}}{\partial\delta{P_j}} = R_i^T{R_j}$, $\frac{\partial{r}_{\Delta{V_{ij}}}}{\partial\delta{P_j}} = 0$, $\frac{\partial{r}_{\Delta{R_{ij}}}}{\partial\delta{P_j}} = 0$
$\frac{\partial{r}_{\Delta{P_{ij}}}}{\partial\delta{V_j}} = 0$, $\frac{\partial{r}_{\Delta{V_{ij}}}}{\partial\delta{V_j}} = R_i^T$, $\frac{\partial{r}_{\Delta{R_{ij}}}}{\partial\delta{V_j}} = 0$
$\frac{\partial{r}_{\Delta{P_{ij}}}}{\partial\delta{\phi_j}} = 0$, $\frac{\partial{r}_{\Delta{V_{ij}}}}{\partial\delta{\phi_j}} = 0$, $\frac{\partial{r}_{\Delta{R_{ij}}}}{\partial\delta{\phi_j}} = J_r^{-1}\left(r{}_{\Delta{R}}\left(R_j\right)\right)$
$\tilde{\delta}{b^g_i}$,$\tilde{\delta}{b^a_i}$:
$\frac{\partial{r_{\Delta{P_{ij}}}}}{\partial\tilde{\delta}{b^g_i}}=-\frac{\partial\Delta\bar{P}_{ij}}{\partial{b_i^g}}$, $\frac{\partial{r_{\Delta{V_{ij}}}}}{\partial\tilde{\delta}{b^g_i}}=-\frac{\partial\Delta\bar{V}_{ij}}{\partial{b_i^g}}$,$\frac{\partial{r_{\Delta{R_{ij}}}}}{\partial\tilde{\delta}{b^g_i}}=\alpha$
$\frac{\partial{r_{\Delta{P_{ij}}}}}{\partial\tilde{\delta}{b^a_i}}=-\frac{\partial\Delta\bar{P}_{ij}}{\partial{b_i^a}}$, $\frac{\partial{r_{\Delta{V_{ij}}}}}{\partial\tilde{\delta}{b^a_i}}=-\frac{\partial\Delta\bar{V}_{ij}}{\partial{b_i^a}}$,$\frac{\partial{r_{\Delta{R_{ij}}}}}{\partial\tilde{\delta}{b^a_i}}=0$
其中$\alpha = -J_r^{-1}\left( r_{\Delta{R_{ij}}} \left( \delta{b}_i^g\right)\right) Exp\left( r_{\Delta{R}_{ij}}\left(\delta{b}_i^g\right)\right)^T {J}^b_r\frac{\partial\Delta\bar{R}_{ij}}{\partial{b^g}}$
雅克比程序实现
void EdgeNavStatePVR::linearizeOplus() {
//
const VertexNavStatePVR *vPVRi = static_cast<const VertexNavStatePVR *>(_vertices[]);
const VertexNavStatePVR *vPVRj = static_cast<const VertexNavStatePVR *>(_vertices[]);
const VertexNavStateBias *vBiasi = static_cast<const VertexNavStateBias *>(_vertices[]);
// terms need to computer error in vertex i, except for bias error
const NavState &NSPVRi = vPVRi->estimate();
Vector3d Pi = NSPVRi.Get_P();
Vector3d Vi = NSPVRi.Get_V();
Matrix3d Ri = NSPVRi.Get_RotMatrix();
// bias
const NavState &NSBiasi = vBiasi->estimate();
Vector3d dBgi = NSBiasi.Get_dBias_Gyr();//陀螺仪
// Vector3d dBai = NSBiasi.Get_dBias_Acc();
// terms need to computer error in vertex j, except for bias error
const NavState &NSPVRj = vPVRj->estimate();
Vector3d Pj = NSPVRj.Get_P();
Vector3d Vj = NSPVRj.Get_V();
Matrix3d Rj = NSPVRj.Get_RotMatrix();
// IMU Preintegration measurement
const IMUPreintegrator &M = _measurement;
double dTij = M.getDeltaTime(); // Delta Time
double dT2 = dTij * dTij;
// some temp variable
Matrix3d I3x3 = Matrix3d::Identity(); // I_3x3
Matrix3d O3x3 = Matrix3d::Zero(); // 0_3x3
Matrix3d RiT = Ri.transpose(); // Ri^T
Matrix3d RjT = Rj.transpose(); // Rj^T
Vector3d rPhiij = _error.segment<>(); // residual of rotation, rPhiij
Matrix3d JrInv_rPhi = Sophus::SO3::JacobianRInv(rPhiij); // inverse right jacobian of so3 term #rPhiij#
Matrix3d J_rPhi_dbg = M.getJRBiasg(); // jacobian of preintegrated rotation-angle to gyro bias i
// 1.
// increment is the same as Forster 15'RSS
// pi = pi + Ri*dpi, pj = pj + Rj*dpj
// vi = vi + dvi, vj = vj + dvj
// Ri = Ri*Exp(dphi_i), Rj = Rj*Exp(dphi_j)
// Note: the optimized bias term is the 'delta bias'
// dBgi = dBgi + dbgi_update, dBgj = dBgj + dbgj_update
// dBai = dBai + dbai_update, dBaj = dBaj + dbaj_update
// 2.
// 9-Dim error vector order in PVR:
// position-velocity-rotation
// rPij - rVij - rPhiij
// Jacobian row order:
// J_rPij_xxx
// J_rVij_xxx
// J_rPhiij_xxx
// 3.
// order in 'update_' in PVR
// Vertex_i : dPi, dVi, dPhi_i
// Vertex_j : dPj, dVj, dPhi_j
// 6-Dim error vector order in Bias:
// dBiasg_i - dBiasa_i
// 4.
// For Vertex_PVR_i
Matrix<double, , > JPVRi;
JPVRi.setZero();
// 4.1
// J_rPij_xxx_i for Vertex_PVR_i
JPVRi.block<, >(, ) = -I3x3; //J_rP_dpi
JPVRi.block<, >(, ) = -RiT * dTij; //J_rP_dvi
JPVRi.block<, >(, ) = Sophus::SO3::hat(
RiT * (Pj - Pi - Vi * dTij - 0.5 * GravityVec * dT2)); //J_rP_dPhi_i
// 4.2
// J_rVij_xxx_i for Vertex_PVR_i
JPVRi.block<, >(, ) = O3x3; //dpi
JPVRi.block<, >(, ) = -RiT; //dvi
JPVRi.block<, >(, ) = Sophus::SO3::hat(RiT * (Vj - Vi - GravityVec * dTij)); //dphi_i
// 4.3
// J_rPhiij_xxx_i for Vertex_PVR_i
Matrix3d ExprPhiijTrans = Sophus::SO3::exp(rPhiij).inverse().matrix();
Matrix3d JrBiasGCorr = Sophus::SO3::JacobianR(J_rPhi_dbg * dBgi);
JPVRi.block<, >(, ) = O3x3; //dpi
JPVRi.block<, >(, ) = O3x3; //dvi
JPVRi.block<, >(, ) = -JrInv_rPhi * RjT * Ri; //dphi_i
// 5.
// For Vertex_PVR_j
Matrix<double, , > JPVRj;
JPVRj.setZero();
// 5.1
// J_rPij_xxx_j for Vertex_PVR_j
JPVRj.block<, >(, ) = RiT * Rj; //dpj
JPVRj.block<, >(, ) = O3x3; //dvj
JPVRj.block<, >(, ) = O3x3; //dphi_j
// 5.2
// J_rVij_xxx_j for Vertex_PVR_j
JPVRj.block<, >(, ) = O3x3; //dpj
JPVRj.block<, >(, ) = RiT; //dvj
JPVRj.block<, >(, ) = O3x3; //dphi_j
// 5.3
// J_rPhiij_xxx_j for Vertex_PVR_j
JPVRj.block<, >(, ) = O3x3; //dpj
JPVRj.block<, >(, ) = O3x3; //dvj
JPVRj.block<, >(, ) = JrInv_rPhi; //dphi_j
// 6.
// For Vertex_Bias_i
Matrix<double, , > JBiasi;
JBiasi.setZero();
// 5.1
// J_rPij_xxx_j for Vertex_Bias_i
JBiasi.block<, >(, ) = -M.getJPBiasg(); //J_rP_dbgi
JBiasi.block<, >(, ) = -M.getJPBiasa(); //J_rP_dbai
// J_rVij_xxx_j for Vertex_Bias_i
JBiasi.block<, >(, ) = -M.getJVBiasg(); //dbg_i
JBiasi.block<, >(, ) = -M.getJVBiasa(); //dba_i
// J_rPhiij_xxx_j for Vertex_Bias_i
JBiasi.block<, >(, ) = -JrInv_rPhi * ExprPhiijTrans * JrBiasGCorr * J_rPhi_dbg; //dbg_i
JBiasi.block<, >(, ) = O3x3; //dba_i
// Evaluate _jacobianOplus
_jacobianOplus[] = JPVRi;
_jacobianOplus[] = JPVRj;
_jacobianOplus[] = JBiasi;
}
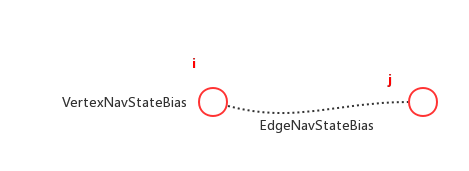
偏置误差
$r = \begin{bmatrix} \left(b_j^g+\delta b_j^g\right) - \left( b_i^g+\delta b_i^g\right) \\ \left(b_j^a+\delta b_j^a\right) - \left( b_i^a+\delta b_i^a\right) \end{bmatrix}$
误差程序实现
void EdgeNavStateBias::computeError() {
const VertexNavStateBias *vBiasi = static_cast<const VertexNavStateBias *>(_vertices[]);
const VertexNavStateBias *vBiasj = static_cast<const VertexNavStateBias *>(_vertices[]);
const NavState &NSi = vBiasi->estimate();
const NavState &NSj = vBiasj->estimate();
// residual error of Gyroscope's bias, Forster 15'RSS
Vector3d rBiasG = (NSj.Get_BiasGyr() + NSj.Get_dBias_Gyr())
- (NSi.Get_BiasGyr() + NSi.Get_dBias_Gyr());
// residual error of Accelerometer's bias, Forster 15'RSS
Vector3d rBiasA = (NSj.Get_BiasAcc() + NSj.Get_dBias_Acc()) //不是估计值与实际值之差，而是前后之差
- (NSi.Get_BiasAcc() + NSi.Get_dBias_Acc());
Vector6d err; // typedef Matrix<double, D, 1> ErrorVector; ErrorVector _error; D=6
err.setZero();
// 6-Dim error vector order: //error是六维的
// deltabiasGyr_i-deltabiasAcc_i
// rBiasGi - rBiasAi
err.segment<>() = rBiasG; // bias gyro error
err.segment<>() = rBiasA; // bias acc error
_error = err;
}
被优化项
节点i: $\left[ \delta b_i^g,\delta b_i^a\right]$,节点j: $\left[ \delta b_j^g, \delta b_j^a \right]$
偏置雅克比
$\frac{\partial r}{\partial \left[ \delta b_i^g,\delta b_i^a\right] } = \begin{bmatrix} -I_3 & 0 \\ 0 & -I_3 \end{bmatrix}$,$\frac{\partial r}{\partial \left[ \delta b_j^g,\delta b_j^a\right] } = \begin{bmatrix} I_3 & 0 \\ 0 & I_3 \end{bmatrix}$
雅克比代码实现
void EdgeNavStateBias::linearizeOplus() {
// 6-Dim error vector order:
// deltabiasGyr_i-deltabiasAcc_i
// rBiasGi - rBiasAi
_jacobianOplusXi = -Matrix<double, , >::Identity();
_jacobianOplusXj = Matrix<double, , >::Identity();
}
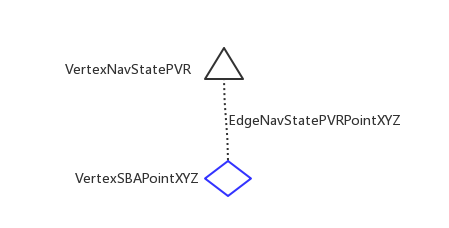
世界坐标系中空间点三维坐标经IMU坐标系转为像素二维坐标：
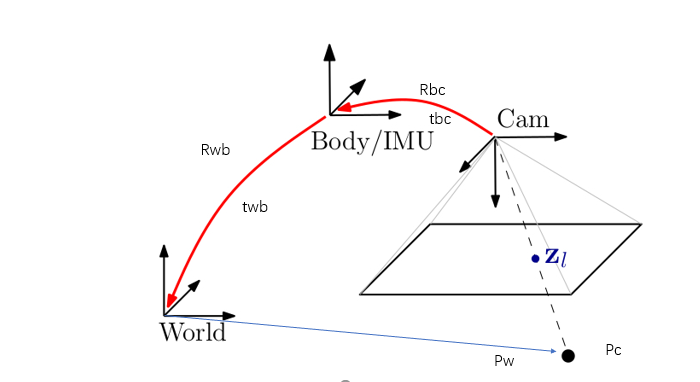
$P_b = \left(R_{bc}P_c + t_{bc}\right), P_w = \left( R_{wb}P_b + t_{wb}\right)$
$P_w = R_{wb}\left( R_{bc}P_c + t_{bc}\right) + t_{wb}$
$P_c = R_{cb}\left[ R_{wb}^T \left( P_w - t_{wb}\right) - t_{bc}\right]$
投影误差
_error = _measurement（测量值） - p(像素坐标估计值)
设$P_w = \left[ X, Y, Z\right]$,$P_c = \left[X^{'},Y^{'},Z^{'}\right]$
$p = \begin{bmatrix} u \\ v \end{bmatrix} = \begin{bmatrix} f_x\left( \frac{X^{'}}{Z^{'}}\right)+c_x \\ f_y\left( \frac{Y^{'}}{Z^{'}}\right)+c_y \end{bmatrix} $
投影误差代码实现
void computeError() {
Vector3d Pc = computePc();
Vector2d obs(_measurement);//像素坐标,实际
_error = obs - cam_project(Pc);//Pc为在相机坐标系下三维点，cam_project()将Pc转为像素坐标，误差为二维
}
bool isDepthPositive() {
Vector3d Pc = computePc();
return Pc() > 0.0;
}
Vector3d computePc() {
const VertexSBAPointXYZ *vPoint = static_cast<const VertexSBAPointXYZ *>(_vertices[]);//三维点
const VertexNavStatePVR *vNavState = static_cast<const VertexNavStatePVR *>(_vertices[]);//imu，p,v,r
const NavState &ns = vNavState->estimate();
Matrix3d Rwb = ns.Get_RotMatrix(); //矩阵形式
Vector3d Pwb = ns.Get_P();
const Vector3d &Pw = vPoint->estimate();
Matrix3d Rcb = Rbc.transpose();//相机与imu之间的关系
Vector3d Pc = Rcb * Rwb.transpose() * (Pw - Pwb) - Rcb * Pbc;
return Pc;
}
inline Vector2d project2d(const Vector3d &v) const {//相机坐标系下三维点转为均一化坐标
Vector2d res;
res() = v() / v();
res() = v() / v();
return res;
}
雅克比
优化项：$P_w$
$\frac{\partial{error}}{\partial{P_w}}=-\frac{\partial{p}}{\partial{P_w}} =-\frac{\partial{p}}{\partial{P_c}}\frac{\partial P_c}{\partial P_w} $
$\frac{\partial p}{\partial P_c} = \begin{bmatrix} f_x\frac{1}{Z^{'}} & 0 & -f_x\frac{X^{'}}{Z^{'2}} \\ 0 & f_y\frac{1}{Z^{'}} & -f_y\frac{Y^{'}}{Z^{'2}} \end{bmatrix} $, $\frac{\partial P_c}{\partial P_w} = R_{cb}R_{wb}^T$
优化项：$\left[ \delta P , \delta V , \delta R \right] = \left[ \delta P_{wb}, \delta V_{wb} , \delta R_{wb} \right] $
$ \frac{\partial{error}}{\partial{ \left[ \delta P_{wb}, \delta V_{wb} , \delta R_{wb} \right] }}=-\frac{\partial{p}}{\partial{ \left[ \delta P_{wb}, \delta V_{wb} , \delta R_{wb} \right] }} = -\frac{\partial{p}}{\partial{P_c}}\frac{\partial P_c}{\partial \left[ \delta P_{wb}, \delta V_{wb} , \delta R_{wb} \right] }$
$\frac{\partial P_c}{\partial \delta P_{wb}} = \lim_\limits{\delta P_{wb}\to 0}\frac{ R_{cb}\left[ R_{wb}^T \left( P_w - \left( P_{wb} + R_{wb}\delta P_{wb} \right) \right) - P_{bc}\right] -R_{cb}\left[ R_{wb}^T \left( P_w - P_{wb} \right) - P_{bc}\right] } {\delta P_{wb}} = -R_{cb}$, $ P_w$为世界坐标系下三维点坐标。
$\frac{\partial P_c}{\partial \delta V_{wb}} = 0$
$\frac{\partial P_c}{\partial \delta \phi_{wb}} = \lim_\limits{\delta \phi_{wb}\to 0}\frac{ R_{cb}\left[ \left( R_{wb}Exp\left( \delta \phi_{wb}^{\wedge} \right) \right)^T \left( P_w - P_{wb} \right) - P_{bc}\right] -R_{cb}\left[ R_{wb}^T \left( P_w - P_{wb} \right) - P_{bc}\right] } {\delta \phi_{wb}} = \lim_\limits{\delta \phi_{wb}\to 0}\frac{ R_{cb}\left[ \left( Exp\left( \delta \phi _{wb}^{\wedge} \right)\right)^T R_{wb}^T \left( P_w - P_{wb} \right) - P_{bc}\right] -R_{cb}\left[ R_{wb}^T \left( P_w - P_{wb} \right) - P_{bc}\right] } {\delta \phi_{wb}} $
$ = \lim_\limits{\delta \phi_{wb}\to 0}\frac{ R_{cb}\left[ \left( I - \delta \phi_{wb} ^{\wedge} \right) R_{wb}^T \left( P_w - P_{wb} \right) - P_{bc}\right] -R_{cb}\left[ R_{wb}^T \left( P_w - P_{wb} \right) - P_{bc}\right] } {\delta \phi_{wb}} = \lim_\limits{\delta \phi_{wb}\to 0}\frac{ -R_{cb}\left[ \delta \phi_{wb} ^{\wedge} R_{wb}^T \left( P_w - P_{wb} \right) \right] } {\delta \phi_{wb}}=\lim_\limits{\delta \phi_{wb}\to 0}\frac{ -R_{cb} R_{wb}^T \left( R_{wb} \delta \phi_{wb} \right)^{\wedge} \left( P_w - P_{wb} \right) } {\delta \phi_{wb}}$
$= \lim_\limits{\delta \phi_{wb}\to 0}\frac{ R_{cb} R_{wb}^T \left( P_w - P_{wb} \right) ^{\wedge} \left( R_{wb} \delta \phi_{wb} \right) } {\delta \phi_{wb}} = \lim_\limits{\delta \phi_{wb}\to 0}\frac{ \left[ R_{cb} R_{wb}^T \left( P_w - P_{wb} \right) \right] ^{\wedge} R_{cb} R_{wb}^T\left( R_{wb} \delta \phi_{wb} \right) } {\delta \phi_{wb}}$
$= \left[ R_{cb}R_{wb}^T \left(P_w-P_{wb}\right)\right]^{\wedge}R_{cb}$ 推导用到伴随矩阵的性质，和论文公式（2）
雅克比程序实现：
void EdgeNavStatePVRPointXYZ::linearizeOplus() {
const VertexSBAPointXYZ *vPoint = static_cast<const VertexSBAPointXYZ *>(_vertices[0]);
const VertexNavStatePVR *vNavState = static_cast<const VertexNavStatePVR *>(_vertices[1]);
const NavState &ns = vNavState->estimate();
Matrix3d Rwb = ns.Get_RotMatrix();
Vector3d Pwb = ns.Get_P();
const Vector3d &Pw = vPoint->estimate();
Matrix3d Rcb = Rbc.transpose();
Vector3d Pc = Rcb * Rwb.transpose() * (Pw - Pwb) - Rcb * Pbc;
double x = Pc[0];
double y = Pc[1];
double z = Pc[2];
// Jacobian of camera projection
Matrix<double, 2, 3> Maux;
Maux.setZero();
Maux(0, 0) = fx;
Maux(0, 1) = 0;
Maux(0, 2) = -x / z * fx;
Maux(1, 0) = 0;
Maux(1, 1) = fy;
Maux(1, 2) = -y / z * fy;
Matrix<double, 2, 3> Jpi = Maux / z;
// error = obs - pi( Pc )
// Pw <- Pw + dPw, for Point3D
// Rwb <- Rwb*exp(dtheta), for NavState.R
// Pwb <- Pwb + Rwb*dPwb, for NavState.P
// Jacobian of error w.r.t Pw
_jacobianOplusXi = -Jpi * Rcb * Rwb.transpose();//空间三维点对误差函数求偏导
// Jacobian of Pc/error w.r.t dPwb
Matrix<double, 2, 3> JdPwb = -Jpi * (-Rcb);//求NavState中P的偏导 ??
// Jacobian of Pc/error w.r.t dRwb
Vector3d Paux = Rcb * Rwb.transpose() * (Pw - Pwb);
Matrix<double, 2, 3> JdRwb = -Jpi * (Sophus::SO3::hat(Paux) * Rcb); // ?????
// Jacobian of Pc w.r.t NavState
// order in 'update_': dP, dV, dPhi
Matrix<double, 2, 9> JNavState = Matrix<double, 2, 9>::Zero();
JNavState.block<2, 3>(0, 0) = JdPwb;//跳过了（0.3），其实为对V求偏导，雅克比为0
JNavState.block<2, 3>(0, 6) = JdRwb;
// Jacobian of error w.r.t NavState
_jacobianOplusXj = JNavState;
}
推导同上
误差程序实现：
void computeError() {
Vector3d Pc = computePc();
Vector2d obs(_measurement);
_error = obs - cam_project(Pc);
}
bool isDepthPositive() {//是否为正深度
Vector3d Pc = computePc();
return Pc() > 0.0;
}
Vector3d computePc() {
const VertexNavStatePVR *vNSPVR = static_cast<const VertexNavStatePVR *>(_vertices[]);
const NavState &ns = vNSPVR->estimate();
Matrix3d Rwb = ns.Get_RotMatrix();
Vector3d Pwb = ns.Get_P();
//const Vector3d& Pw = vPoint->estimate();
Matrix3d Rcb = Rbc.transpose();
Vector3d Pc = Rcb * Rwb.transpose() * (Pw - Pwb) - Rcb * Pbc;
return Pc;
}
inline Vector2d project2d(const Vector3d &v) const {
Vector2d res;
res() = v() / v();
res() = v() / v();
return res;
}
Vector2d cam_project(const Vector3d &trans_xyz) const {
Vector2d proj = project2d(trans_xyz);
Vector2d res;
res[] = proj[] * fx + cx;
res[] = proj[] * fy + cy;
return res;
}
virtual void linearizeOplus();
void SetParams(const double &fx_, const double &fy_, const double &cx_, const double &cy_,
const Matrix3d &Rbc_, const Vector3d &Pbc_, const Vector3d &Pw_) {
fx = fx_;
fy = fy_;
cx = cx_;
cy = cy_;
Rbc = Rbc_;
Pbc = Pbc_;
Pw = Pw_;
}
void SetParams(const double &fx_, const double &fy_, const double &cx_, const double &cy_,
const SO3d &Rbc_, const Vector3d &Pbc_, const Vector3d &Pw_) {
fx = fx_;
fy = fy_;
cx = cx_;
cy = cy_;
Rbc = Rbc_.matrix();
Pbc = Pbc_;
Pw = Pw_; //Pw是参数？
}
protected:
// Camera intrinsics
double fx, fy, cx, cy;
// Camera-IMU extrinsics
Matrix3d Rbc;
Vector3d Pbc;
// Point position in world frame
Vector3d Pw;
};
雅克比程序实现：
void EdgeNavStatePVRPointXYZOnlyPose::linearizeOplus() {
const VertexNavStatePVR *vNSPVR = static_cast<const VertexNavStatePVR *>(_vertices[]);
const NavState &ns = vNSPVR->estimate();
Matrix3d Rwb = ns.Get_RotMatrix();
Vector3d Pwb = ns.Get_P();
Matrix3d Rcb = Rbc.transpose();
Vector3d Pc = Rcb * Rwb.transpose() * (Pw - Pwb) - Rcb * Pbc;
double x = Pc[];
double y = Pc[];
double z = Pc[];
// Jacobian of camera projection
Matrix<double, , > Maux;
Maux.setZero();
Maux(, ) = fx;
Maux(, ) = ;
Maux(, ) = -x / z * fx;
Maux(, ) = ;
Maux(, ) = fy;
Maux(, ) = -y / z * fy;
Matrix<double, , > Jpi = Maux / z;
// error = obs - pi( Pc )
// Pw <- Pw + dPw, for Point3D
// Rwb <- Rwb*exp(dtheta), for NavState.R
// Pwb <- Pwb + Rwb*dPwb, for NavState.P
// Jacobian of Pc/error w.r.t dPwb
//Matrix3d J_Pc_dPwb = -Rcb;
Matrix<double, , > JdPwb = -Jpi * (-Rcb); //????????????
// Jacobian of Pc/error w.r.t dRwb
Vector3d Paux = Rcb * Rwb.transpose() * (Pw - Pwb);
Matrix<double, , > JdRwb = -Jpi * (Sophus::SO3::hat(Paux) * Rcb); //??????????????
// Jacobian of Pc w.r.t NavStatePVR
// order in 'update_': dP, dV, dPhi
Matrix<double, , > JNavState = Matrix<double, , >::Zero();
JNavState.block<, >(, ) = JdPwb;
JNavState.block<, >(, ) = JdRwb;
// Jacobian of error w.r.t NavStatePVR
_jacobianOplusXi = JNavState;
}
不好意思，烂尾了，欢迎交流
参考论文
[1]Christian Forster, Luca Carlone, Frank Dellaert, Davide Scaramuzza,“On-Manifold Preintegration for Real-Time Visual-Inertial Odometry”,in IEEE Transactions on Robotics, 2016.
VIO的Bundle Adjustment推导的更多相关文章
- bundle adjustment 玩具程序
结合 bundle adjustment原理(1) 和 Levenberg-Marquardt 的 MATLAB 代码 两篇博客的成果,调用MATLAB R2016a中 bundleAdjustmen ...
- bundle adjustment原理(1)
那些光束平差的工具,比如SBA.SSBA之类的虽然好,然而例子和教程都不够多且不够详细,让初学者难以上手. 要传入的参数虽然有解释,然而却也不是十分清楚其含义,具体要怎么生成,生成为什么形式. 我在折 ...
- bundle adjustment原理(1)转载
转自菠菜僵尸 http://www.cnblogs.com/shepherd2015/p/5848430.html bundle adjustment原理(1) 那些光束平差的工具,比如SBA.SSB ...
- 机器人学 —— 机器人视觉（Bundle Adjustment）
今天完成了机器人视觉的所有课程以及作业,确实是受益匪浅啊! 最后一个话题是Bundle Adjustment. 机器人视觉学中,最顶尖的方法. 1.基于非线性优化的相机位姿估计 之前已经在拟合一篇中, ...
- Bundle Adjustment光束平差法概述
http://blog.csdn.net/abcjennifer/article/details/7588865 http://blog.csdn.net/ximenchuixuezijin/arti ...
- Bundle Adjustment---即最小化重投影误差（高翔slam---第七讲）
一.历史由来 Adjustment computation最早是由geodesy的人搞出来的.19世纪中期的时候,geodetics的学者就开始研究large scale triangulations ...
- 如何从零开始系统化学习视觉SLAM？
由于显示格式问题,建议阅读原文:如何从零开始系统化学习视觉SLAM? 什么是SLAM? SLAM是 Simultaneous Localization And Mapping的 英文首字母组合,一般翻 ...
- 当前的开源SLAM方案
开源方案 传感器形式 地址链接 MonoSLAM 单目 https://github.com/hanmekim/SceneLib2 PTAM 单目 http://www.robots.ox.ac. ...
- SLAM的现在与未来
http://geek.csdn.net/news/detail/202128 作者:高翔,张涛,刘毅,颜沁睿. 编者按:本文节选自图书<视觉SLAM十四讲:从理论到实践>,系统介绍了视觉 ...
随机推荐
- mysql 删除死锁的事务
select * from information_schema.innodb_trxkill 953
- MYSQL TIMESTAMP with implicit DEFAULT value is deprecated.
TIMESTAMP with implicit DEFAULT value is deprecated. Please use --explicit_defaults_for_timestamp se ...
- NBU 还原windows ORACLE数据库(FP)
二.基于差异备份恢复7月20日星期四早上8:30分数据1.查询所需要的归档日志(因为要返回20号刂8:30分的数据,所以控制 文件要晚于这个点,即取21号凌晨2点备份的控制文件) bplist -C ...
- ADT下载地址整理（转）
转自: http://blog.csdn.net/xqf222/article/details/9821971 参考下面文章 http://developer.android.com/tools/sd ...
- 79. Word Search (Array; DFS,Back-Track)
Given a 2D board and a word, find if the word exists in the grid. The word can be constructed from l ...
- Qt Image Water Marker
QString str = "input.jpg"; if(!img.load(str)){ return; } QImage mark(img.width()/2,img.hei ...
- A simple way to crack VBA password in Excel file
Unbelivibale, but I found a very simple way that really works! Do the follwoing: 1. Create a new sim ...
- Python之模块和包学习
模块简介 python是由一系列的模块组成的,每个模块就是一个py为后缀的文件,同时模块也是一个命名空间,从而避免了变量名称冲突的问题.模块我们就可以理解为lib库,如果需要使用某个模块中的函数或对象 ...
- Swift：使用CAShapeLayer打造一个ProgresssBar
ProgressBar是一个很小却在很多地方都会用到的东西.也许是网络连接,也许APP本身有很多东西需要加载的.默认的只有一个旋转的菊花,对于打造一款个性的APP这显然是不够的.这里就使用CAShap ...
- mybatis 教程
地址: http://blog.csdn.net/techbirds_bao/article/details/9233599/