Data_Structure01-绪论

---恢复内容开始---

一.作业题目

仿照三元组或复数的抽象数据类型写出有理数抽象数据类型的描述 （有理数是其分子、分母均为整数且分母不为零的分数）。
有理数基本运算：

1. 构造有理数T，元素e1,e2分别被赋以分子、分母值
2. 销毁有理数T
3. 用e(引用类型参数)返回有理数T的分子或分母,当入参i为1时返回分子, i为2是返回分母。
4. 将有理数T的分子或分母更改为e,入参i为1时改变分子, i为2是改变分母
5. 有理数T1,T2相加,结果存入有理数T3
6. 有理数T1,T2相减,结果存入有理数T3
7. 有理数T1,T2相乘,结果存入有理数T3
8. 有理数T1,T2相除,结果存入有理数T3
   实验要求：
9. 抽象数据类型名为Rational。
10. 有理数分母不能为负数或者0，类似输入请提示重输入。
11. 数据对象和数据运算的表示与数据操作的实现分离。表示用头文件完成，实现用CPP文件完成。Main.cpp文件实现数据输入输出。
12. 数据输入输出格式参考如下：
    输入：
    1 3 //T1的分子、分母
    1 2 //T2的分子、分母
    ** 输出：**
        5 6  //两个有理数相加
        -1 6  //两个有理数相减
         1 6  //两个有理数相乘
         2 3  //两个有理数相除
13. 程序应对异常输入或者出错必要处理和提示，比如提示：“分数是否需要约分等”。

二.作业内容

1.用ADT的抽象数据模型描述我的有理数数据类型。

ADT Rational{

                    数据对象：D={ e1, e2 | e1,e2属于ElemType类型} 

                    数据关系：R={<e1,e2>|e1是有理数的分子部分，e2是有理数的分母部分,且e2不等于0}

                    基本运算：

                           AssignRational(&T,v1,v2):构造有理数T，元素v1,v2分别被赋以分子、分母值

DestoryRational(&T):销毁有理数T

ReturnT(i,e,&T):操作结果:返回有理数T的分子或分母，当入参i为1时返回分子，入参i为2时返回分母

                           ChangeT(i,e,&T)：操作结果:将有理数T的分子或分母更改为e，当入参i为1时改变分子，入参i为2时改变分母

                           Add(T1,T2,&T3):有理数T1,T2相加,结果存入有理数T3

                           Subtract(T1,T2,&T3):有理数T1,T2相减,结果存入有理数T3

                           Multiply(T1,T2,&T3):有理数T1,T2相乘,结果存入有理数T3

                           Divide(T1,T2,&T3):有理数T1,T2相除,结果存入有理数T3

}ADT Rational

2.数据结构、函数说明

头文件：

函数：

 

3.代码实现说明：

e1,e2是T1的分子分母；e3,e4是T2的分子分母

（1） 有理数相加

（2） 有理数相减

（3） 有理数相乘

（4） 有理数相除

（5）约分

4.结果展示：

1.正常情况

2.分母为零

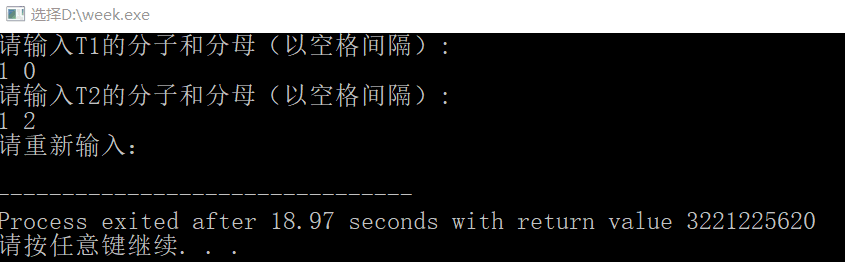
三.作业反思

对于数据的正负数，能否约分要做进一步的处理；否则最终结果会错误；并且知道了抽象数据类型把问题分解为多个规模较小且容易处理的问题，然后把每个功能模块的实现为一个独立单元，通过一次或多次调用来实现整个问题。

---恢复内容结束---