二进制补码除法——计算机底层整数除法模拟之Java实现

前面讲到布思算法的计算机底层模拟的时候，我们是借助于一个可以储存、表示任意N位的二进制补码的BinaryQueue实现的，现在我们模拟计算机底层整数除法还是要借助于它：

BinaryQueue类代码：https://www.cnblogs.com/XT-xutao/p/10050518.html

我又写了一个只基于二进制字符串的，更简单，更方便

现在考虑计算机底层除法是怎样实现的。

对于我们人工计算来说是比较简单的，从高位一直到低位，一次次除，得出每一位的商，最后剩下余数即可。

计算机似乎也可以运用这种方式：

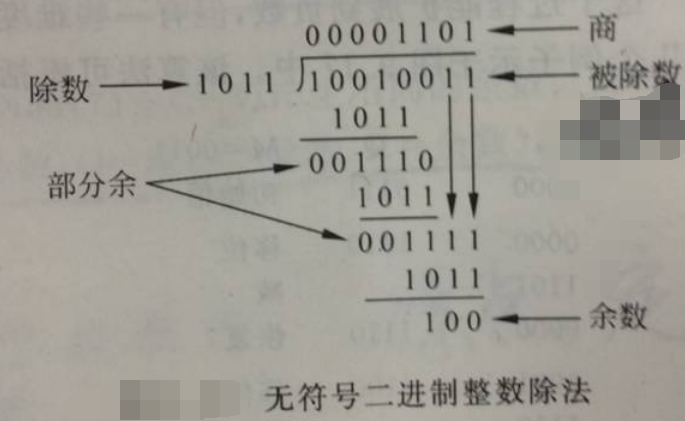
不过这只是无符号二进制整数，要是补码形式的整数呢？

似乎是不可取的，因为如果被除数是负数，那么他前面的一系列 1 是不能作为判断依据得出每一位的商的。

那么，怎么办？

在计算机底层中，我们在ALU中利用几个寄存器就可以搞定。

*  M: 除数
*  Q：被除数，被除数必须从N为算术扩展为2N位，但扩展为不存于Q中
*  A：由于被除数需要扩展，我们用A来实现扩展位，
*     初始化： 若Q 大于等于0，初始化为0，即0...0
*             若Q小于0,则初始化为-1，即1...1
*  Q0: Q最低位

除法定义如下：

     被除数 = 除数 X 商 + 余数；（余数有正负）
于是我们有如下计算步骤：

*  1.A,Q左移一位
*  2.判断：M 与 A
*      同号：A = A-M
*      异号：A = A+M
*  3.判断：
*      A未变号 或 A=0：Q0 = 1
*      A变号 且 A！=0：Q0 = 0，A 恢复值
*  4.重复 1-3 步N次
*  5.余数在A中
*      判断：被除数与除数
*        同号：商在Q中
*        异号：商为Q中取负数

于是可以有如下Java实现：

   //直接用字符串形式，其他的一些方法是基于ALU，或者是其扩展，都易于实现的。
     public String[] divide(String a, String b) { // a/b
         String A = get01(a.length(), a.substring(0, 1));//附加寄存器，存放Q的扩展位，初始化为等位的被除数左扩位（1/0）
         String Q =  a; //被除数算术左扩为2n然后存到寄存器Q,注意A就是扩展位，扩展位不存在Q中，即AQM三个都等长
         String M = b;//除数放到寄存器M
         for (int i = 0; i < a.length(); i++) {
             char A_sign = A.charAt(0);

             //A Q 左移1位
             String temp = shiftLeft(A + Q);
             A = temp.substring(0, a.length());
             Q = temp.substring(a.length());

             //判断ＭＡ是否同号
             if (M.charAt(0) == A.charAt(0)) {// A M has same sign
                 A = substract(A, M).substring(1);
             }
             else {
                 A = add(A, M).substring(1);
             }

             //判断A的符号变化没有；
             if (A_sign == A.charAt(0) || !A.contains("1")) {//A符号没变，或者A=0（不含“1”即全0）；
                 Q = Q.substring(0, Q.length() - 1) + "1"; //Q0=1
             }
             else {//A的符号变了，且A!=0
                 Q = Q.substring(0, Q.length() - 1) + "0"; //Q0=0
                 A = add(A, M).substring(1); //A =A+M 恢复;
             }
         }
         String[] res = new String[2]; //返回0：商，1：余数
         res[0] = (a.charAt(0) == b.charAt(0)) ? Q : getNegative(Q);
         res[1] = A;
         return res;
     }

 //用BinaryQueue

   public class Division {
     private BinaryQueue A,M ,Q;
     private int len ;
     private int n1,n2;
     public Division(String dividend, String divisor){ // 假设是同样长度的，如果不同长度再扩展
         len = dividend.length();//位长度
         boolean isSameSign = dividend.charAt(0)==divisor.charAt(0);
         M = new BinaryQueue(divisor);//除数
         Q = new BinaryQueue(dividend);//被除数

         n1 = Q.getInt();//被除数
         n2 = M.getInt();//除数

         //初始化A为Q的扩展位
         if (dividend.charAt(0)=='1') {// Q<=0
             String ss="";
             for (int i =0;i<len;i++ )ss+="1";
             A = new BinaryQueue(ss);
         }
         else A = new BinaryQueue(len);

         System.out.println(A.getStr()+ " "+ Q.getStr()+" "+M.getStr()+" 初始化");

         for (int i =0;i<len;i++){
             int a = A.getFirst();//提取A的最高位，一边步骤3判断A是否变号
             boolean isAddation = false;// 记录步骤2中是加操作还是减，以便步骤三恢复A的数值
 　　　　　　　　//步骤1
              A.shiftLeft();
                A.set(len-1,Q.get(0));
              Q.shiftLeft();
 　　　　　　　　//步骤2
              if (A.getFirst()==M.getFirst()){
                  A = A.subtract(M);
              }
              else {
                  A = A.add(M);
                  isAddation = true;
              }
             // 步骤3
              if (A.isZero()||a==A.getFirst()) {
                  Q.set(len-1,1);
              }
              else {
                  Q.set(len-1,0);
                  if (isAddation) A = A.subtract(M);
                  else A = A.add(M);
              }
             System.out.println(A.getStr()+ " "+ Q.getStr()+" "+M.getStr()+" 第"+i+"周期");
         }

         System.out.println(n1+"/"+n2 +" = "+ (isSameSign?Q.getInt():Q.getOppositeNumber().getInt())+"···"+A.getInt());

     }

     public static void main(String[] args) {
         new Division("10000","00011");

         new Division("0110111010","0001000101");
         new Division("1000001010","1111100101"); 

  } 
}

Demo：
A    Q     M

11111 10000 00011 初始化
11111 00000 00011 第0周期
11110 00000 00011 第1周期
11111 00001 00011 第2周期
11110 00010 00011 第3周期
11111 00101 00011 第4周期
-16/3 = -5···-1

0000000000 0110111010 0001000101 初始化
0000000000 1101110100 0001000101 第0周期
0000000001 1011101000 0001000101 第1周期
0000000011 0111010000 0001000101 第2周期
0000000110 1110100000 0001000101 第3周期
0000001101 1101000000 0001000101 第4周期
0000011011 1010000000 0001000101 第5周期
0000110111 0100000000 0001000101 第6周期
0000101001 1000000001 0001000101 第7周期
0000001110 0000000011 0001000101 第8周期
0000011100 0000000110 0001000101 第9周期
442/69 = 6···28

1111111111 1000001010 1111100101 初始化
1111111111 0000010100 1111100101 第0周期
1111111110 0000101000 1111100101 第1周期
1111111100 0001010000 1111100101 第2周期
1111111000 0010100000 1111100101 第3周期
1111110000 0101000000 1111100101 第4周期
1111111011 1010000001 1111100101 第5周期
1111110111 0100000010 1111100101 第6周期
1111101110 1000000100 1111100101 第7周期
1111111000 0000001001 1111100101 第8周期
1111110000 0000010010 1111100101 第9周期
-502/-27 = 18···-16