大白话5分钟带你走进人工智能-第十五节L1和L2正则几何解释和Ridge，Lasso，Elastic Net回归

第十五节L1和L2正则几何解释和Ridge，Lasso，Elastic Net回归

上一节中我们讲解了L1和L2正则的概念，知道了L1和L2都会使不重要的维度权重下降得多，重要的维度权重下降得少，引入L1正则会使不重要的w趋于0（达到稀疏编码的目的），引入L2正则会使w的绝对值普遍变小（达到权值衰减的目的）。本节的话我们从几何角度再讲解下L1和L2正则的区别。

L1正则是什么？|W1|+|W2|，假如|W1|+|W2|=1，也就是w1和w2的绝对值之和为1 。让你画|W1|+|W2|=1的图形，刚好是下图中方形的线。

​

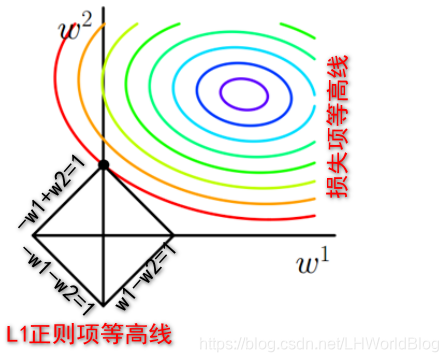
仔细思考一下，用一个分类函数去讨论，比如第二象限，W1小于零，W2大于零，此时这个绝对值就等于W2-W1=1，在第一象限里面，它俩都大于零，就把绝对值脱掉，变成W1+W2=1，所以，这是一个分类讨论的例子。所以根据4个象限的取值不同，画出图中所示的L1正则项等高线的图。

L2正则是什么？，画出其图形刚好是个圆形。

​

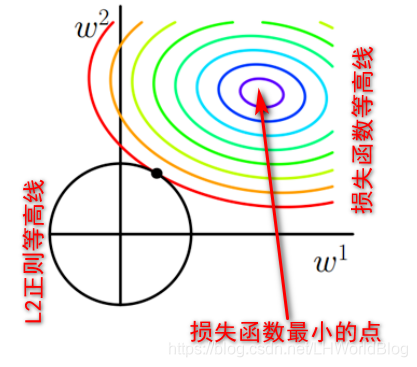
无论是L1正则还是L2正则，最后的最优解一定是出现在损失函数和正则等高线的焦点上。为什么呢，我们反推一下，如果不在焦点，假如说这是一个二维空间，这个例子里面有两个W，假如不加正则，能够使损失函数达到最小值的点也就是目标函数最优解的地方，如果加上了L1正则或者L2正则，原来只使损失函数达到最小值的地方，还能使目标函数达到最小值吗？ 肯定不能，那么最优解得点它在哪？

假设新的最优点在下图位置：

​

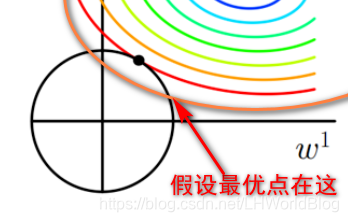
因为圆圈是L2正则的等高线，所以L2没变小，谁变大了，损失项是不是变大了？因为损失函数等高线越往外值越大，所以上图中这个假设的最优点的损失项，肯定比焦点上的损失项要大。

假设新的最优点在下图位置：

​

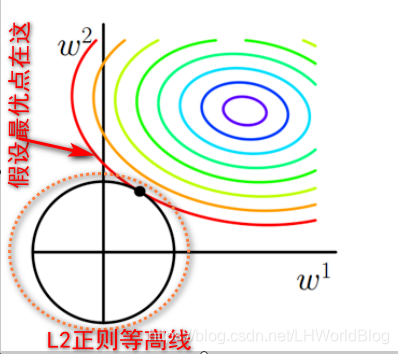
虽然损失项没变大，但是这个正则项是不是变大了？所以最优解一定会出现在它们的相切的位置，也就是焦点的位置。

又因为L1正则的等高线图形是这种方形的，所以最优解更容易出现在轴上。

​

此时W1=0，W2=1。这个图在很多书里面都出现过。但是特别讨厌的就是没有一本书给你解释这个图是怎么个意思？实际上方形和圆形是L1，L2正则的等高线。 而这些彩色的圆圈是loss的等高线，它想解释的是为什么L1正则更容易导致某些W变为零，本质上是因为它在空间里面形成的等高线是尖的，在轴上它会扎到loss的等高线上，而这个圆乎乎的东西L2正则的等高线它不会扎。所以L2正则你再怎么加，再不重要的特征，也不会让它到零。这个是由它的几何特性决定的，L2它就是一个圆乎乎的东西，L1是一个很尖锐的东西。

接下来我们讨论下Ridge回归与Lasso回归，  Ridge回归（岭回归）的公式如下：

                                                                         

你发现它就是一个线性回归，加了一个L2正则。再来看下 Lasso回归，它就是一个线性回归，加了一个L1正则。

α是什么？α是取决于你有多重视正则项，也就是多重视模型简单程度的，值越大，说明我越想得到简单的模型。假如你把α调成了很大比如100，就证明我只想要一个简单的模型，模型错的多离谱，我并不在乎。假如我们调成了一个0.01，可能简单性我不是那么重视，也重视。但是模型一定得相对做好。所以α一般会调到多大？是大于1还是小于1的？一定是小于1的。默认α通常会0.1，0.01，也可以是0.001。

我们再看下面关于α的变化与W的对应变化的图：

​

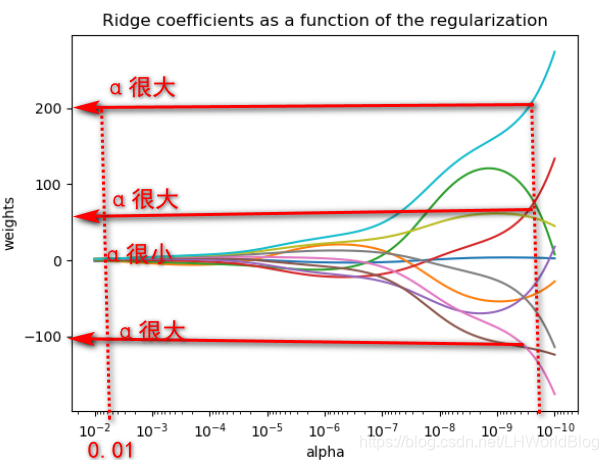
这十条线代表10个W，当这个α调到10的-10次方的时候，几乎你可以认为它压根就没加L2正则。这会L2正则影响极小的时候，你发现此时模型训练出来的W都是一个特别大的权重的模型(200,150,-100等)，因为它只追求了损失函数一定要最低。但你看随着把α的权重越调越大的话，这些线都迅速地被收起来了。仅仅将α调到0.01的时候，此时W就变得很小了，你可以想象α的系数才0.01，因此也不会对错误率影响很大。当然这个例子一定是一个特殊情况，现实情况可能不会那么完美，它不一定会有这么大作用。但是你可以看到哪怕你α只设了一点点，就比不设强很多，它就能大幅度的简化掉你模型原来没有用的大权重，与此同时又没带来太高的错误率，没带来太高的损失，所以通常都会加L2正则。。

Ridge回归（岭回归）和Lasso回归两种方式的结合，叫Elastic Net，也就是对损失函数同时增加L1和L2正则。公式如下：

                                          

  α是超参数，  ρ是一个新的超参数，它是一个0到1之间的数，当ρ值为0的时候， L1正则就被干掉了。当ρ值为1的时候，L2正则被干掉了，当ρ值为0.5或0.6，0.7的时候，就变成了一个两种正则的混合形式，它兼备了L1跟L2两项特点。那么底下这张图解释下Elastic Net与Lasso回归的对比:

​

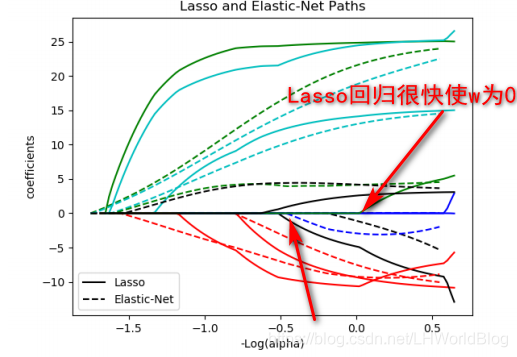
实线为什么是岭回归，因为随着α增大，w归到0上去了。所以加的是L1正则，L1正则会使W为0，因L2正则它都不着急归为零，但都会使w通通变小，所以你加了L1正则的时候w迅速的缩到0了。Elastic Net它也能让这个w缩进去，但它缩的比原来晚了一些。比如原来这个蓝线Lasso回归很快使w变为0,很快缩到0，而Elastic Net相对很慢才使w变为0，缩的较慢。实际上它的应用不是特别多，为什么不是特别多？因为超参数不好调，你永远找不到一个最合适的ρ，来平衡他们的关系，并且还能说明白了为什么你要选这个ρ。如果你说那我就成败论英雄，我就试哪个ρ对训练集最好，我就选哪个ρ，这本身是不是就是一种过拟合，就相当于你去迎合你的训练集的概念上去了。