时间序列算法（平稳时间序列模型，AR(p),MA(q),ARMA(p,q)模型和非平稳时间序列模型，ARIMA(p,d,q)模型）的模型以及需要的概念基础学习笔记梳理

在做很多与时间序列有关的预测时，比如股票预测，餐厅菜品销量预测时常常会用到时间序列算法，之前在学习这方面的知识时发现这方面的知识讲解不多，所以自己对时间序列算法中的常用概念和模型进行梳理总结（但是为了内容的正确性有些内容我通过截图来记录吧），希望能有所帮助^.^

一、时间序列的预处理

在拿到基于时间的观测值序列后，需要首先进行两步预处理，一个是纯随机性检验，另一个是平稳性检验，然后根据这两步的检验结果再采取相应的时间序列模型进行分析。

简单来讲平稳序列就是指均值和方差不发生明显变化

注：时序图检验和自相关检验实际是通过绘制相应的图进行观察，在下面的内容会结合具体的图进行分析

二、平稳时间序列模型

在学习具体模型之前，我们需要了解两种相关系数

1.自相关系数

2.偏相关系数

不要小看这两个系数，它们对于模型的选择起着至关重要的作用，如果现在对这两个系数还不是很理解，请继续往下看吧~。~

（一）、自回归模型AR(p)

（二）、移动平均模型MA(q)

(三）、自回归移动平均模型ARMA(p,q)

三、非平稳时间序列模型

在实际环境中大多数序列都是非平稳的，这里主要学习ARIMA模型

从它的名字我们就可以看到在使用它时需要首先对数据进行差分运算将非平稳时间序列变为平稳时间序列，然后再运用ARIMA模型。

四、确定参数p,q的取值

现在还剩最后一个问题要解决了，我们已经知道时间序列都有哪些模型了，那么我们怎么确定使用哪个模型呢，确定了使用哪个模型后，就要特别注意我用绿色圈圈画出的p,q，怎么确定相应模型的参数取值呢？

让我们看一下下面的这张图吧，它就是上面两个问题的key，现在直接看肯定是看不明白的，让我们先看列ACF,PACF，它们其实就是自相关系数和偏自相关系数（在上面已经提到了）的图，先知道一下什么是截尾的概念，截尾就是指ACF图，PACF图何时落入置信区间（这个是我自己理解的，大家可以自行查阅）

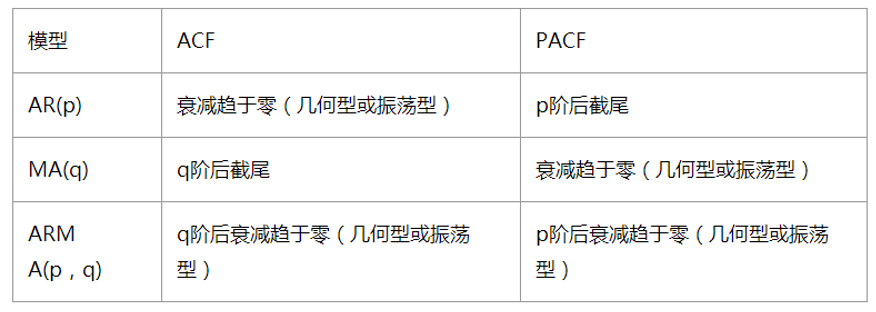
确定参数p,q的取值主要有两种方法：

1.肉眼观察ACF图和PACF图法

现在我们结合上面的原则观察下面的自相关图和偏自相关图，发现自相关图1阶截尾，偏自相关图具有拖尾性，所以可以确定为MA模型，并且取q为1，但是有时观察图并不是很准确，我们就可以使用下面的方法啦

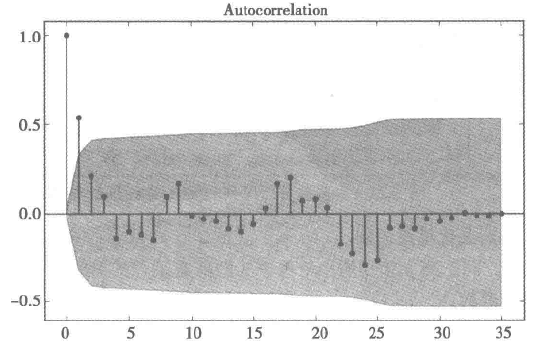
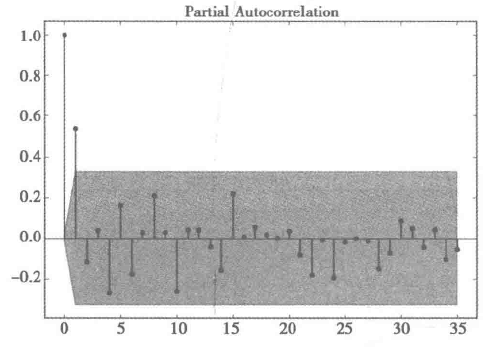
2.计算AIC,BIC,原则是使AIC和BIC越小越好（大家可以自己查阅具体详细的知识^.^)

终于写完这篇梳理笔记了，开心。