Python开发——排队问题随机模拟分析

案例:主要是基于“蒙特卡罗思想”，求解排队等待时间问题

场景：厕所排队问题

1、两场电影结束时间相隔较长，互不影响；

2、每场电影结束之后会有20个人想上厕所；

3、这20个人会在0到10分钟之内全部到达厕所；

4、每个人上厕所时间在1-3分钟之间

首先模拟最简单的情况，也就是厕所只有一个位置，不考虑两人共用的情况则每人必须等上一人出恭完毕方可进行。

分析：对于每个人都有如下几个参数：

到达时间 / 等待时间 / 开始上厕所时间 / 结束时间

#!/usr/bin/env python
# -*- coding:utf-8 -*-
# Author:Dang

'''
Part1  设置随机值
'''
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import seaborn as sns

arrivingtime = np.random.uniform(0,10,size = 20)
arrivingtime.sort()
workingtime = np.random.uniform(1,3,size = 20)
# np.random.uniform 随机数：均匀分布的样本值

startingtime = [0 for i in range(20)]
finishtime = [0 for i in range(20)]
waitingtime = [0 for i in range(20)]
emptytime = [0 for i in range(20)]
# 开始时间都是0
print('arrivingtime\n',arrivingtime,'\n')
print('workingtime\n',workingtime,'\n')
print('startingtime\n',startingtime,'\n')
print('finishtime\n',finishtime,'\n')
print('waitingtime\n',waitingtime,'\n')
print('emptytime\n',emptytime,'\n')

'''
Part2  第一人上厕所时间
'''
startingtime[0] = arrivingtime[0]
# 第一个人之前没有人，所以开始时间 = 到达时间
finishtime[0] = startingtime[0] + workingtime[0]
# 第一个人完成时间 = 开始时间 + “工作”时间
waitingtime[0] = startingtime[0]-arrivingtime[0]
# 第一个人不用等待
print(startingtime[0])
print(finishtime[0])
print(waitingtime[0])

'''
Part3  第二人之后
'''
for i in range(1,len(arrivingtime)):
    if finishtime[i-1] > arrivingtime[i]:
        startingtime[i] = finishtime[i-1]
    else:
        startingtime[i] = arrivingtime[i]
        emptytime[i] = arrivingtime[i] - finishtime[i-1]
    # 判断：如果下一个人在上一个人完成之前到达，则 开始时间 = 上一个人完成时间，
    # 否则 开始时间 = 到达时间，且存在空闲时间 = 到达时间 - 上一个人完成时间
    finishtime[i] = startingtime[i] + workingtime[i]
    waitingtime[i] = startingtime[i] - arrivingtime[i]
    print('第%d个人：到达时间 开始时间 “工作”时间 完成时间 等待时间\n' %i,
          arrivingtime[i],
          startingtime[i],
          workingtime[i],
          finishtime[i],
          waitingtime[i],
         '\n')

print('arerage waiting time is %f' %np.mean(waitingtime))

"""
数据统计
"""
sns.set(style = 'ticks',context = "notebook")
fig = plt.figure(figsize = (8,6))
arrivingtime, = plt.plot(arrivingtime,label = 'arrivingtime')
startingtime, = plt.plot(startingtime,label = 'startingtime')
workingtime, = plt.plot(workingtime,label = 'workingtime')
finishtime, = plt.plot(finishtime,label = 'finishtime')
waitingtime, = plt.plot(waitingtime,label = 'waitingtime')

plt.title(("Queuing problem random simulation experiment").title())

plt.xlabel("Arriving Time(min)")
plt.ylabel("Total Time(min)")

plt.legend(handles=[arrivingtime,startingtime,workingtime,finishtime,waitingtime],
           loc = 'upper left')

plt.show()

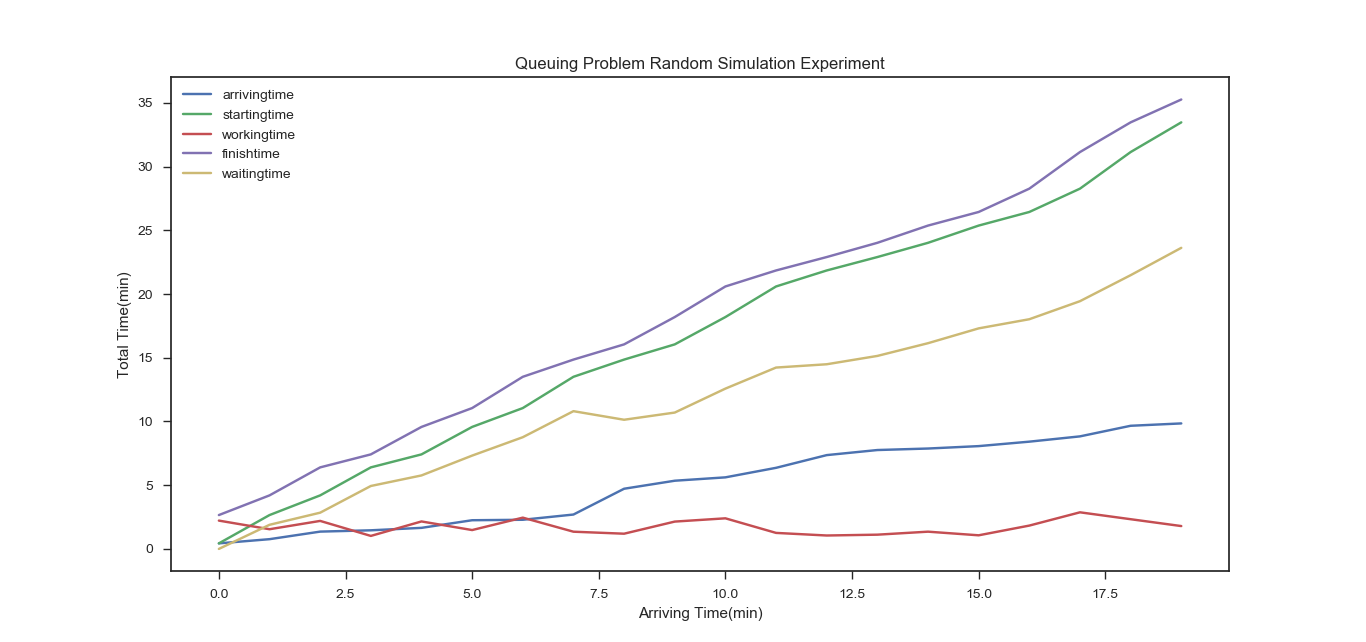
运行结果