桶排序/基数排序(Radix Sort)

说基数排序之前，我们先说桶排序：

基本思想：是将阵列分到有限数量的桶子里。每个桶子再个别排序（有可能再使用别的排序算法或是以递回方式继续使用桶排序进行排序）。桶排序是鸽巢排序的一种归纳结果。当要被排序的阵列内的数值是均匀分配的时候，桶排序使用线性时间（Θ（n））。但桶排序并不是 比较排序，他不受到 O(n log n) 下限的影响。
         简单来说，就是把数据分组，放在一个个的桶中，然后对每个桶里面的在进行排序。

例如要对大小为[1..1000]范围内的n个整数A[1..n]排序

首先，可以把桶设为大小为10的范围，具体而言，设集合B[1]存储[1..10]的整数，集合B[2]存储   (10..20]的整数，……集合B[i]存储(   (i-1)*10,   i*10]的整数，i   =   1,2,..100。总共有  100个桶。

然后，对A[1..n]从头到尾扫描一遍，把每个A[i]放入对应的桶B[j]中。  再对这100个桶中每个桶里的数字排序，这时可用冒泡，选择，乃至快排，一般来说任  何排序法都可以。

最后，依次输出每个桶里面的数字，且每个桶中的数字从小到大输出，这  样就得到所有数字排好序的一个序列了。

假设有n个数字，有m个桶，如果数字是平均分布的，则每个桶里面平均有n/m个数字。如果

对每个桶中的数字采用快速排序，那么整个算法的复杂度是

O(n   +   m   *   n/m*log(n/m))   =   O(n   +   nlogn   -   nlogm)

从上式看出，当m接近n的时候，桶排序复杂度接近O(n)

当然，以上复杂度的计算是基于输入的n个数字是平均分布这个假设的。这个假设是很强的  ，实际应用中效果并没有这么好。如果所有的数字都落在同一个桶中，那就退化成一般的排序了。

前面说的几大排序算法 ，大部分时间复杂度都是O（n2），也有部分排序算法时间复杂度是O(nlogn)。而桶式排序却能实现O（n）的时间复杂度。但桶排序的缺点是：

1）首先是空间复杂度比较高，需要的额外开销大。排序有两个数组的空间开销，一个存放待排序数组，一个就是所谓的桶，比如待排序值是从0到m-1，那就需要m个桶，这个桶数组就要至少m个空间。

2）其次待排序的元素都要在一定的范围内等等。

桶式排序是一种分配排序。分配排序的特定是不需要进行关键码的比较，但前提是要知道待排序列的一些具体情况。

 

分配排序的基本思想：实例:

扑克牌中52 张牌，可按花色和面值分成两个字段，其大小关系为：
花色： 梅花< 方块< 红心< 黑心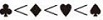  
面值： 2 < 3 < 4 < 5 < 6 < 7 < 8 < 9 < 10 < J < Q < K < A

若对扑克牌按花色、面值进行升序排序，得到如下序列：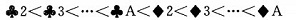

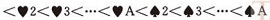
即两张牌，若花色不同，不论面值怎样，花色低的那张牌小于花色高的，只有在同花色情况下，大小关系才由面值的大小确定。这就是多关键码排序。

为得到排序结果，我们讨论两种排序方法。
方法1：先对花色排序，将其分为4 个组，即梅花组、方块组、红心组、黑心组。再对每个组分别按面值进行排序，最后，将4 个组连接起来即可。
方法2：先按13 个面值给出13 个编号组(2 号，3 号，...，A 号)，将牌按面值依次放入对应的编号组，分成13 堆。再按花色给出4 个编号组(梅花、方块、红心、黑心)，将2号组中牌取出分别放入对应花色组，再将3 号组中牌取出分别放入对应花色组，……，这样，4 个花色组中均按面值有序，然后，将4 个花色组依次连接起来即可。

设n 个元素的待排序列包含d 个关键码{k1，k2，…，kd}，则称序列对关键码{k1，k2，…，kd}有序是指：对于序列中任两个记录r[i]和r[j](1≤i≤j≤n)都满足下列有序关系：

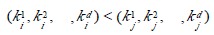
其中k1 称为最主位关键码，kd 称为最次位关键码     。

两种多关键码排序方法：

多关键码排序按照从最主位关键码到最次位关键码或从最次位到最主位关键码的顺序逐次排序，分两种方法：

最高位优先(Most Significant Digit first)法，简称MSD 法：

1）先按k1 排序分组，将序列分成若干子序列，同一组序列的记录中，关键码k1 相等。

2）再对各组按k2 排序分成子组，之后，对后面的关键码继续这样的排序分组，直到按最次位关键码kd 对各子组排序后。

3）再将各组连接起来，便得到一个有序序列。扑克牌按花色、面值排序中介绍的方法一即是MSD 法。

最低位优先(Least Significant Digit first)法，简称LSD 法：

1) 先从kd 开始排序，再对kd-1进行排序，依次重复，直到按k1排序分组分成最小的子序列后。

2) 最后将各个子序列连接起来，便可得到一个有序的序列, 扑克牌按花色、面值排序中介绍的方法二即是LSD 法。

基于LSD方法的链式基数排序的基本思想

　　“多关键字排序”的思想实现“单关键字排序”。对数字型或字符型的单关键字，可以看作由多个数位或多个字符构成的多关键字，此时可以采用“分配-收集”的方法进行排序，这一过程称作基数排序法，其中每个数字或字符可能的取值个数称为基数。比如，扑克牌的花色基数为4，面值基数为13。在整理扑克牌时，既可以先按花色整理，也可以先按面值整理。按花色整理时，先按红、黑、方、花的顺序分成4摞（分配），再按此顺序再叠放在一起（收集），然后按面值的顺序分成13摞（分配），再按此顺序叠放在一起（收集），如此进行二次分配和收集即可将扑克牌排列有序。

基数排序:

是按照低位先排序，然后收集；再按照高位排序，然后再收集；依次类推，直到最高位。有时候有些属性是有优先级顺序的，先按低优先级排序，再按高优先级排序。最后的次序就是高优先级高的在前，高优先级相同的低优先级高的在前。基数排序基于分别排序，分别收集，所以是稳定的。

算法实现：

Void RadixSort(Node L[],length,maxradix)
{
   int m,n,k,lsp;
   k=1;m=1;
   int temp[10][length-1];
   Empty(temp); //清空临时空间
   while(k<maxradix) //遍历所有关键字
   {
     for(int i=0;i<length;i++) //分配过程
    {
       if(L[i]<m)
          Temp[0][n]=L[i];
       else
          Lsp=(L[i]/m)%10; //确定关键字
       Temp[lsp][n]=L[i];
       n++;
   }
   CollectElement(L,Temp); //收集
   n=0;
   m=m*10;
  k++;
 }
}

总结

各种排序的稳定性，时间复杂度和空间复杂度总结：

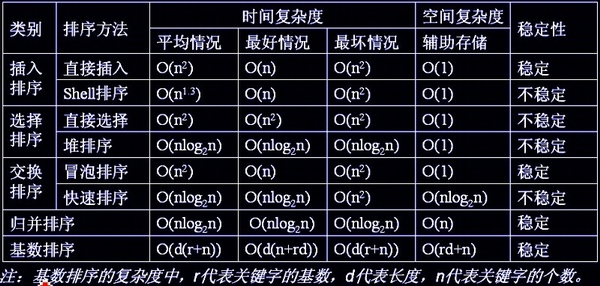
我们比较时间复杂度函数的情况：

时间复杂度函数O(n)的增长情况

所以对n较大的排序记录。一般的选择都是时间复杂度为O(nlog2n)的排序方法。

时间复杂度来说：

(1)平方阶(O(n²))排序
　　各类简单排序:直接插入、直接选择和冒泡排序；
 (2)线性对数阶(O(nlog2n))排序
　　快速排序、堆排序和归并排序；
 (3)O(n^1+§))排序,§是介于0和1之间的常数。

希尔排序
(4)线性阶(O(n))排序
　　基数排序，此外还有桶、箱排序。

说明：

当原表有序或基本有序时，直接插入排序和冒泡排序将大大减少比较次数和移动记录的次数，时间复杂度可降至O（n）；

而快速排序则相反，当原表基本有序时，将蜕化为冒泡排序，时间复杂度提高为O（n2）；

原表是否有序，对简单选择排序、堆排序、归并排序和基数排序的时间复杂度影响不大。

稳定性：

排序算法的稳定性:若待排序的序列中，存在多个具有相同关键字的记录，经过排序， 这些记录的相对次序保持不变，则称该算法是稳定的；若经排序后，记录的相对 次序发生了改变，则称该算法是不稳定的。 
     稳定性的好处：排序算法如果是稳定的，那么从一个键上排序，然后再从另一个键上排序，第一个键排序的结果可以为第二个键排序所用。基数排序就是这样，先按低位排序，逐次按高位排序，低位相同的元素其顺序再高位也相同时是不会改变的。另外，如果排序算法稳定，可以避免多余的比较；

稳定的排序算法：冒泡排序、插入排序、归并排序和基数排序

不是稳定的排序算法：选择排序、快速排序、希尔排序、堆排序

选择排序算法准则：

每种排序算法都各有优缺点。因此，在实用时需根据不同情况适当选用，甚至可以将多种方法结合起来使用。

选择排序算法的依据

影响排序的因素有很多，平均时间复杂度低的算法并不一定就是最优的。相反，有时平均时间复杂度高的算法可能更适合某些特殊情况。同时，选择算法时还得考虑它的可读性，以利于软件的维护。一般而言，需要考虑的因素有以下四点：

1．待排序的记录数目n的大小；

2．记录本身数据量的大小，也就是记录中除关键字外的其他信息量的大小；

3．关键字的结构及其分布情况；

4．对排序稳定性的要求。

设待排序元素的个数为n.

1）当n较大，则应采用时间复杂度为O(nlog2n)的排序方法：快速排序、堆排序或归并排序序。

快速排序：是目前基于比较的内部排序中被认为是最好的方法，当待排序的关键字是随机分布时，快速排序的平均时间最短；
       堆排序 ：  如果内存空间允许且要求稳定性的，

归并排序：它有一定数量的数据移动，所以我们可能过与插入排序组合，先获得一定长度的序列，然后再合并，在效率上将有所提高。

2）  当n较大，内存空间允许，且要求稳定性 =》归并排序

3）当n较小，可采用直接插入或直接选择排序。

直接插入排序：当元素分布有序，直接插入排序将大大减少比较次数和移动记录的次数。

直接选择排序 ：元素分布有序，如果不要求稳定性，选择直接选择排序

5）一般不使用或不直接使用传统的冒泡排序。

6）基数排序
它是一种稳定的排序算法，但有一定的局限性：
　　1、关键字可分解。
　　2、记录的关键字位数较少，如果密集更好
　　3、如果是数字时，最好是无符号的，否则将增加相应的映射复杂度，可先将其