[UVa 1326]Jurassic Remains

题解

在一个字符串中，每个字符出现的次数本身是无关紧要的，重要的只是这些次数的奇偶性，因此想到用一个二进制的位表示一个字母（$1$表示出现奇数次，$0$表示出现偶数次）。比如样例的$6$个数，写成二进制后如图所示。

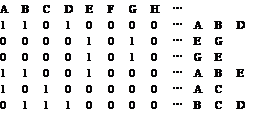
此时，问题转化为求尽量多的数，使得它们的$xor$值为$0$。

最容易想到的方法是直接穷举，时间复杂度为$O(2^n)$，有些偏大。注意到$xor$值为$0$的两个整数必须完全相等，我们可以把字符串分成两个部分：首先计算前$n \over 2$个字符串所能得到的所有$xor$值，并将其保存到一个映射$S$（$xor$值->前$n \over 2$个字符串的一个子集）中；然后枚举后$n \over 2$个字符串所能得到的所有$xor$值，并每次都在$S$中查找。

如果映射用$STL$的$map$实现，总时间复杂度为$O(2^{n \over 2}log_2 n)$，即$O(1.44^n log_2 n)$，比第一种方法好了很多。

 //It is made by Awson on 2017.9.20
 #include <set>
 #include <map>
 #include <cmath>
 #include <ctime>
 #include <queue>
 #include <stack>
 #include <string>
 #include <cstdio>
 #include <vector>
 #include <cstdlib>
 #include <cstring>
 #include <iostream>
 #include <algorithm>
 #define Min(a, b) ((a) < (b) ? (a) : (b))
 #define Max(a, b) ((a) > (b) ? (a) : (b))
 #define lowbit(x) ((x)&(-(x)))
 #define LL long long
 using namespace std;

 int n;
 char ch[];
 int a[];
 map<int, int> mp;

 int bitcount(int x) {
     int cnt = ;
     for (; x; x -= lowbit(x)) cnt++;
     return cnt;
 }

 void work() {
     for (int i = ; i < n; i++) {
         scanf("%s", ch);
         a[i] = ;
         for (int j = ; j < strlen(ch); j++) a[i] ^= <<ch[j]-'A';
     }
     mp.clear();
     int mid = n/;
     int lim = <<mid;
     for (int i = ; i < lim; i++) {
         int tmp = ;
         for (int j = ; j < mid; j++)
             if (i&(<<j)) tmp ^= a[j];
         if (!mp.count(tmp) || bitcount(mp[tmp]) < bitcount(i))
             mp[tmp] = i;
     }
     int ans = ;
     lim = <<(n-mid);
     for (int i = ; i < lim; i++) {
         int tmp = ;
         for (int j = mid; j < n; j++)
             if (i&(<<j-mid)) tmp ^= a[j];
         if (mp.count(tmp) && bitcount(ans) < bitcount(mp[tmp])+bitcount(i)) ans = (i<<mid)|mp[tmp];
     }
     printf("%d\n", bitcount(ans));
     for (int i = ; i < n; i++)
         if (ans&(<<i)) printf("%d ", i+);
     putchar('\n');
 }
 int main() {
     while (~scanf("%d", &n))
         work();
     return ;
 }