关于 f 散度

在概率统计中，f散度是一个函数，这个函数用来衡量两个概率密度p和q的区别，也就是衡量这两个分布多么的相同或者不同。

1.f散度的定义
p和q是同一个空间中的两个概率密度函数，它们之间的f散度可以用如下方程表示：

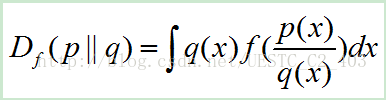
f函数满足两个条件：f函数是一个凸函数，并且f(1)=0。

2.f散度的特例
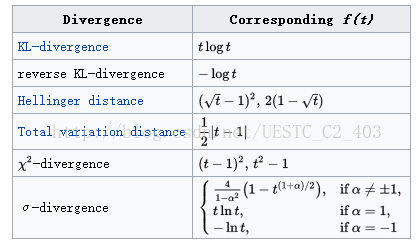
如果f(x)=xlogx，那就是KL散度。如果是f(x)=-logx，那就表示reverse KL散度。

3.f散度的非负性
因为f是凸函数，E(f(x))>=f(E(x))，所以

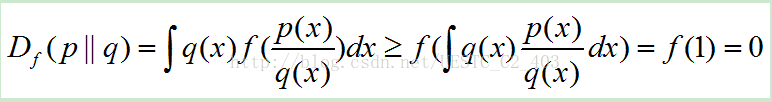
这就是为什么需要上面提到的满足的两个条件。

参考：https://en.wikipedia.org/wiki/F-divergence
---------------------

原文：https://blog.csdn.net/uestc_c2_403/article/details/75208644