HDU 2829 - Lawrence - [斜率DP]

题目链接：http://acm.hdu.edu.cn/showproblem.php?pid=2829

T. E. Lawrence was a controversial figure during World War I. He was a British officer who served in the Arabian theater and led a group of Arab nationals in guerilla strikes against the Ottoman Empire. His primary targets were the railroads. A highly fictionalized version of his exploits was presented in the blockbuster movie, "Lawrence of Arabia".

You are to write a program to help Lawrence figure out how to best use his limited resources. You have some information from British Intelligence. First, the rail line is completely linear---there are no branches, no spurs. Next, British Intelligence has assigned a Strategic Importance to each depot---an integer from 1 to 100. A depot is of no use on its own, it only has value if it is connected to other depots. The Strategic Value of the entire railroad is calculated by adding up the products of the Strategic Values for every pair of depots that are connected, directly or indirectly, by the rail line. Consider this railroad: 

Its Strategic Value is 4*5 + 4*1 + 4*2 + 5*1 + 5*2 + 1*2 = 49.

Now, suppose that Lawrence only has enough resources for one attack. He cannot attack the depots themselves---they are too well defended. He must attack the rail line between depots, in the middle of the desert. Consider what would happen if Lawrence attacked this rail line right in the middle: 

The Strategic Value of the remaining railroad is 4*5 + 1*2 = 22. But, suppose Lawrence attacks between the 4 and 5 depots: 

The Strategic Value of the remaining railroad is 5*1 + 5*2 + 1*2 = 17. This is Lawrence's best option.

Given a description of a railroad and the number of attacks that Lawrence can perform, figure out the smallest Strategic Value that he can achieve for that railroad.

Input

There will be several data sets. Each data set will begin with a line with two integers, n and m. n is the number of depots on the railroad (1≤n≤1000), and m is the number of attacks Lawrence has resources for (0≤m<n). On the next line will be n integers, each from 1 to 100, indicating the Strategic Value of each depot in order. End of input will be marked by a line with n=0 and m=0, which should not be processed.

Output

For each data set, output a single integer, indicating the smallest Strategic Value for the railroad that Lawrence can achieve with his attacks. Output each integer in its own line.

Sample Input

4 1
4 5 1 2
4 2
4 5 1 2
0 0

Sample Output

17
2

题意：

给出一条笔直无分叉的铁路上有n个仓库，每个仓库有一个v[i]代表价值；

每两个仓库之间算作一段铁路，现在有m次攻击机会，一次攻击可以炸毁一段铁路；

m次攻击后，剩余的总价值为：Σ(v[i]*v[j])，i和j为所有任意两个互相可到达的仓库。

现要求选定m段铁路进行攻击炸毁，然后使得总价值最小。

题解：

设dp[i][j]是前i个仓库，炸掉j段铁路后，剩余总价值的最小值。（显然，j<i）

设w[a][b]表示铁路完好的情况下，从a仓库到b仓库的总价值，即：

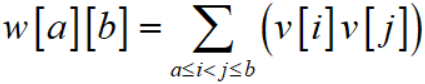
那么，就有：

dp[i][j] = min( dp[k][j-1] + w[k+1][i] )，j≤k<i；

方程的意义是：炸毁仓库k和仓库k+1之间的那段铁路（即第k段铁路），算出总价值，枚举k找到最小的。

那么如何计算w[k+1][i]呢？

假设$sum\left[ i \right] = \sum\limits_{k = 1}^i {v\left[ k \right]}$，那么就有：

w[1][i] = w[1][k] + w[k+1][i] + (v[1]+v[2]+…+v[k]) × (v[k+1]+v[k+2]+…+v[i])

　　　= w[1][k] + w[k+1][i] + sum[k] × (sum[i]-sum[k])

即w[k+1][i] = w[1][i] - w[1][k] - sum[k] × (sum[i]-sum[k])

我们把w[k+1][i]的计算式带入状态转移方程得到：

dp[i][j] = min{ dp[k][j-1] + w[1][i] - w[1][k] - sum[k] × (sum[i]-sum[k]) }

那么，对于这个DP，j一个循环、i一个循环、k一个循环，就是O(n³)的时间复杂度；

需要斜率优化，优化到O(n²)即可。

对于第a段铁路和第b段铁路（1≤a<b<i），我们若有：

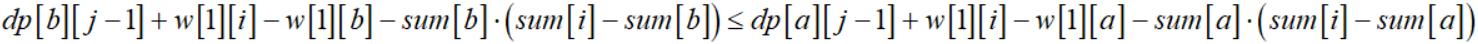
可以说第b段铁路优于第a段铁路。

对上式进行变形可得：

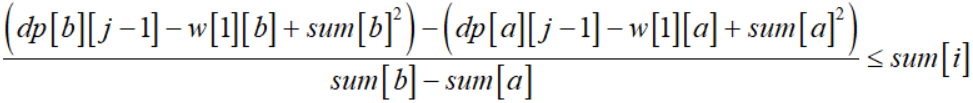
我们假设：

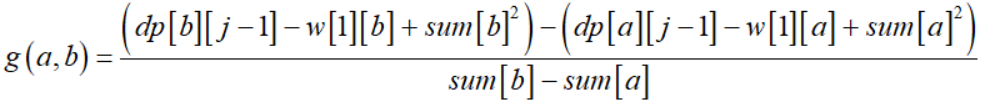
那么

选择炸毁第b段铁路优于炸毁第a段铁路　<=>　g(a,b) ≤ sum[i]

选择炸毁第b段铁路劣于炸毁第a段铁路　<=>　g(a,b) > sum[i]

然后后面的操作就和HDU3507http://www.cnblogs.com/dilthey/p/8745843.html差不多了：

①在计算dp[i][j]时，若有j≤a<b<c<i，只要满足g(a,b) ≥ g(b,c)，则b点必然被淘汰.

证明：若g(b,c) ≤ sum[i]，则选择第c段铁路优于第b段铁路，b淘汰；

　　　若g(b,c) > sum[i]，则g(a,b) > sum[i]，则选第b段铁路差于第a段，b淘汰。

②若在计算dp[i][j]时，k点被淘汰，则计算dp[i+1][j]时，k点必然也被淘汰.

AC代码：

#include<bits/stdc++.h>
using namespace std;
const int maxn=1e3+;

int n,m;
int sum[maxn]; //前缀和
int w[maxn]; //w[1][i]
int dp[maxn][maxn];
int q[maxn],head,tail;

double g(int a,int b,int j)
{
    double up = (dp[b][j-]-w[b]+sum[b]*sum[b]) - (dp[a][j-]-w[a]+sum[a]*sum[a]);
    double down = sum[b]-sum[a];
    return up/down;
}
int main()
{
    while(scanf("%d%d",&n,&m) && n+m>)
    {
        sum[]=;
        for(int i=,tmp;i<=n;i++)
        {
            scanf("%d",&tmp);
            sum[i]=sum[i-]+tmp;
            w[i]=w[i-]+sum[i-]*tmp;
        }

        for(int i=;i<=n;i++) dp[i][]=w[i];
        for(int j=;j<=m;j++)
        {
            head=tail=;
            q[tail++]=j;
            for(int i=j+,a,b;i<=n;i++)
            {
                while(head+<tail)
                {
                    a=q[head], b=q[head+];
                    if(g(a,b,j)<=sum[i]) head++;
                    else break;
                }
                int k=q[head];
                dp[i][j]=dp[k][j-]+w[i]-w[k]-sum[k]*(sum[i]-sum[k]);

                while(head+<tail)
                {
                    a=q[tail-], b=q[tail-];
                    if(g(a,b,j)>=g(b,i,j)) tail--;
                    else break;
                }
                q[tail++]=i;
            }
        }

        printf("%d\n",dp[n][m]);
    }
}

注意点：

本题看到v[i]在1到100之间，所以不会出现sum[b]-sum[a]=0这种除数为零的情况，所以可以直接求g(a,b)，而不用再转成乘法比大小。

斜率DP也算是有一定的套路，能够优化一维的时间复杂度，所以刚开始做斜率DP的时候，应先从普通的DP进行考虑（包括条件初始化、状态转移的顺序之类），然后再考虑加入斜率优化。