PCL点云特征描述与提取（2）

点特征直方图（PFH）描述子

正如点特征表示法所示，表面法线和曲率估计是某个点周围的几何特征基本表示法。虽然计算非常快速容易，但是无法获得太多信息，因为它们只使用很少的几个参数值来近似表示一个点的k邻域的几何特征。然而大部分场景中包含许多特征点，这些特征点有相同的或者非常相近的特征值，因此采用点特征表示法，其直接结果就减少了全局的特征信息。那么三维特征描述子中一位成员：点特征直方图(Point Feature Histograms)，我们简称为PFH，从PCL实现的角度讨论其实施细节。PFH特征不仅与坐标轴三维数据有关，同时还与表面法线有关。

PFH计算方式通过参数化查询点与邻域点之间的空间差异，并形成一个多维直方图对点的k邻域几何属性进行描述。直方图所在的高维超空间为特征表示提供了一个可度量的信息空间，对点云对应曲面的6维姿态来说它具有不变性，并且在不同的采样密度或邻域的噪音等级下具有鲁棒性。点特征直方图（PFH）表示法是基于点与其k邻域之间的关系以及它们的估计法线，简言之，它考虑估计法线方向之间所有的相互作用，试图捕获最好的样本表面变化情况，以描述样本的几何特征。因此，合成特征超空间取决于每个点的表面法线估计的质量。如图所示，表示的是一个查询点(Pq) 的PFH计算的影响区域，Pq 用红色标注并放在圆球的中间位置，半径为r， (Pq)的所有k邻元素（即与点Pq的距离小于半径r的所有点）全部互相连接在一个网络中。最终的PFH描述子通过计算邻域内所有两点之间关系而得到的直方图，因此存在一个O(k) 的计算复杂性。

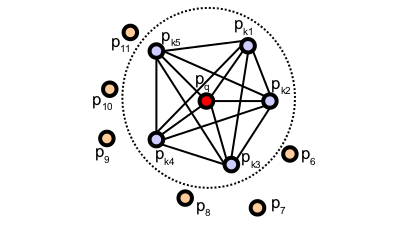
查询点 的PFH计算的影响区域

为了计算两点Pi和Pj及与它们对应的法线Ni和Nj之间的相对偏差，在其中的一个点上定义一个固定的局部坐标系，如图2所示。

                                         

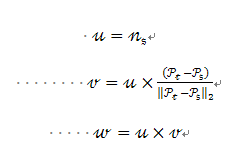
使用上图中uvw坐标系，法线 和 之间的偏差可以用一组角度来表示，如下所示：

d是两点Ps和Pt之间的欧氏距离, 。计算k邻域内的每一对点的四组值，这样就把两点和它们法线相关的12个参数（xyz坐标值和法线信息）减少到4个

为查询点创建最终的PFH表示，所有的四元组将会以某种统计的方式放进直方图中，这个过程首先把每个特征值范围划分为b个子区间，并统计落在每个子区间的点数目，因为四分之三的特征在上述中为法线之间的角度计量，在三角化圆上可以将它们的参数值非常容易地归一到相同的区间内。一个统计的例子是：把每个特征区间划分成等分的相同数目，为此在一个完全关联的空间内创建有 个区间的直方图。在这个空间中，一个直方图中某一区间统计个数的增一对应一个点的四个特征值。如图3所示，就是点云中不同点的点特征直方图表示法的一个例子，在某些情况下，第四个特征量d在通常由机器人捕获的2.5维数据集中的并不重要，因为临近点间的距离从视点开始是递增的，而并非不变的，在扫描中局部点密度影响特征时，实践证明省略d是有益的。

更详细的解释：pointclouds.org/documentation/tutorials/how_features_work.php#rusudissertation

估计PFH特征

点特征直方图（PFH）在PCL中的实现是pcl_features模块的一部分。默认PFH的实现使用5个区间分类（例如：四个特征值中的每个都使用5个区间来统计），

以下代码段将对输入数据集中的所有点估计其对应的PFH特征。

 #include <pcl/point_types.h>                  //点类型头文件

#include <pcl/features/pfh.h>                 //pfh特征估计类头文件

...//其他相关操作

pcl::PointCloud<pcl::PointXYZ>::Ptrcloud(new pcl::PointCloud<pcl::PointXYZ>);

pcl::PointCloud<pcl::Normal>::Ptrnormals(new pcl::PointCloud<pcl::Normal>());

...//打开点云文件估计法线等

//创建PFH估计对象pfh，并将输入点云数据集cloud和法线normals传递给它

pcl::PFHEstimation<pcl::PointXYZ,pcl::Normal,pcl::PFHSignature125> pfh;

pfh.setInputCloud(cloud);

pfh.setInputNormals(normals);

//如果点云是类型为PointNormal,则执行pfh.setInputNormals (cloud);

//创建一个空的kd树表示法，并把它传递给PFH估计对象。

//基于已给的输入数据集，建立kdtree

pcl::KdTreeFLANN<pcl::PointXYZ>::Ptrtree(new pcl::KdTreeFLANN<pcl::PointXYZ>());

pfh.setSearchMethod(tree);

//输出数据集

pcl::PointCloud<pcl::PFHSignature125>::Ptrpfhs(new pcl::PointCloud<pcl::PFHSignature125>());

//使用半径在5厘米范围内的所有邻元素。

//注意：此处使用的半径必须要大于估计表面法线时使用的半径!!!

pfh.setRadiusSearch(0.05);

//计算pfh特征值

pfh.compute(*pfhs);

// pfhs->points.size ()应该与input cloud->points.size ()有相同的大小，即每个点都有一个pfh特征向量

PFHEstimation类的实际计算程序内部只执行以下：

对点云P中的每个点p

1.得到p点的最近邻元素

2.对于邻域内的每对点，计算其三个角度特征参数值

3.将所有结果统计到一个输出直方图中

微信公众号号可扫描二维码一起共同学习交流