Andrew Ng-ML-第十三章-支持向量机

1.从代价函数谈起SVM

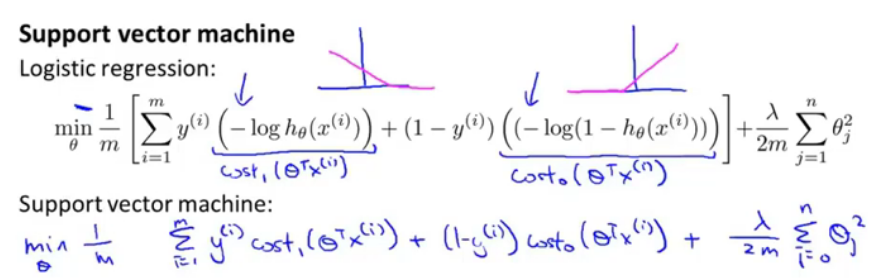
图一

根据将y=0||y=1，得到逻辑回归的代价函数，那么SVM和其代价函数是相似的，只不过是引入了cost0与cost1,并且自变量使用了theta_T*x(i)，并且由于SVM的通常表示方法，得到了如下的优化函数假设：

在代价函数项加上了系数C(=1/lamda)，也就是C很小时，后边一项的权重较大，SVM的模型，如果theta_T*x>=0，那么模型输出1，否则输出0.

SVM就是将负样本和正样本以最大间距分开。

优化目标如上，当要最小化时，C若设置为非常大时，那么要让第一项为0，当一个样本是yi=1时，就需要θTxi>=1，这个是跟据类斯ReLU函数来决定的；

当一个样本是yi=0时，那么第一项中只有后半部分在，就要求θTxi<=-1这一项就为0了；

那么当第一项为0之后，就是最小化第二项的问题了。min后一项，并且限制条件是右下角（只有满足条件才可以保证前一项为0啊！）

2.SVM为何能选取最大间隔的平面？

图二

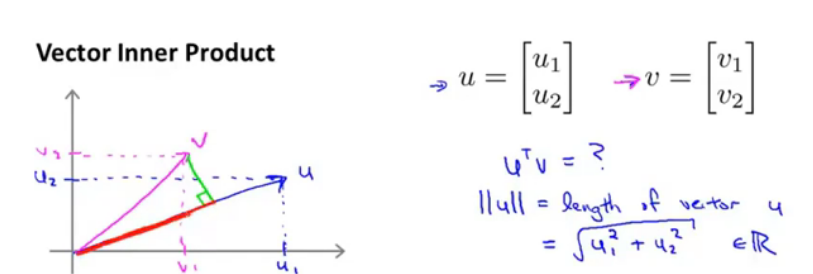
向量的内积，对单个向量来说，它的第二范数也就相当于是向量的长度（从原点出发），而内积相当于v在u上的投影长度（有正有负）*u的长度。

图三

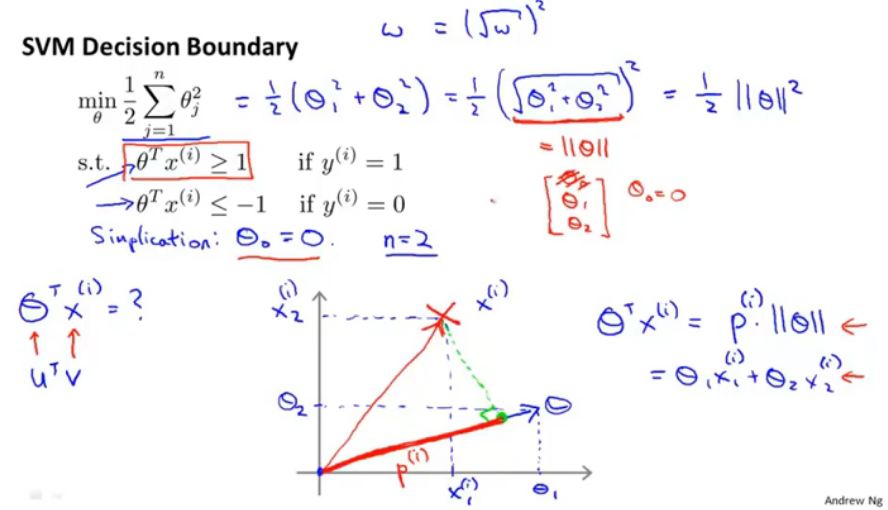
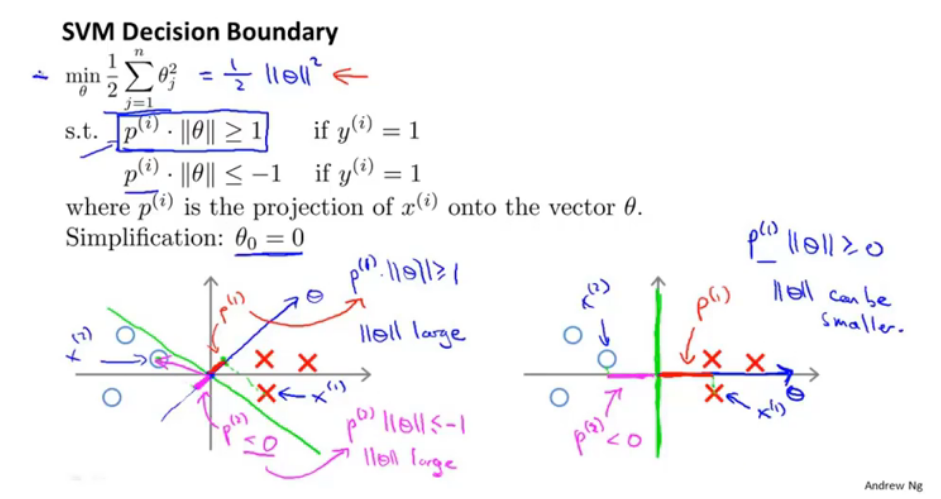
当只有两个特征时，theta1和theta2即相当于theta向量的范数的平方，而通过公式（右下角）将优化条件限制为正样本点在分割平面的正侧法线（theta向量方向）的投影长度*theta向量的长度，所以就min||theta||的同时需要保证条件≥1，就需要正样本点在theta方向上的投影值最大。如下图：

图四

//PS不太明白，为什么theta向量是和超平面垂直的？保留问题。

3.高斯核函数原理介绍

图五

给出三个标志点，对任一数据点x,都计算，计算x和三个给定点的相似度，计算相似度的公式图中给出的是高斯核函数，即x与每个点的距离的平方/-2*6^2，这个相似度函数就是核函数。又给出了一个十分传神的例子：

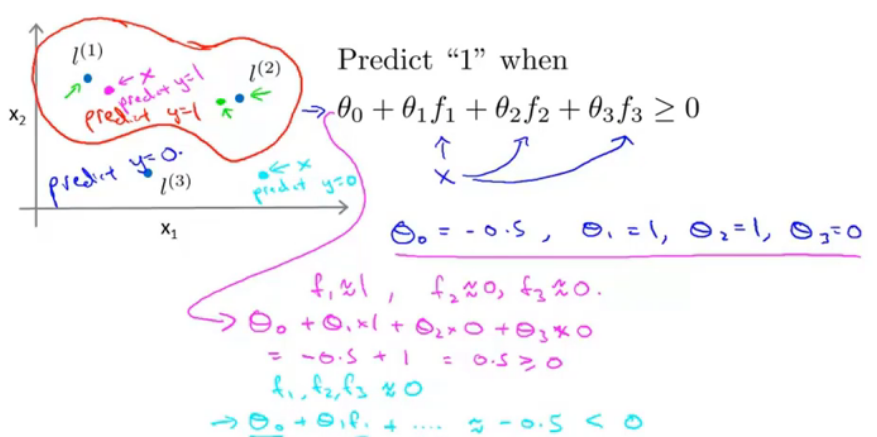
图六

当？≥0时，预测类为正类，那么取theta为以下，根据高斯和函数的性质，如果点x和l距离很近，那么≈1；距离很远，那么结果≈0。通过这样就可以得出一个分界面。这是一个我从前没有了解过的角度！下一节就讲到该如何选取这些landmark。

4.高斯核函数中landmark的选取

图七

这里的landmark选取是通过将训练集中的每个点都作为landmark,共m个，给定一个点，那么就会计算与其他所有点的相似度，其中会有一个是与自身的相似度，那么就=1，这样通过相似度函数，也就是核函数，可以将原本的x(i)映射到一个m+1维的f向量中，并且让f去参与运算，f就是用于描述训练样本的特征向量。

图八

在8中，使用f去计算，并且损失函数中代入f去计算，所以最终优化项中求和是从1求到m,或者说n=m.//不太明白这里相等是什么意思。通常theta^2求和都被写为thetaTtheta. 还有中间加上M的，不太明白是什么意思。

大多数SVM实现的时候，是将thetaTtheta替换为中间*M（M取决于使用的核函数），这是另一种区别于求||theta||^2的距离求解方式。这种方式让SVM运行更加高效，适用于有更大的训练集。主要是为了运算效率。

5.SVM参数中偏差-方差的问题

图九

C也就相当于逻辑回归正则化项系数的倒数，当C很大时，即lamd较小，也就是忽略正则化项，偏差较小，方差较大，（是说系数向量吗？）；当C很小时，即lamd较大，即计算正则化项，那么偏差较大（即欠拟合状态）方差较小。而对应高斯核函数中的参数6^2,当其较大时，函数趋于平滑，偏差较大，方差较小；当其较小时，偏差较小，方差较大。//不太明白是什么意思。

6.SVM中的核函数适用情况

图十

使用SVM软件包来找出参数theta，需要指明参数C和使用的核函数：

没有核函数（即线性核函数）：适用于当n很大，m很小，即特征很多，但是样本量少的情况。

高斯核函数：还需要指明参数6^2,当n较小，m很大时，即特征较少，样本量大的情况。这两个核函数是最常见的，也是使用最频繁的。

在使用核函数时还需要注意的问题，就是归一化，如下图：

 图十一

在使用核函数计算特征向量时，需要对输入向量进行归一化，如当一个特征是房价，另一个是卧室数量，那么v的大小就只受房价控制了。

7.其他的核函数

图十二

多项式核函数，有12中的几种形式，使用它时需要指明常数与幂次。还有更多的，字符串核函数（在做文本分类时，需要计算不同的字符串之间的距离）

8.使用逻辑回归orSVM

图十三

1.当特征数较大时(n>=m,n=10,000,m=10-1000)，这时候使用逻辑回归或者没有核函数的SVM，（因为若使用复杂的核函数训练复杂的分类函数，可能会出现过拟合的情况）

2.当n较小时，m是中等的（n=1-1000,m=10-10,000），此时使用高斯核函数的SVM最优。

3.当n较小,m较大时，增加更多的特征，然后使用逻辑回归和没有核函数的SVM。

神经网络能够很好的解决所有的问题，但是训练时间会稍长一点。