Andrew Ng-ML-第十二章-机器学习系统设计

1.确定执行的优先级

图1.邮件垃圾分类举例

选择100个单词作为指示是否是垃圾邮件的指标，将这些单词作为特征向量，只用0/1表示，出现多次也只用1表示，特征变量用来表示邮件。

通常情况下，会选择训练集中出现频率最多的n(在10000到50000)之间的几个单词。

图2.改进模型的建议

1.收集更多的数据。比如说honeypot就故意将邮箱地址暴露给垃圾邮件发送者，从而获取很多垃圾邮件作为数据集。

2.根据邮件路由信息（邮件头）。但是通常发送者会隐藏一些特征导致不能从邮件头中获取信息。

3.关注邮件体，比如单词的单复数discount和discounts应该被认为是一个单词吗？这单词变形之类的问题

4.创建一个复杂的算法来检测拼写错误，比如m0rtgage和w4tch.

2.误差分析（如何开始建立一个机器学习系统的步骤）

图3.建议的方法

第一步：首先是先建立一个简单的算法模型，然后在验证集上测试。（Ng会先花24小时做一个简单的速成模型，虽然效果并不好，但是具有指导意义）

第二步：画出学习曲线，以此来判断是增加更多数据，特征，或者是其他，这是很有帮助的。

第三步：误差分析。将误分类的数据，寻找这些误分类数据存在的特点。

做一个简单的学习模型可以指导接下来往哪个方面改进。

图4.误差分析

假如入当前是一个邮件垃圾检测，在误差分析时，假设有100个分类错误的（将垃圾邮件检测为正常，或将正常检测为错误），并人工检测这些邮件的特点：

(1)邮件的类型  （2）使算法能够正确分类的特征有哪些？

比如，卖药、卖赝品、窃取密码、等类型。特征包括：错误拼写(m0rgage和med1cine)、异常的邮件路由、异常的标点符号。

将精力放在简单模型误分类的邮件上，观察它们有什么特点。

图5.数值评估的重要性

对于邮件垃圾检测来说，是否需要使用词干提取算法，方法就是对比应用词干提取算法和不应用词干提取算法的情况下，给出一个具体的数值来衡量两者的优劣，即设定误差度量值，如在交叉验证集上的错误率，以此来评判模型是更好了，还是变差了。

总体本小节重点是：算法评估和误差度量值选择

另外，Ng强调，应该在验证集上做误差分析，而不是测试集上，在测试机上做误差分析是不符合数学原理的。

3.不对称性分类的误差评估

图6.偏斜类的分类例子

在癌症分类的例子中，训练了一个逻辑回归模型，当y=0时未患癌症，y=1时患癌症；模型在测试集上的误差是1%（99%诊断为正确）。

但是当前的数据集中，只有0.50%的癌症患者，那么这么来看1%的误差就很大了。

这样的数据集分布十分不均衡，一种远远大于另一种的情况就是偏斜集。

这时候如果我们直接使用图中的函数，直接将所有的分类y都设置为0，那么误差是0.5%(准确率为99.5%)，如果只从选取的误差度量值来看模型效果好了，但是模型的真正性能是否改进了？并没有。综上，对偏斜集不能使用误差度量值来表示模型是否改进了。

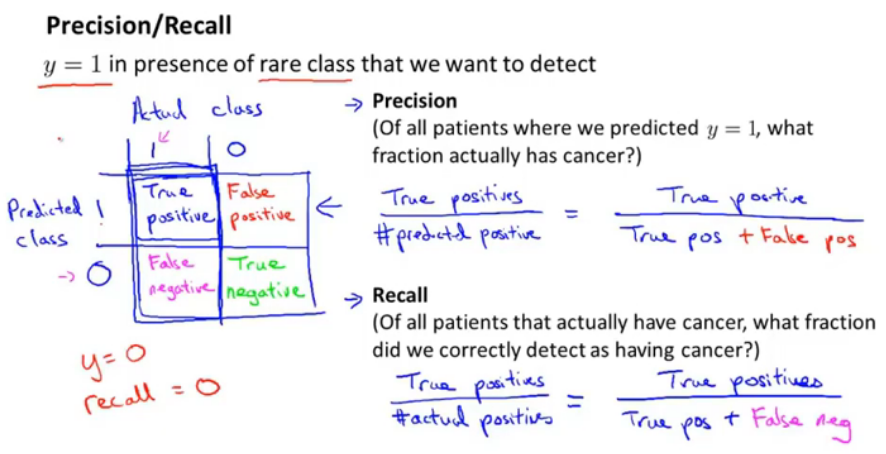
图7.查准率与召回（查全）率

当y=1出现很少时，需要检测查查准率吧和召回率。

方格中横轴是真正的类别：

查准率=真正类/预测为正类的=真正类/（假正类+真正类）——在预测为癌症的患者中，有多少是真正患癌症的？；

召回率=真正类/所有正的=真正类/（真正类+假负类）——在所有真正患癌症的患者中，有多少是被检测出来的?。

（如果使用y=0的话，召回率很低，在所有真正患癌症的人中，没有一个是被检测出来的）

对于偏斜类来说，如果这两个指标都非常高，那么就是一个好的学习算法。

4.查准率与召回率的权衡

图8.查准率与召回率的关系

在肿瘤预测的时候，可能不仅仅让h_θ(x)>=0.5而是让其>=0.9时，也就是说不轻易将病人判断为癌症患者。这就是一个阈值，是要70%的置信度还是90%的置信度来预测y=1。

假设只有在十分确信的情况下才将其判定为癌症患者，那么就是会 高查准率和低查全率；

假设不想误判为没有癌症，避免假正，就是高召回率和低查全率。

更加一般地，设置一个阈值根据其曲线，可以选择一个二者均衡的值，来判断y=1。然而是否有办法确定阈值的选择呢？看下边：

图9.好的回归模型

因为查准率与召回率是负关系，那么如何进行判断哪个模型更好呢？图中给出了两种判断方法，一种是平均值，但显然不行，算法3和算法1，算法3明显是不好的算法；

使用F1公式，来进行判断，当P、R均为0时，F1为0，P、R均为1时，F1为1，也就是整个的打分是在(0,1)之间的。这是一个好的权衡查准率与召回率的公式。

5.机器学习数据

图10.好的算法与大量数据

一个非常著名的结论表示，一个好的算法，好一个劣质的算法，但是对劣质算法给予了更多的数据，反而劣质算法表现得更好，因此有一个结论“谁能胜利，取决于谁有更多的数据而不是更好的算法”。

图11.大数据理论

当给出特征时，对人来说，能够根据预测出y呢？

当使用一个有很多参数的学习算法时（比如多特征的逻辑和线性回归，有很多隐含层的神经网络模型）那么假设它的一个低偏差的，即其训练误差很小；那么如果使用一个大的训练集，这样是不太可能去过拟合的，那么在测试集上的误差也就≈训练集上的误差；总的也就相当于测试误差也很小，那么这将是一个很好的回归模型。