Quasi-Newton Method--LBFGS

Quasi-Newton Method
Quasi-Newton Method每一步计算过程中仅涉及到函数值和函数梯度值计算，这样有效避免了Newton Method中涉及到的Hessian矩阵计算问题。于Newton Method不同的是Quasi-Newton Method在每点处构建一个如下的近似模型：

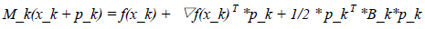
从上面的近似模型我们可以看出，该模型用B_k代替了Newton Method中近似模型中涉及到的Hessian矩阵。因此Quasi-Newton Method中方向计算公式如下所示：
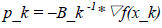(24)
这里有必要解释一下用于近似Hessian矩阵的B_k可行性，及一个指导性方案。根据Taylor(泰勒)级数可知如下公式：

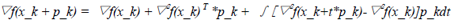
由于函数▽f(.)连续，因此上式可以表示为：

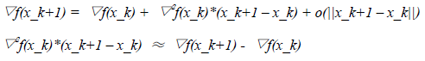
(25)
因此每一选择Hessian矩阵的近似B_ k+1时，可以像式(24)那样模仿真实的Hessian矩阵的性质。得到下式：
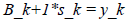(26)
其中：

s_k = x_k+1 – x_k y_k = ▽f(x_k+1) – ▽f(x_k) (27)

同时要求B_k+1为对称正定矩阵。

BFGS Method

从Quasi-Newton Method方向公式 (24) 中，可以看到每一步计算方向的过程中均涉及到B_k+1矩阵求逆的问题，为了避免该计算，通过分析公式（26）可知，我们可以构建一个近似H_k+1，该近视满足如下方程：

H_k+1*y_k = s_k (28)

同时要求H_k+1为对称正定矩阵。因此BFGS Method中，每个点处的方向由如下公式计算：

p_k = –H_k*▽f(x_k) (29)

在此基础上，BFGS方向迭代公式如下所示：

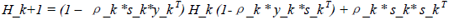
(30)
其中ρ_k为一个标量：

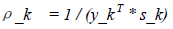
有了上面(30)的H_k迭代公式后，还有一个问题就是初始的H_0如何计算，目前常用的方法是初始的H_0直接设为单位矩阵I。因此BFGS Method用于解无约束最优化的过程可以表示为如下过程：

LBFGS Method
上一节所介绍的BFGS Method比较适合解决中小规模无约束最优化问题，但是BFGS算法产生的Hessian近似矩阵H_k为n * n的，同时该矩阵非稀疏，因此当n的规模较大时将面临两个问题：
1） 存储问题：n规模较大时，n*n矩阵对内存的消耗将较大；
2） 计算问题：n规模较大，同时n*n矩阵非稀疏时，计算复杂度将较高；
为了解决以上问题，引申出了Limited-Memory Quasi-Newton Method，目前使用较多的LBFGS算法即属于该类算法。为了减少H_k矩阵的存储，LBFGS算法利用最近几代的curvature 信息来构建Hessian矩阵的近似。由BFGS Method我们知道：

x_k+1 = x_k + a_k * H_k*▽f(x_k)

其中a_k为步长，H_k为Hessian矩阵的近似，可以通过如下迭代公式计算：

H_k+1 = V_k* H_k*V_k+ρ_k * s_k* s_k (31)

其中：

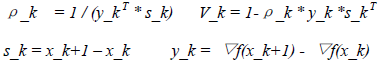
从上面的H_k的迭代计算公式可知，H_k会慢慢由稀疏矩阵转变为稠密矩阵，因此存储该矩阵以及进行该矩阵和向量的相乘运算的消耗将较大。为了避免该问题，LBFGS算法在BFGS算法的基础上从两点进行了改进：
1）估算每一步对应的Hessian近似矩阵时，给出一个当前步的初始Hessian矩阵估计H_k0
2) 利用过去当前代及过去m-1代的curvature信息修正初始Hessian矩阵估计H_k0，得到最终的Hessian矩阵近似估计H_k。
计算式如下所示：

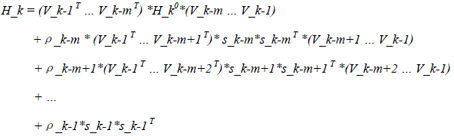
(32)
上述计算式(32），可以通过公式(31)递归计算获取。公式(32)可以用以下算法表示：

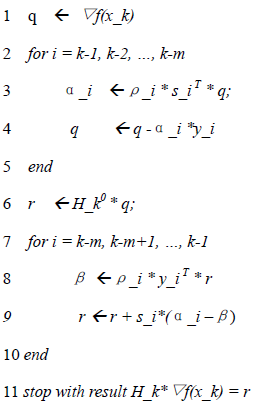
从上面计算H_k的公式(32)可知，要估算每个点x_k处的Hessian矩阵近似，需要给出初始估计H_k0，H_k0一般通过以下公式计算：

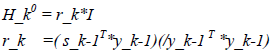
有了上面的方向计算算法后，LBFGS算法用于解无约束最优化问题，可以表示为如下算法：

1 选择一个初始点x_0，并选择收敛判断条件 ε> 0，以及常量m(代表过去代数)一般为6
2 k left 0 H_0 left I，因此r = H_0 *▽f(x_0) =▽f(x_0)
3 while ||▽f(x_k)|| > ε
4 计算从当前点x_k走到下一个点x_k+1的方向
p_k = –r
5 采用line search策略计算步长a_k
6 x_k+1 = x_k + a_k * p_k
7 if k > m
删除LBFGS计算H_k时用不上的向量对(s_k-m, y_k-m)
8 计算并保存 s_k = x_k+1 – x_k y_k = ▽f(x_k+1) – ▽f(x_k)
9 采用LBFGS Hessian矩阵近似算法计算 r
10 k left k+1

4．算法总结
用于解无约束优化算法的Quasi-Newton Method中的LBFGS算法到这里总算初步介绍完了，不过这里笔者要承认的是这篇文档省略了许多内容，包括算法收敛性的证明以及收敛速度证明等许多内容。因此读者若希望对这一块有一个更深入的认识可以参考以下两本书：
1) Numerical Methods for Unconstrained Optimization and Nonlinear Equations（J.E. Dennis Jr. Robert B. Schnabel）
2) Numerical Optimization（Jorge Nocedal Stephen J. Wright）