Codeforces886(Technocup2018) F Symmetric Projections

Codeforces886(Technocup2018) F Symmetric Projections

You are given a set of n points on the plane. A line containing the origin is called good, if projection of the given set to this line forms a symmetric multiset of points. Find the total number of good lines.

Multiset is a set where equal elements are allowed.

Multiset is called symmetric, if there is a point P on the plane such that the multiset is centrally symmetric in respect of point P.

Input

The first line contains a single integer \(n (1 ≤ n ≤ 2000)\) — the number of points in the set.

Each of the next n lines contains two integers \(x_i\) and \(y_i\) \(( - 10^6  ≤  x_i,  y_i  ≤  10^6)\) — the coordinates of the points. It is guaranteed that no two points coincide.

Output

If there are infinitely many good lines, print -1.

Otherwise, print single integer — the number of good lines.

Examples

input

3
1 2
2 1
3 3

output

3

input

2
4 3
1 2

output

-1

Note

Picture to the first sample test:

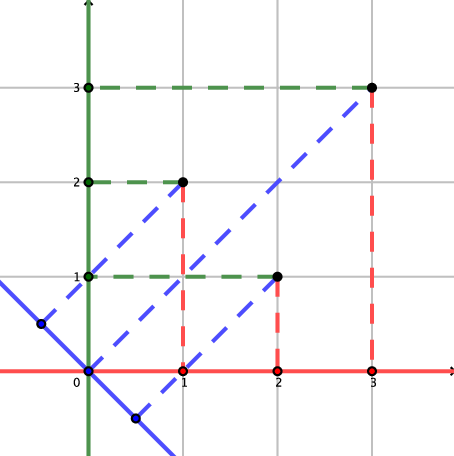
In the second sample, any line containing the origin is good.

题意描述

在平面上给出2000个点,求有多少条过原点的直线, 使这些点在直线上的投影对称

.

.

.

.

.

.

.

.

.

.

.

.

.

.

.

.

.

.

.

题解

(因为精度问题没过)

质心是所有点的平均坐标

???质心在合法的直线上的投影是对称重心???

假设两点是对称的, 那么他们的中点的投影必然是对称中心, 结合质心的性质, 这样可以唯一确定一条过原点的直线

注意到任意一点一定有投影后对称的点, 可能是自己, 所以只要随便拿一个点和\(n\)个点枚举就可以得到所有的可能直线, 即\(O(n)\)

判断直线可不可行有很多方式

需要基准点的题目可以把所有坐标改成相对坐标, 简化计算