力扣647(java)-回文子串（中等）

题目：

给你一个字符串 s ，请你统计并返回这个字符串中 回文子串 的数目。

回文字符串 是正着读和倒过来读一样的字符串。

子字符串 是字符串中的由连续字符组成的一个序列。

具有不同开始位置或结束位置的子串，即使是由相同的字符组成，也会被视作不同的子串。

示例 1：

输入：s = "abc"
输出：3
解释：三个回文子串: "a", "b", "c"
示例 2：

输入：s = "aaa"
输出：6
解释：6个回文子串: "a", "a", "a", "aa", "aa", "aaa"

提示：

1 <= s.length <= 1000
s 由小写英文字母组成

来源：力扣（LeetCode）
链接：https://leetcode.cn/problems/palindromic-substrings
著作权归领扣网络所有。商业转载请联系官方授权，非商业转载请注明出处。

解题思路：

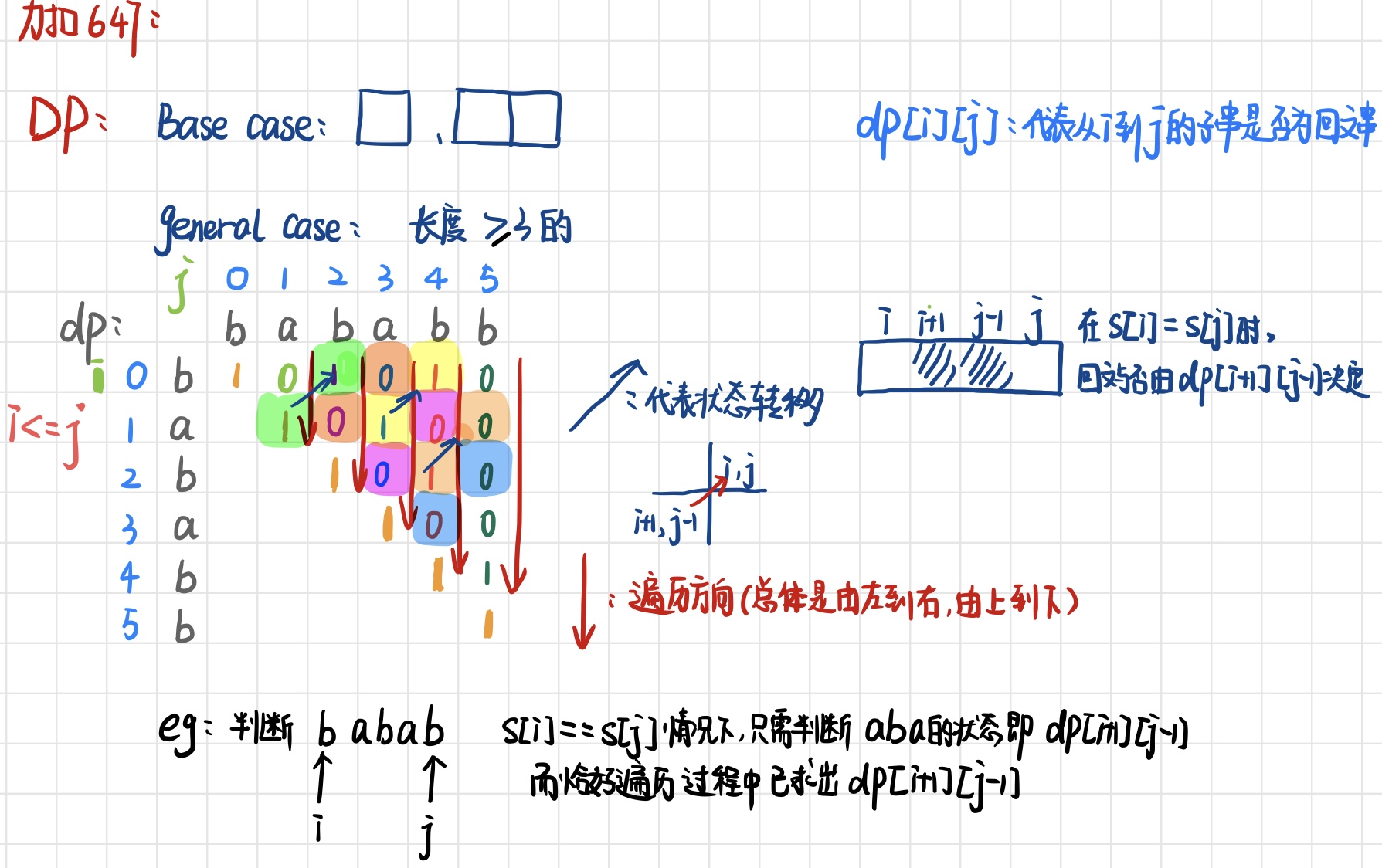
DP动态规划：

dp[i][j] :代表s中从i到j的子串是否为回文串。(boolean类型默认初始化就为false)

1.当s[i] != s[j],直接返回fasle;

2.当s[i] == s[j]时：

base case:

• 当只有一个字符时，肯定为回文字符串，例如 “ a ”；
• 当只有两个字符时，如果两个字符串相同，也是回文字符串，例如 “aa”；

这里 i 和 j 的关系： j - i < 2（ [ i, i ] , [ i, i+1 ] ）

general case:

• 当字符串有三个及以上的字符时，需要同时判断s[i] == s[j] 和 dp[i+1][j-1]成立。

故状态转移方程为：s[i] == s[j] && (j - i < 2 || dp[i+1][j-1]]) 时为回文串返回true，否则不是回文串，返回false。

遍历顺序：

i <= j ,由于dp[i][j] 的状态与dp[i+1][j-1]有关系，需要先算出dp[i+1][j-1], 所以遍历顺序应该为：从左上角开始，从上到下，从左到右。

代码：

 1 class Solution {
 2     public int countSubstrings(String s) {
 3         //由于提示中说了长度范围故没有为空情况
 4         int n = s.length();
 5         boolean[][] dp = new boolean[n][n];
 6         //统计回文子串的数
 7         int count = 0;
 8         for(int j = 0; j < n; j++){
 9             for(int i = 0; i <= j; i++){
10                 if(s.charAt(i) == s.charAt(j) && (j - i < 2 || dp[i+1][j-1])){
11                     dp[i][j] = true;
12                     count++;
13                 }
14             }
15         }
16         return count;
17     }
18 }