【学习笔记】 - 基础数据结构 ：Link-Cut Tree(进阶篇)

前言

LCT没题写可以去写树剖和一些线段树合并的题练手

LCT 的概念

原本的树剖是对树进行剖分，剖分为重边和轻边

LCT则是对于树分为虚边和实边，特殊的，LCT可以没有虚边(例：银河英雄传说v2)

单独被包含在一个实链里的点称作孤立点

在树剖中，我们使用线段树/树状数组来维护重链

在Link-Cut Tree里我们使用一种更灵活地数据结构splay来维护这些实链

splay维护的是所有实边路径的中序遍历

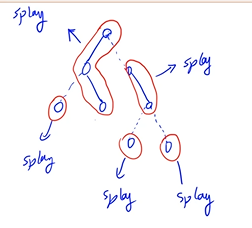
每个实链都是一颗splay

每条实链之间都有一条虚边将其连接起来

x 的子节点其实是 x 在 splay 里的后继节点，而 x 的父节点其实是 x 在 splay 里的前驱节点

注意，这里 splay 本身也有父节点和子节点，但是 splay 里的父节点和子节点与原树的父节点和子节点没有任何关系

虚边用每个 splay 的根节点来维护

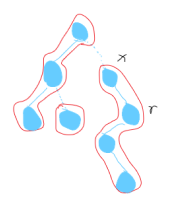
如下图，假设这里的右侧包含 x 和 r 节点的整颗 splay 的根节点为 r，则虚边应该在splay中记录为 r 的父节点，而非 x 的父节点

我们发现，对于虚边而言，子节点能够指向父节点，父节点却不知道子节点是谁

也就是说，路径用 splay 来维护，而路径与路径的关系用 splay 的根节点来维护

我们可以非常简单的把一条实边删掉，换成一条虚边，只要把父节点的后继修改即可

---

LCT 的基本操作

这里可以直接接上前面的学习笔记了

这里是上一篇

发现树剖代码太长了，给我恶心坏了

学个代码短点的能写树剖题的数据结构吧

前置知识

• 平衡树splay

• 树链剖分

简介以及优缺点介绍

Link-Cut Tree，也就是LCT，一般用于解决动态树问题

Link-Cut Tree可用于实现重链剖分的绝大多数问题，复杂度为\(O(n \log n)\)，看起来比树剖的\(O(n \log^2 n)\)复杂度更小，但则不然，基于splay实现的Link-Cut Tree常数巨大(约11倍常数)，往往表现不如树剖

Link-Cut Tree的代码往往比树剖少一些

动态树问题

维护一个森林，支持删除某条边，连接某条边，并保证加边/删边之后仍是森林

同时维护这个森林的一些信息

实链剖分

• 回顾重链剖分

  • 按子树大小剖分整棵树并重新标号

  • 此时树上形成了一些以链为单位的连续区间，用线段树进行区间操作

我们发现，诶重剖怎么是按子树大小来剖的，这也不能搞动态树啊

显然我们需要让剖分的链是我们指定的链，以便利用来求解

• 实链剖分

  对于一个点连向它所有儿子的边，我们自己选择一条边进行剖分，我们称被选择的边为实边，其他边则为虚边。

  我们称实边所连接的儿子为实儿子，实边组成的链称之为实链

  选择实链剖分的最重要的原因便是因为实链是我们选择的，灵活且可变

  正是它的这种灵活可变性，用 Splay 来维护这些实链

Link-Cut Tree

我们可以把 LCT 理解为用一些 Splay 来维护动态树剖并实现动态树上的区间操作

每条实链都建一个 Splay 维护整个链的区间信息

• 辅助树

  我们认为一些 Splay 共同构成了一颗辅助树，每个辅助树都维护了一颗树，所有的辅助树构成了 Link-Cut Tree，维护了整个森林

  辅助树有很多性质

  • 辅助树由多棵 Splay 组成，每棵 Splay 都维护了树中一条严格在原树中「从上到下」深度单调递增的路径，且中序遍历这棵 Splay 得到的点的深度序列单调递增

  • 原本的树的每个节点与辅助树的 Splay 节点一一对应。

  • 辅助树各棵 Splay 间并不独立。在 LCT 中每棵 Splay 的根节点的父亲节点指向原树中这条链的父亲节点（即链最顶端的点的父亲节点）。

    特殊的，这里的儿子认父亲，父亲却不认儿子，对应原树的一条 虚边

    故每个连通块恰好有一个点的父亲节点为空

  • 维护任何操作都不需要维护原树

    辅助树可以在任何情况下拿出一个唯一的原树

    只需维护辅助树即可

  这是一颗原树 \(\gets\)

  这是建出的辅助树 \(\gets\)

代码实现

这里只有 LCT 特有的几个操作

• 数组定义

  fa[x] //x的父亲节点
  son[x][2] //x的左右儿子
  sz[x] //x的子树大小
  rev[x] //x是否需要对儿子进行翻转
  

• splay操作

  和正常splay不同的是LCT的每次splay影响的所有点都必须是当前splay中的钱

  而且在splay操作前必须把它的所有祖先全都pushdown，因为LCT不一定把哪个点应用splay操作

  • 代码

    inline bool isroot(int x){
        return ((son[fa[x]][0]==x)||(son[fa[x]][1]==x));
    }
    inline void splay(int x){
        int y=x,z=0;
        st[++z]=y;
        while(isroot(y)){
            st[++z]=y=fa[y];
        }
        while(z){
            push_down(st[z--]);
        }
        while(isroot(x)){
            y=fa[x],z=fa[y];
            if(isroot(y))
                rotate((son[y][0]==x)^(son[z][0]==y)?x:y);
            rotate(x);
        }
        push_up(x);
    }
    

• access操作

  LCT最重要的操作，其他所有操作都要用到它

  含义是访问某节点，作用是对于访问的节点 \(x\) 打通一条从树根到 \(x\) 的实链

  如果有其他实边与新的实链相连则改为轻边

  可以理解为专门开辟一条从 \(x\) 到 \(root\) 的路径，用splay来维护这条路径

  • 实现方法

    先把 \(x\) 旋转到所在Splay的根

    用 \(y\) 记录上一次的 \(x\) (初始化\(y=0\))，把 \(y\) 接到 \(x\) 的右儿子上

    这样就把上一次的实链接到了当前实链下

    它原来的右儿子(也就是LCT树中在 \(x\) 下方的点)与它所有的边自然变成了虚边

    记得pushup

  • 代码

    inline void access(int x){
        for(int y=0;x;x=fa[y=x])
            splay(x),
            rc=y,push_up(x);
    }
    

• 换根操作

  作用是把某个节点变成树根(这里的根指的是整颗LCT的根)

  再加上access操作就能方便的提取出LCT上两点之间距离

  提取\(u\)到\(v\)的路径只需要toroot(u),access(v)，然后\(v\)所在的Splay对应的链就是\(u\)到\(v\)的路径

  • 实现方法

    先 access 一下，这样 \(x\) 就一路打通到了根，然后再splay(x)，由于x是这条实链最下面的点，所以 \(x\) 的 splay 的右儿子是空的，左儿子是它上面所有点

    因为 splay 是支持区间翻转的，所以只要给x打个翻转标记就翻转到根了

  • 代码

    inline void toroot(int x){
        access(x);
        splay(x);
        reserve(x);
    }
    

• link操作

  作用是链接两个辅助树，对于link(u,v)，表示 \(u\) 所在的辅助树和 \(v\) 所在的辅助树

  • 实现方法

    只需要先toroot(u)，然后记 fa[u]=v 就可以了，就是把一整颗辅助树连到另一个点上

  • 代码

    inline void link(int x,int y){
        toroot(x);
        if(Find(y)!=x)
            fa[x]=y;
    }
    

• cut操作

  这个操作作用是切断某条边

  • 实现方法

    先分离出 \(x\) 到 \(y\) 的这条链

    我们假设切断的点一定是相邻的(不相邻的特判掉)，然后把 \(y\) 的左儿子(也就是 LCT 中 \(y\) 的父亲)与 \(y\) 的边断掉就好了

  • 代码

    inline void split(int x,int y){
        toroot(x);
        access(y);
        splay(y);
    }
    inline int Find(int x){
        access(x);
        splay(x);
        while(lc)
            push_down(x),x=lc;
        splay(x);
        return x;
    }
    inline void cut(int x,int y){
        toroot(x);
        if(Find(y)==x&&fa[y]==x&&!son[y][0]){
            fa[y]=son[x][1]=0;
            push_up(x);
        }
    }
    

完整代码

模板题

点击查看代码

#define lc son[x][0]
#define rc son[x][1]
int fa[N],son[N][2],val[N],ans[N],st[N];
bool rev[N];
inline bool isroot(int x){
    return ((son[fa[x]][0]==x)||(son[fa[x]][1]==x));
}
inline void push_up(int x){
    ans[x]=ans[lc]^ans[rc]^val[x];
}
inline void reserve(int x){
    int t=lc;
    lc=rc;rc=t;
    rev[x]^=1;
}
inline void push_down(int x){
    if(rev[x]){
        if(lc)reserve(lc);
        if(rc)reserve(rc);
        rev[x]=0;
    }
}
inline void rotate(int x){
    int y=fa[x],z=fa[y],k=son[y][1]==x,w=son[x][!k];
    if(isroot(y))
        son[z][son[z][1]==y]=x;
    son[x][!k]=y;
    son[y][k]=w;
    if(w)
        fa[w]=y;
    fa[y]=x;fa[x]=z;
    push_up(y);
}
inline void splay(int x){
    int y=x,z=0;
    st[++z]=y;
    while(isroot(y)){
        st[++z]=y=fa[y];
    }
    while(z){
        push_down(st[z--]);
    }
    while(isroot(x)){
        y=fa[x],z=fa[y];
        if(isroot(y))
            rotate((son[y][0]==x)^(son[z][0]==y)?x:y);
        rotate(x);
    }
    push_up(x);
}
inline void access(int x){
    for(int y=0;x;x=fa[y=x])
        splay(x),
        rc=y,push_up(x);
}
inline void toroot(int x){
    access(x);
    splay(x);
    reserve(x);
}
inline int Find(int x){
    access(x);
    splay(x);
    while(lc)
        push_down(x),x=lc;
    splay(x);
    return x;
}
inline void split(int x,int y){
    toroot(x);
    access(y);
    splay(y);
}
inline void link(int x,int y){
    toroot(x);
    if(Find(y)!=x)
        fa[x]=y;
}
inline void cut(int x,int y){
    toroot(x);
    if(Find(y)==x&&fa[y]==x&&!son[y][0]){
        fa[y]=son[x][1]=0;
        push_up(x);
    }
}
signed main(){
    int n,m;FastI>>n>>m;
    for(int i=1;i<=n;++i)
        FastI>>val[i];
    while(m--){
        int opt,x,y;
        FastI>>opt>>x>>y;
        if(opt==0){
            split(x,y);
            FastO<<ans[y]<<endl;
        }
        else if(opt==1){
            link(x,y);
        }
        else if(opt==2){
            cut(x,y);
        }
        else if(opt==3){
            splay(x);
            val[x]=y;
        }
    }
}

---

进阶一点的操作/配套题目

• P1501 [国家集训队] \(\text{Tree II}\)

  依然是链操作，但是有区间加法和区间乘法操作

  这里参考了动态树大师FlashHu的题解

  • 区间加法

    先用 spilt 操作把 x 到 y 的链分离出来

    然后整体直接加上 lazy 标记即可，并且在pushdown操作时额外加入推平操作即可

    核心代码也很简单

    inline void push_add(int x,int c){
        (val[x]+=c*sz[x])%=51061;
        (v[x]+=c)%=51061;
        (lazy_add[x]]+=c)%=51061;
    }
    

    在pushdown操作翻转前加入以下代码

    if(lazy_add[x]){
        push_add(lc,lazy_add[x]),
        push_add(rc,lazy_add[x]),
        lazy_add[x]=0;
    }
    

  • 区间乘法

    也是先用 spilt 操作分离,然后挂 lazy 标记，pushdown 操作加入乘法标记

    注意要先 pushdown 乘法的 lazy 标记，再 pushdown 加法的

    核心代码

    inline void push_mul(int x,int c){
        (val[x]*=c)%=51061;
        (v[x]*=c)%=51061;
        (lazy_mul[x]*=c)%=51061;
        (lazy_add[x]*=c)%=51061;
    }
    

    在pushdown操作内pushdown加法前加入以下代码

    if(lazy_mul[x]!=1){
        push_mul(lc,lazy_mul[x]),
        push_mul(rc,lazy_mul[x]),
        lazy_mul[x]=1;
    }
    

  那么就非常好搞了

  核心代码都在上面了

• P3950 部落冲突

  维护两点是否连通，但是包含了断边操作和连边操作

  这样普通的并查集就不好维护了，但是可以考虑使用 LCT 来维护

  维护方法就是直接对两点进行 Find ，如果 Find 的结果相同那就是联通的

  • 核心代码

    if(opt=="Q"){
        FastO<<((Find(x)==Find(y))?"Yes":"No")<<endl;
    }
    

• P2147 [SDOI2008] 洞穴勘测

  和上一题是双倍经验，基本区别不大

  核心代码和上面一样

• [POJ3237] 树的维护

  这道题与一般的 LCT 似乎有一点不同

  给的不是点权，那怎么办呢

  错误思考示范

  诶树剖的时候好像也有这个问题，是不是可以参考树剖

  用儿子节点记录其到其父亲的边权，然后云云

  但是这样有个问题，就是说 LCT 使用 splay 维护的，splay 是会破坏原本的父子关系的

  那么这个做法宣告破产了wwwww

  根据 FalshHu 的讲解，我们可以得知有两种解法

  1. 把边置于 LCT 外，然后在 LCT 节点中维护父边和重子边的编号，需要更新信息时从外部获取

     但是这种方法有一个问题：需要在access操作，Link操作，Cut操作都进行修改，很麻烦

  2. 建立额外的节点

     我们可以建立额外的表示边的节点，然后把表示点的节点的权值都设为\(0\)

     这样我们就可以把原本的边权转化为点权来让 LCT 去维护

     此时普通的 Link 和 Cut 都存在一些问题

     Link 和 Cut 操作只能添加/删除一条边，而不能删除代表边权的边

     解决方法也很简单，直接 Link/Cut 两次即可

     • 核心代码

       link(a[i].x,a[i].id);
       link(a[i].id,a[i].y);
       

  我们通常选择建立代表边的节点，也就是第二种方法

  在本题中建立边的方式如下

  for(int i=1;i<n;++i){
      FastI>>x>>y>>val[i+n];
      link(x,i+n);
      link(y,i+n);
  }
  

  这里的求 max 后取反如何维护呢？我们发现只要取 min 即可，这样取相反数后的结果就是 max

  那么这道题就非常容易的做出来了

• P4114 Qtree1

  树剖板子题，不用LCT也能写但是这里用的LCT

  需要边权转点权

• P4172 [WC2006] 水管局长

  • 不断加边，判环，取较优者。

  LCT 动态维护生成树(边权的最大值最小)，似乎不是很好维护删边(因为不能对于每次删除都进行一次最小生成树，不然复杂度爆炸了)

  但是本题只有删边操作，所以我们可以先对操作离线，然后倒过来变为加边

  先把所有边都删掉，这里保证了任何时刻图都是联通的，所以就可以来离线完成

  如何加入边呢

  在加入一条边之后会形成一个环，此时从任意一点进入环，从另一点出环，可以从环上两个方向走，那么最优解总可以避开最长的一条边

  我们先split(x,y)提取出 x 到 y 的最大权值，然后看加入的边，如果比原来的最大权值小就可以直接断掉原来的最大权值那条边

  这里直接平衡树查找就行，所以我觉得map更好做其实

  在倒序跑完最小生成树之后就可以直接维护了

  for(int i=q-1;i>=0;--i){
      int x=vec[i].a,y=vec[i].b;
      split(x,y);
      if(vec[i].k==1){
          sta.push(T[ans[y]].val);
      }
      else{
          if(T[vec[i].num].val<T[ans[y]].val){
              cut(T[ans[y]].s,j+n);
              cut(ans[y]+n,T[ans[y]].son);
              link(x,vec[i].num+n);
              link(vec[i].num+n,y);
          }
      }
  }
  

  这里的sta用于记录答案

• P4219 [BJOI2014] 大融合

  坏了，要维护子树的siz了，我们优秀的LCT只能比较容易的维护链信息而弱于子树信息

  但是还要动态加边所以要用LCT，不太能直接树剖

  所以我们需要对LCT进行一定修改使其适于子树操作

  我们按照对链剖分的方式把子树分为虚子树和实子树，其中实子树就是一条实链，可以直接通过 splay 获取

  那么瓶颈主要就在虚子树上(因为已知实子树的信息，只要知道虚子树的信息和就可以求出整个子树的信息了)

  我们这里设虚子树siz为si[x]，整棵子树的siz为s[x]

  考虑对原本的操作进行修改

  • splay操作

    这一操作基于splay树且只会修改在splay树中的相对位置，众所周知splay树中的相对位置对于虚子树是不会有任何影响的，所以不需要修改

  • access操作

    access操作的含义是作用是对于访问的节点 \(x\) 打通一条从树根到 \(x\) 的实链

    然后会修改实边虚边，所以会对虚子树产生影响，得到一个虚儿子，失去一个虚儿子

    直接改就行

    inline void access(int x){
        for(int y=0;x;x=fa[y=x]){
            splay(x);
            si[x]+=s[rc];
            si[x]-=s[y];
            rc=y;
            pushup(x);
        }
    }
    

    和普通 access 操作的对比

    这是普通的access

    inline void access(int x){
        for(int y=0;x;x=fa[y=x]){
            splay(x);
            rc=y;
            pushup(x);
        }
    }
    

    不同点只是si加上原来右儿子的s，再减去新的右儿子的s

  • toroot操作

    换根，但是我们发现toroot只是在实链上的翻转，所以对虚子树没有影响

    不用改

  • findroot操作

    这显然没影响，并没有改变树的形态

  • split操作

    分离操作

    这里实现时只是调用了toroot(x),access(y),splay(y);三个函数

    而有影响的access操作我们已经在前面改了，所以这个没有影响

  • link操作

    连边操作

    当连接一条边时，虚子树的信息会发生改变(因为多了一个虚边)

    那么s[y]和si[y]都加上s[x]就行

    但是这里只更新了y，y的祖先没更新，所以会寄

    只要先把y转到根，这样y就没祖先了

    inline void link(int x,int y){
        toroot(x);access(y);splay(y);
        fa[x]=y;si[y]+=s[x];
        pushup(y);
    }
    

  • cut操作

    断边操作

    cut操作会断掉一条实边，不会影响虚子树，建议不理

  • pushup操作

    这个直接把虚子树和实子树加起来就行

    inline void pushup(int x){
        s[x]=s[lc]+s[rc]+si[x]+1;
    }
    

  回过头来看这道题，发现这是板子

  对于操作2，询问的是断掉(x,y)之后x和y的子树大小乘积

  直接做就行

  • 核心代码

    if(opt=='A'){
        link(x,y);
    }
    else{
        cut(x,y);
        FastO<<(s[x])*(s[y])<<endl;
        link(x,y);
    }