IEEE754浮点数表示形式

IEEE754浮点数表示形式

IEEE754浮点数官方文档：https://ieeexplore.ieee.org/document/8766229

• 浮点数的上述表示形式，既没有规定阶码和尾数的位数，也没有规定阶码和尾数采用的机器码形式（原码、反码、补码和移码）。实际上，直到20世纪80年代初，浮点数表示形式还没有统一标准，不同厂商计算机内部浮点数表示形式可能不同。

• 不同体系结构的计算机之间进行数据传送或程序移植时，必须进行数据格式的转换，并且数据格式转换还会带来运算结果的不一致。因此，美国电气及电子工程师协会(Institute of Electrical and Electronics Engineers,IEEE)于1985年发布 了浮点数标准IEEE754。

• 目前，几乎所有计算机都采用IEEE 754标准表示浮点数。

IEEE754标准主要包括两种基本的浮点数格式：

• 32位单精度浮点数，对应C语言中的float型。

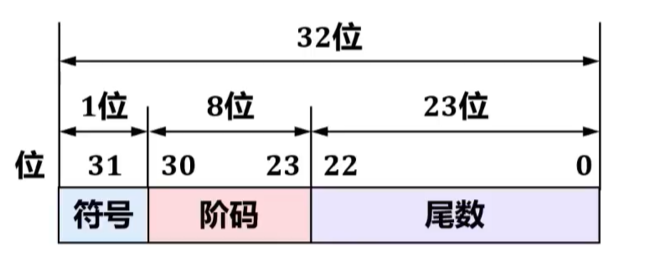
其中：

1. 符号：取值0表示正数；取值1表示负数。
2. 阶码：定点整数，用移码表示。
3. 尾数：定点小数，用原码表示。

• 64位双精度浮点数，对应C语言中的double型。

回顾一下移码定义：

假设真值x为定点整数，n为x的移码表示中数值位的位数（比特数量）。[x]移=x+\(2^{n}\)， -\(2^{n}\)≤x<\(2^{n}\)

移码的优点：

• 最小真值的移码为全0，最大真值的移码为全1，符合人们的习惯。
• 真值0在移码中只有一种表示。
• 移码保持了真值原有的大小顺序，可以直接比较大小。
• 当浮点数的阶码用移码来表示时，就能很方便地比较阶码的大小。
• 不考虑移码的符号位看作无符号二进制数

[x]移=x+\(2^{n}\)， -\(2^{n}\)≤x<\(2^{n}\)

[x]移=x+\(2^{7}\)， -\(2^{7}\)≤x<\(2^{7}\)

在IEEE754浮点数标准中，32位单精度浮点数的8位阶码尽管采用移码表示，但采用偏移常数是\(2^{7}\)-1=127，而不是标准移码的\(2^{7}\)=128。

[x]移=x+(\(2^{7}\)-1)， -\(2^{7}\)≤x<\(2^{7}\)

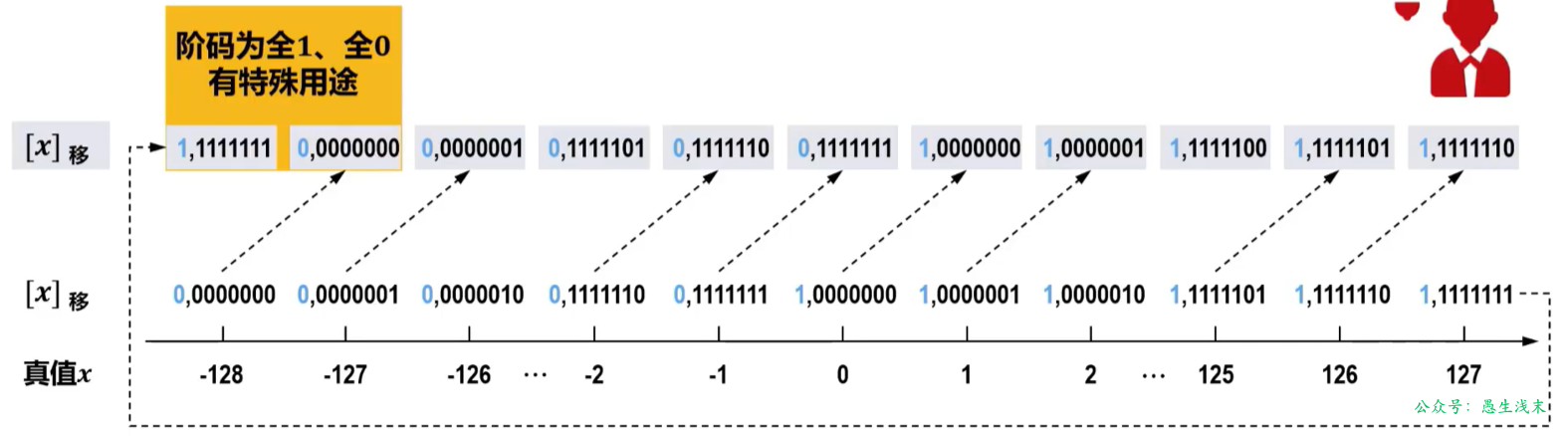
为什么偏移常数不采用标准的128，而采用127？

采用偏移常数128表示的最小规格化数的倒数会发生溢出，而采用偏移常数127表示的任何一个规格化数的倒数则不会溢出。

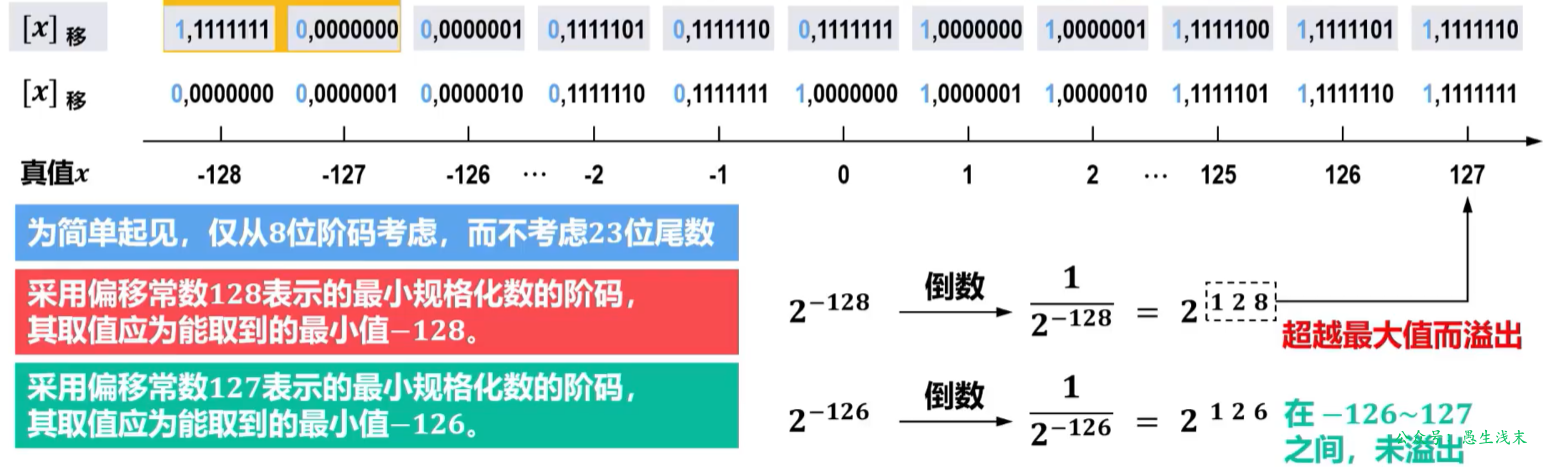
下面以32位单精度浮点数为例介绍IEEE754单精度浮点数标准:

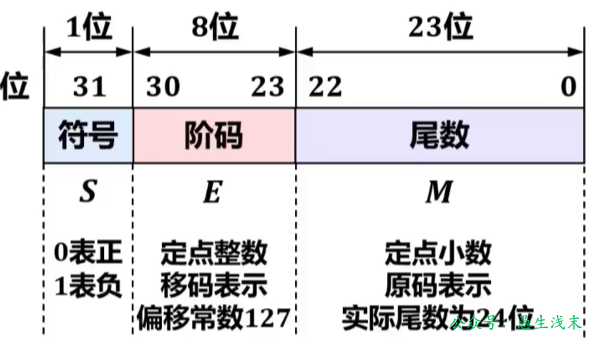
• 符号：取值0表示正数；取值1表示负数。
• 阶码：定点整数，用移码表示，偏置常数27—1=127。
• 尾数：定点小数，用原码表示。符号位前移到最左侧。相邻左侧隐藏一个1，表示数值而不表示符号。尾数实际有24位，但不保存隐藏的那个1，只保存23位，节省的比特位可用于提高尾数的精度。完整的尾数形式为1.M

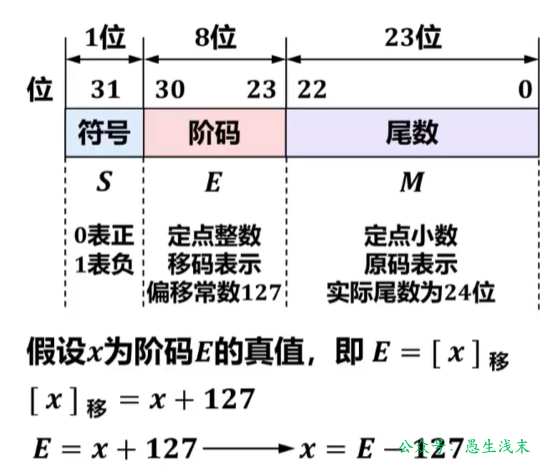
32位浮点数标准示意如下：

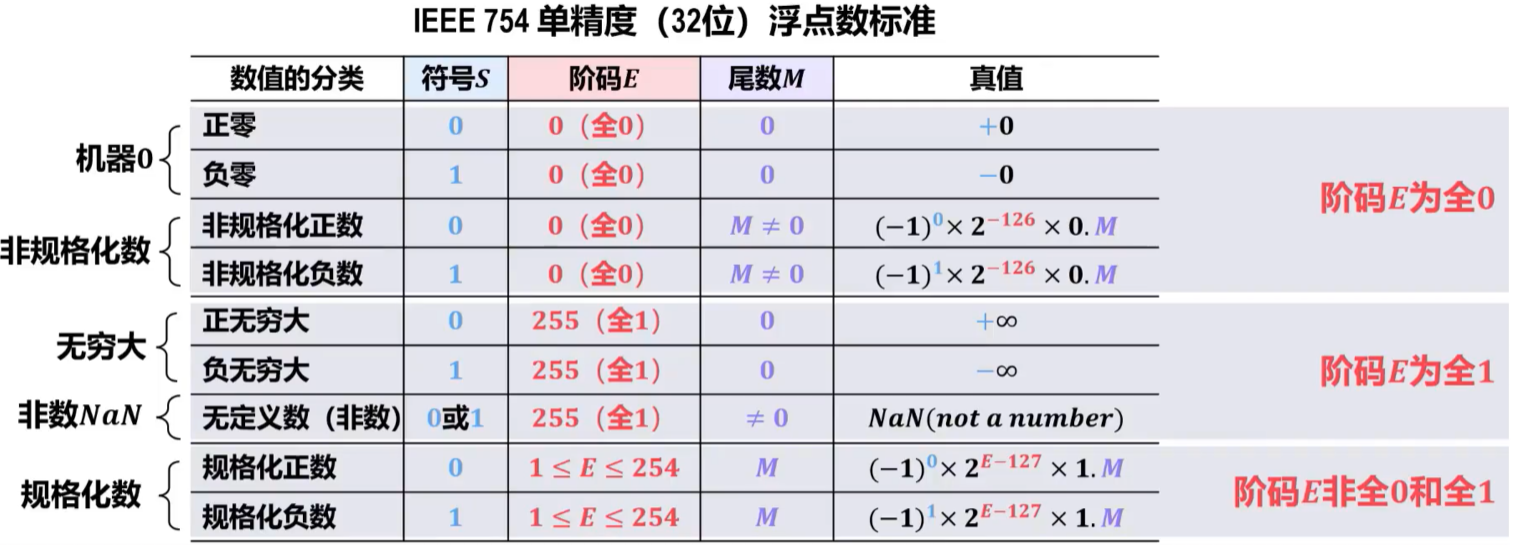
• 非数NaN用于表示\(\frac {0}{0}\)、\(\frac {∞}{∞}\)、0×∞、负数的平方根等。部分非数NaN运算结果可能会产生异常。
• 非规格化数可用于处理阶码下溢，使得出现比最小规格化数还小的数时程序也能继续进行下去。
• 引入无穷大数可使计算过程出现异常的情况下程序能继续执行，并且可为程序提供错误检测功能。例如非0浮点数除0运算的结果就是无究大，因此非0浮点数除不会像整型数除0一样产生严重错误。

32位浮点数和64位浮点数对比：

【例题1】将十进制数408.6875转换成IEEE754单精度浮点数的十六进制机器码。

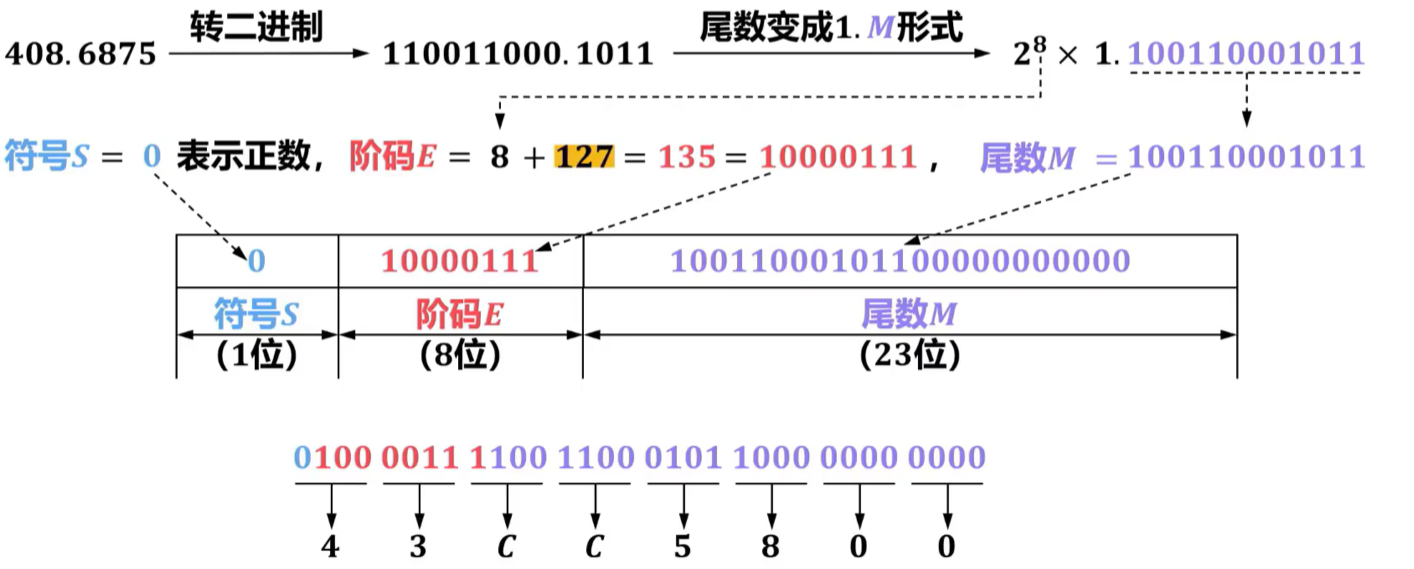
【例题2】若C1830000是某个IEEE754单精度浮点数的十六进制机器码，求其对应的十进制值。

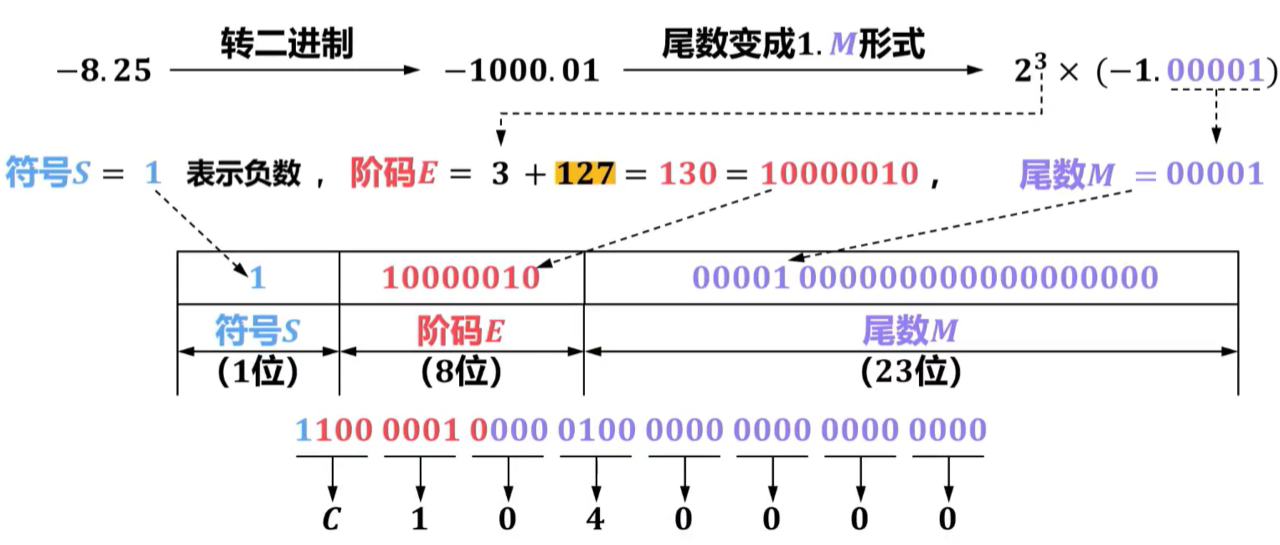
【2011年题13】float型数据通常用IEEE 754单精度格式表示。若编译器将float型变量x分配一个32位浮点寄存器FR1中，且x=—8.25，则FR1的内容是（A）。

A. C104 0000H

B. C242 0000H

C. C184 0000H

D. C1C2 0000H

【2013年题13】某数采用IEEE754单精度浮点数格式表示为C640000H，则该数的值是（A）。

A. -1. 5× \(2^{13}\)

B.-1.5× \(2^{12}\)

C.-0. 5 × \(2^{13}\)

D.-0.5×\(2^{12}\)

【2014年题14】float型数据常用IEEE 754单精度浮点格式表示。假设两个float型变量x和y分别存放在32位寄存器f1和f2中，若(f1)=CC900000H,(f2)=B0C00000H, 则x和y之间的关系是（A）。

A.x<y且符号相同

B.x<y且符号不同

C.x>y且符号相同

D.x>y且符号不同

【2022年 题14】—0.4375的IEEE754单精度浮点数表示为(A)

A. BEEO 0000H

B. BF60 0000H

C. BF70 0000H

D. COEO 0000H

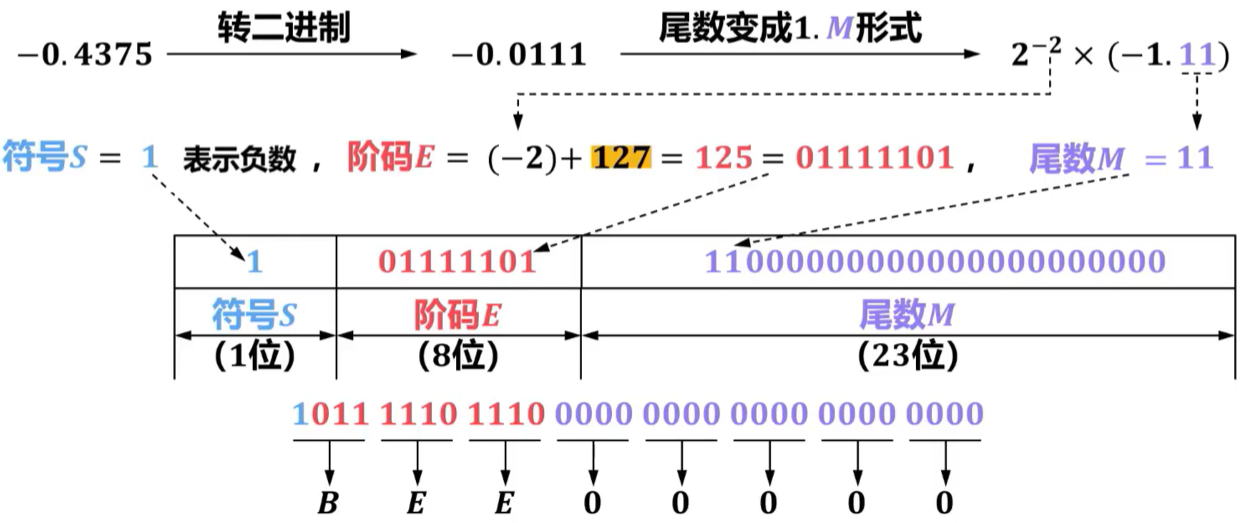
IEEE754单精度（32位）浮点数表示范围:

【2012年题14】float类型（即IEEE754单精度浮点数格式）能表示的最大正整数是（D）。

A. 2126- 2103

B.2127-2104

C. 2127- 2103

D.2128-2104

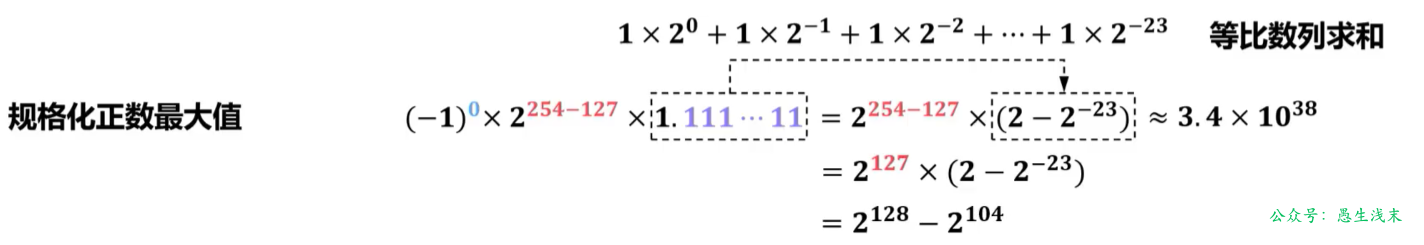
【2018年题14】IEEE754单精度浮点格式表示的数中，最小的规格化正数是（A）。

A. 1.0 X \(2^{-126}\)

B. 1. 0 X \(2^{-127}\)

C. 1. 0 X \(2^{-128}\)

D.1.0×2\(2^{-149}\)

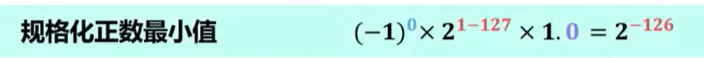
【2021年题14】下列数值中，不能用IEEE754浮点格式精确表示的是（A）。

A. 1. 2

B. 1. 25

C. 2.0

D. 2. 5

对于无限循环小数，通常只能采用舍入的方式近似表示，因此会带来数据表示的误差。这种误差会在计算的过程中不断累积放大，可能导致严重后果。

综上所述，程序员使用二进制浮点数编程时一定要非常小心，要充分考虑浮点数运算可能带来的计算误差，尽量避免对浮点数进行直接比较，在一些对误差极其敏感的情况下，建议采用十进制浮点数进行运算。

IEEE754其他浮点数标准：

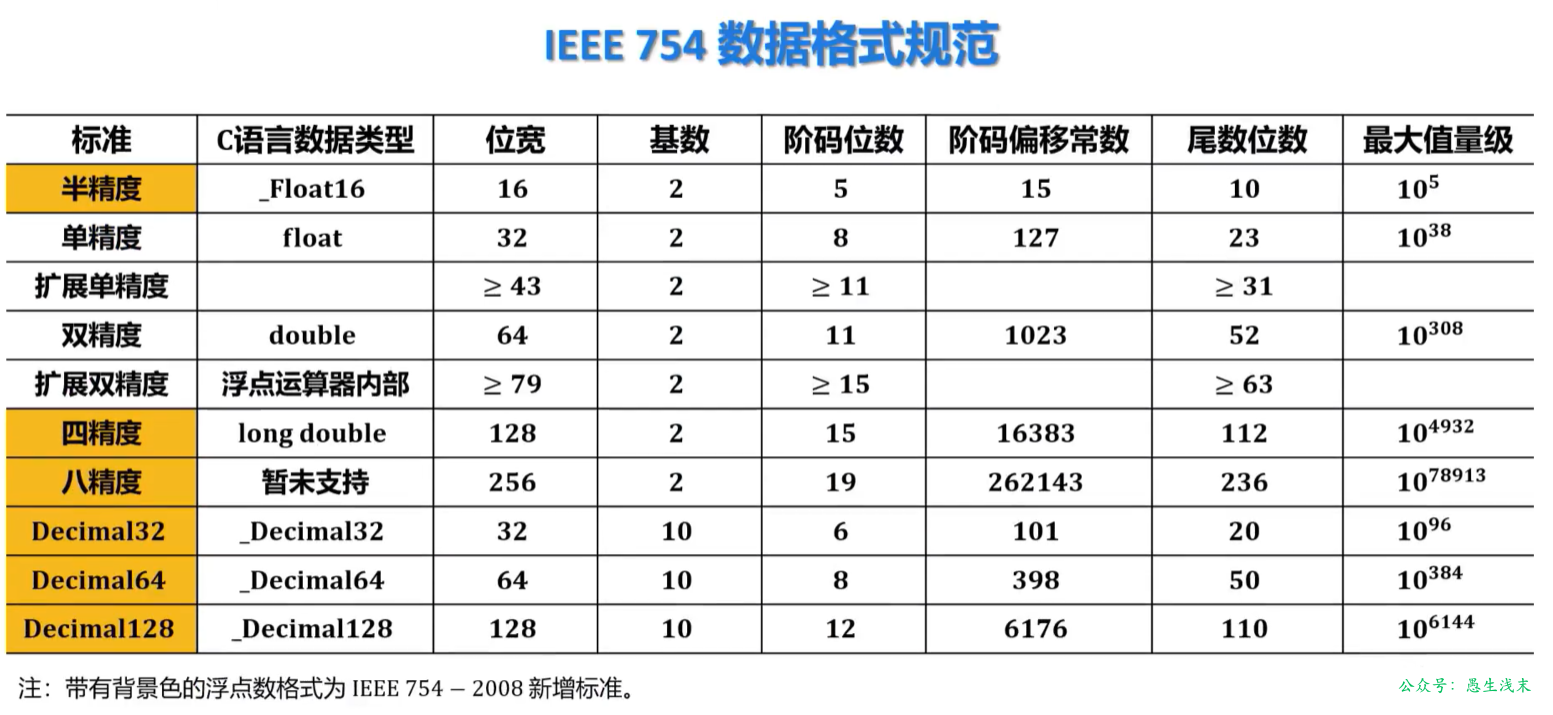
推荐阅读：

• 计算机基础知识之原码、补码、反码和移码
• 计算机基础知识之浮点数的表示

欢迎关注公众号：愚生浅末