【matlab混沌理论】1.3.双摆杆基本模型
双摆杆是混沌理论的典型运动模型之一。涉及重力加速度、摆杆长度和质量。

1.双摆杆的摆角分析
input:
% 已知物理参数
L1 = 5;L2 = 3; %两摆杆长度和质量
m1 = 3;m2 = 5;
g = 9.80665; % 物理重力加速度m/s^2 % 定义初始参数
% y0的第1参数,即摆1的初始角度;第2,即摆2的初始角度
% 第3,摆1的初始角速度;第4,摆2的初始角速度
theta1_0 = pi/2;
theta2_0 = pi/2;
%警告: 在 t=2.623401e+00 处失败。在时间 t 处,步长必须降至所允许的最小值(7.105427e-15)以下,才能达到积分容差要求。
tspan = [0,0.01,2];
doublePendulum(tspan,theta1_0,theta2_0,L1,L2,m1,m2,g); function [T, Theta1, Theta2] = doublePendulum(tspan,theta1_0,theta2_0,L1,L2,m1,m2,g)
% 定义求解常微分方程所需的函数
function dydt = doubleP(t,y)
% 定义双摆模型方程
d1 = m1+m2*L1^2/L2^2;
d2 = m2*L1*L2*cos(y(1)-y(2))/L2^2;
d3 = m2*L1*L2*sin(y(1)-y(2))*y(4)^2/L2;
d4 = g/L2*sin(y(2)) + cos(y(1)-y(2))*y(3)^2/L2;
dydt = [y(3); y(4); (m2*d4*d2-d3*m2*cos(y(1)-y(2)))/(d1-m2*d2*d2); (d1*d4-m2*d3*cos(y(1)-y(2)))/(L2*(d1-m2*d2*d2))];
end
% 定义初值和时间步长
y0 = [theta1_0, theta2_0, 0, 0];
options = odeset('RelTol',1e-10,'AbsTol',1e-10); % 调用ode45求解微分方程组
[T,Y] = ode45(@doubleP,tspan,y0,options); % 计算摆的位置
Theta1 = L1*sin(Y(:,1));
Theta2 = L2*sin(Y(:,2))+Theta1;
Theta1 = -L1*cos(Y(:,1));
Theta2 = -L2*cos(Y(:,2))+Theta2; % 绘制双摆摆角随时间变化的图像
plot(T,Y(:,1:2))
legend('\theta_1','\theta_2')
xlabel('时间 t')
ylabel('摆角 \theta')
title('双摆摆角随时间变化的图像')
end
output:
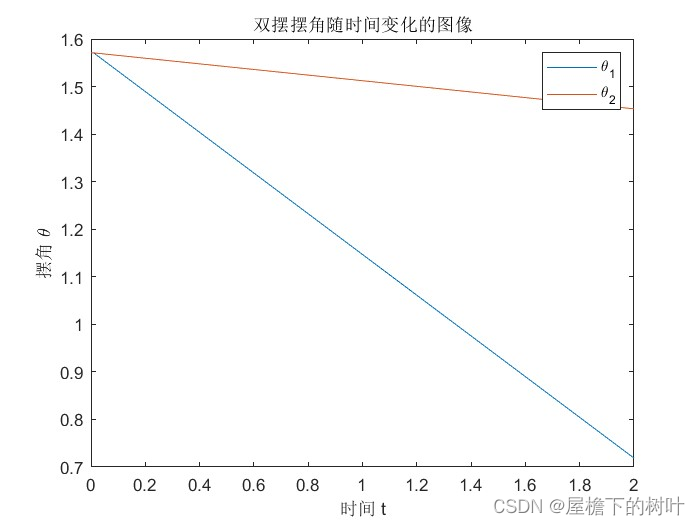
2.双摆杆基本运动模型
input:
% 运用双摆模型动画
% 初始角度
theta1 = pi/3;
theta2 = -pi/4; % 初始速度
w1 = 0;
w2 = 0; % 物理参数
g = 9.8; % 重力加速度
l1 = 3; % 第一根杆长度
l2 = 2; % 第二根杆长度
m1 = 2; % 第一个质点质量
m2 = 1; % 第二个质点质量 % 仿真时间
tmax = 10;
dt = 0.01;
tspan = 0:dt:tmax; % 初始状态
init = [theta1 w1 theta2 w2]; % 调用ode45求解微分方程
[t,y] = ode45(@(t,y)double_pend(t, y, m1, m2, l1, l2, g), tspan, init); % 动画绘制
figure('Name', '双摆动画');
for i = 1:length(t)
x1 = l1*sin(y(i, 1));
y1 = -l1*cos(y(i, 1));
x2 = x1+l2*sin(y(i, 3));
y2 = y1-l2*cos(y(i, 3));
plot([0;x1;x2], [0;y1;y2], '-o', 'LineWidth', 2);
axis([-3 3 -3 1]);
title(sprintf('双摆动画, t = %.2f', t(i)));
grid on;
drawnow;
end % 使用 animatedline 函数来动态绘制出双摆的运动轨迹
% 要调用这个double_pend函数,需要传入若干个参数(见上),包括时间 T,摆的位置 Theta1 与 Theta2,摆杆长度 L1 和 L2,以及每个时间步长的间隔时间 interval
function dydt = double_pend(t, y, m1, m2, l1, l2, g)
theta1 = y(1);
w1 = y(2);
theta2 = y(3);
w2 = y(4); dtheta1dt = w1;
dw1dt = (m2*g*sin(theta2)*cos(theta1-theta2)-m2*l1*w1^2*sin(theta1-theta2)-...
m2*l2*w2^2*sin(theta1-theta2)-(m1+m2)*g*sin(theta1))/((m1+m2)*l1-m2*l1*cos(theta1-theta2).^2);
dtheta2dt = w2;
dw2dt = ((m1+m2)*(g*sin(theta1)*cos(theta1-theta2)-l1*w1^2*sin(theta1-theta2)...
-g*sin(theta2))-m2*l2*w2^2*sin(theta1-theta2)*cos(theta1-theta2))/((m1+m2)*l2-m2*l2*cos(theta1-theta2).^2); dydt = [dtheta1dt; dw1dt; dtheta2dt; dw2dt];
end
output:
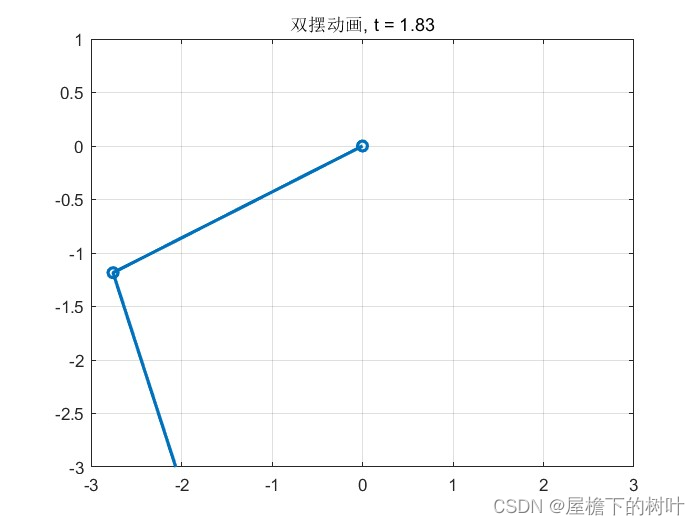
【matlab混沌理论】1.3.双摆杆基本模型的更多相关文章
- 混沌理论(Chaos theory)和非线性系统
混沌理论(Chaos theory)是关于非线性系统在一定参数条件下展现分岔(bifurcation).周期运动与非周期运动相互纠缠,以至于通向某种非周期有序运动的理论.在耗散系统和保守系统中,混沌运 ...
- Java 理论与实践: 修复 Java 内存模型,第 2 部分(转载)
在 JSR 133 中 JMM 会有什么改变? 活跃了将近三年的 JSR 133,近期发布了关于如何修复 Java 内存模型(Java Memory Model, JMM)的公开建议.在本系列文章的 ...
- 进程池与线程池基本使用、协程理论与实操、IO模型、前端、BS架构、HTTP协议与HTML前戏
昨日内容回顾 GIL全局解释器锁 1.在python解释器中 才有GIL的存在(只与解释器有关) 2.GIL本质上其实也是一把互斥锁(并发变串行 牺牲效率保证安全) 3.GIL的存在 是由于Cpyth ...
- MATLAB 机器人学工具箱(Robotics Toolbox )sl_drivepoint 模型 consecutive zero crossings 问题
操作环境 工具箱:Robotics Toolbox for MATLAB 版本 10.2.1 作者 Peter Corke MATLAB版本:R2018a 操作系统:win10 问题 sl_drive ...
- [ActionScript 3.0] AS3 双A字模型
package { import caurina.transitions.Tweener; import flash.display.Sprite; import flash.events.Mouse ...
- 《量化投资:以MATLAB为工具》连载(2)基础篇-N分钟学会MATLAB(中)
http://www.matlabsky.com/thread-43937-1-1.html <量化投资:以MATLAB为工具>连载(3)基础篇-N分钟学会MATLAB(下) ...
- 如何实现Linux+Windows双系统启动
设置你的计算机根据需要启动 Windows 10 或 Ubuntu 18.04. 尽管 Linux 是一个有着广泛的硬件和软件支持的操作系统,但事实上有时你仍需要使用 Windows,也许是因为有些不 ...
- 混沌数学之Chua's circuit(蔡氏电路)
蔡氏电路(英语:Chua's circuit),一种简单的非线性电子电路设计,它可以表现出标准的混沌理论行为.在1983年,由蔡少棠教授发表,当时他正在日本早稻田大学担任访问学者[1].这个电路的制作 ...
- 【转载】matlab常用函数
第一篇:Matlab软件函数 一.软件操作函数 1)命令窗口函数: clc:清空命令窗口,使用向上箭头翻看命令. open:打开文件,文本文件(*.doc),可执行文件(*.exe),图形文件(*.f ...
- MatLab 组件大全
MATLAB 矩阵实验室 7.0.1 Simulink ...
随机推荐
- 【路由器】小米 WR30U 解锁并刷机
本文主要记录个人对小米 WR30U 路由器的解锁和刷机过程,整体步骤与 一般安装流程 类似,但是由于 WR30U 的解锁 ssh 和刷机的过程中有一些细节需要注意,因此记录一下 解锁 ssh 环境准备 ...
- 程序员 不得不知道的 API 接口常识
说实话,我非常希望自己能早点看到本篇文章,大学那个时候懵懵懂懂,跟着网上的免费教程做了一个购物商城就屁颠屁颠往简历上写. 至今我仍清晰地记得,那个电商教程是怎么定义接口的: 管它是增加.修改.删除.带 ...
- 问题总结:浮点数之间的等值判断,基本数据类型不能用==来比较,包装数据类型不能用equals来判断
浮点数之间的等值判断,基本数据类型不能用==来比较,包装数据类型不能用equals来判断. 说明:浮点数采用"尾数+阶码"的编码方式,类似于科学计数法的"有效数字+指数& ...
- 「atcoder - 214G」Three Permutations
la traduction. link. 如果我们对于每一个 \(k\in[0,n]\) 找到所有满足存在 \(k\) 个 \(i\) 使得 \(r_i=p_i\) 或 \(r_i=q_i\) 条件的 ...
- RCU的简单认识
RCU RUC是什么? RCU(Read-Copy-Update)是一种用于并发编程的技术,旨在提供高效且无锁(lock-free)的读操作,同时保证数据一致性和并发性. 也就是说他并不需要锁的机制来 ...
- Redis——Redis面试题
文章目录 概述 什么是Redis Redis有哪些优缺点 为什么要用 Redis /为什么要用缓存 为什么要用 Redis 而不用 map/guava 做缓存? Redis为什么这么快 数据类型 Re ...
- js排序算法--冒泡排序
<!DOCTYPE html> <html> <head> <title></title> </head> <body&g ...
- 人工智能AI浪潮的掀起,打工人何去何从?
感谢你阅读本文 自从2022年11月30日OpenAI公司推出了ChatGPT,至今一年了,而这一年国内也发生了天翻地覆的变化,各大厂商纷纷推出了自己的大模型和解决方案,例如百度的文心一言,阿里的通义 ...
- 拒绝恶意IP登录服务器
拒绝恶意IP登录服务器,并加入防火墙黑名单 #!/bin/bash #2020-03-20 16:39 #auto refuse ip dlu #By Precious ############### ...
- 采药(lgP1048)
emmm 01 背包模板... 设 f[i] 表示背包容积为 i 时所得的最大价值. 则状态转移方程为 f[j] = f[j - w[i]] + c[i] . #include<bits/std ...
