[oeasy]python0045_四种进制_binary_octal_decimal_hexadecimal

四种进制

回忆上次内容

• 上次研究了

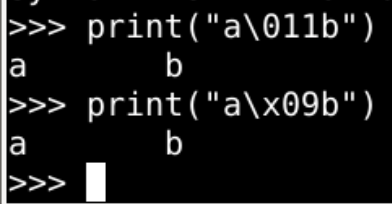
  • 通过 八进制数值 转义
    • \ooo
    • 把(ooo)_8进制对应的ascii字符输出

• 转义序列

  • \n、\t 是 转义序列
  • \xhh 也是 转义序列
  • \ooo 还是 转义序列

• 现在 总共有
  • 几种进制 了呢？
• 先数一下 树

数树

• 树 就是这么多棵树

• 用八进制的方式 数树

八进制

• 八根手指头
  • (13)_8进制棵

• 这是用 八根手指头 数的
  • 如果换成 十根手指头呢？

10进制

• 用十根手指头数树
  • (11)_10进制棵

• 到底多少棵树？
• 哪个才对呢？
  • (13)_8进制棵
  • (11)_10进制棵

数树

• 在不同进制下
  • 有不同的数值
  • 都是正确的

• 不同的进制
  • 只是表现形式 不同而已
  • 不会影响 树的数量
  • 本质 不变

表现形式

• 树 就是这么多棵 树

• 表示形式 不同
• 可以将数字 表示为
  • 二进制
  • 八进制
  • 十进制
  • 十六进制
• 为什么会有 各种进制形式 呢？

10进制、2进制、16进制

• 10进制
  • 是因为人的生理结构

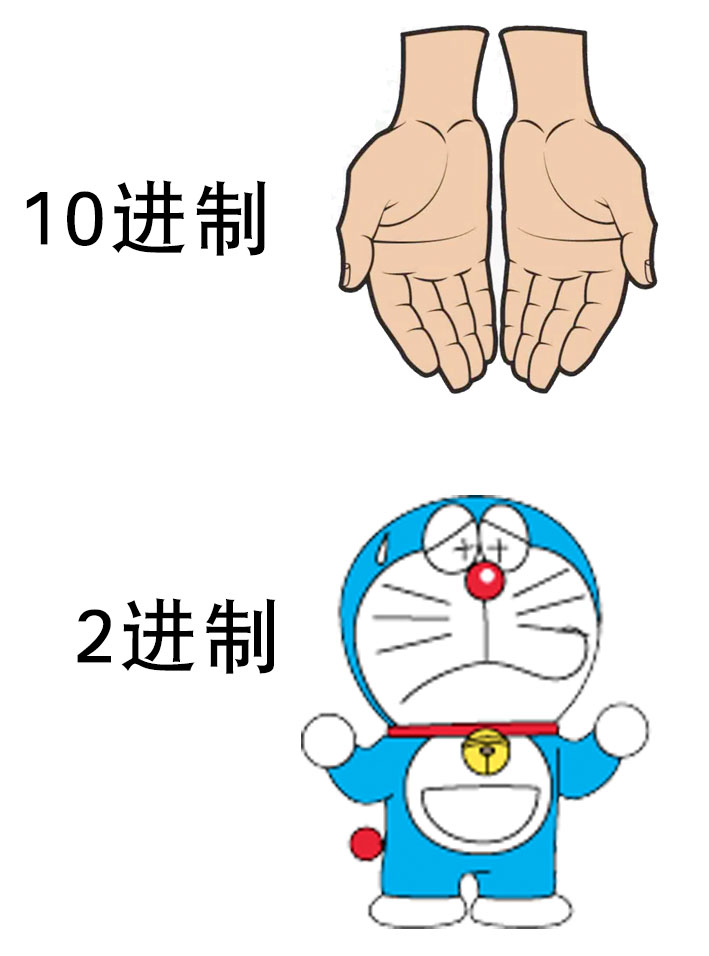
• 2进制
  • 电灯、开关等电器有两种状态
• 那为什么有16进制？
  • 难道说是因为有十六根手指？

16进制

• 16进制
  • 并不是因为
    • 谁 有十六根手指

• 而是因为
  • 可以用 两个16进制数字
    • 来描述字节状态

• 那为什么 会有八进制呢？
• 谁有 八根手指吗？

八进制

• 现实生活中的鸡
  • 一只脚 就有 四只脚趾
  • 大拇指在 最后面
• 一般飞禽
  • 每只脚都是 四只脚趾
  • 如果他们 有进制的话
  • 是八进制

• 除了鸭子
  • 鸭子天生就不适合数数

• 以上都为玩笑话…

输出字符

• 八进制
  • 方便输出字符

用纯数字的方式

• \ooo

• 这就是常见 的 各种进制

对应关系

• 不同数法
  • 不同结果

• 不同进制的词源如何？

二进制

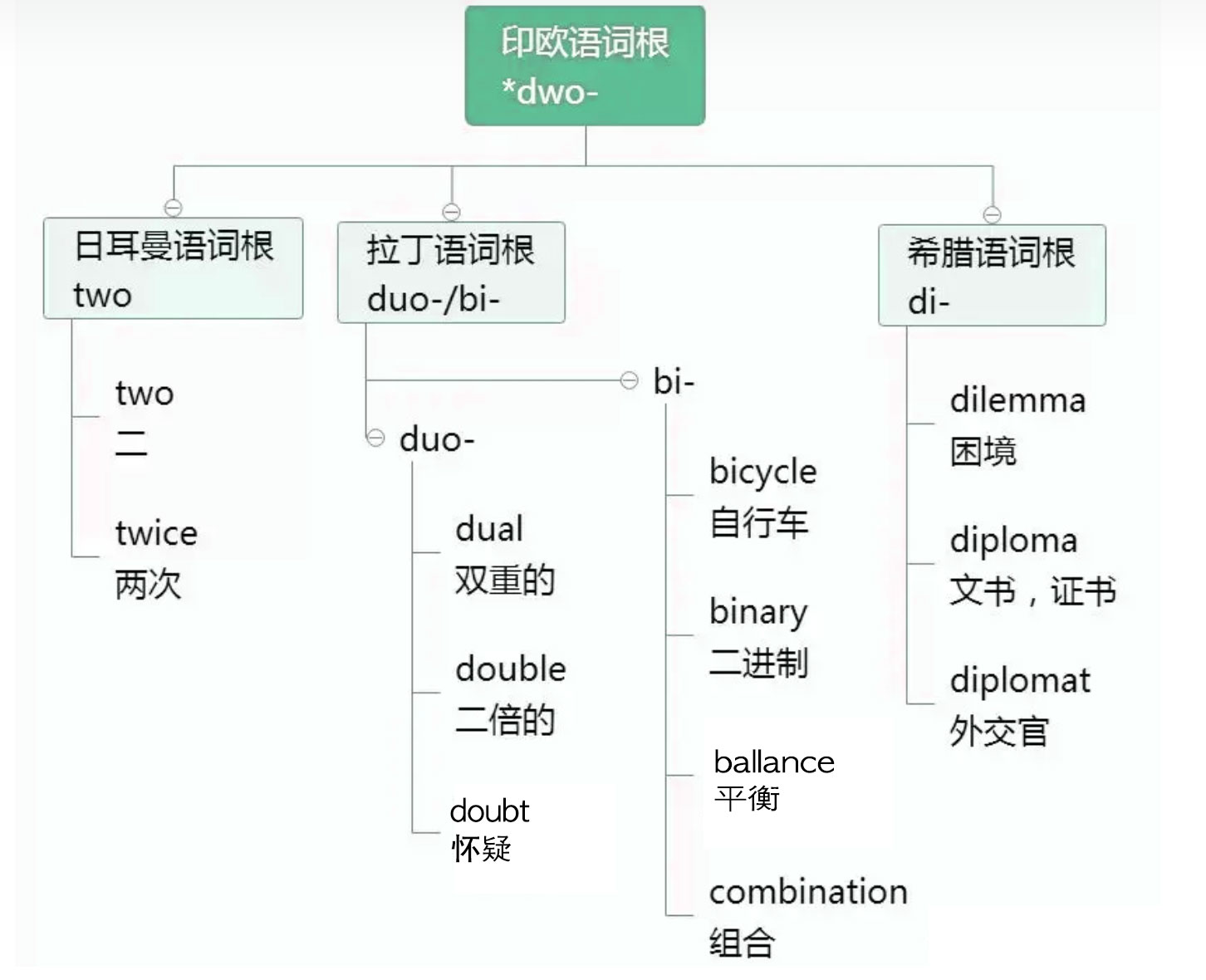
• *dwo-
  • two 日耳曼
  • duo- 拉丁
  • bi- 拉丁
  • di- 希腊

八进制

• octal
  • eight

十进制

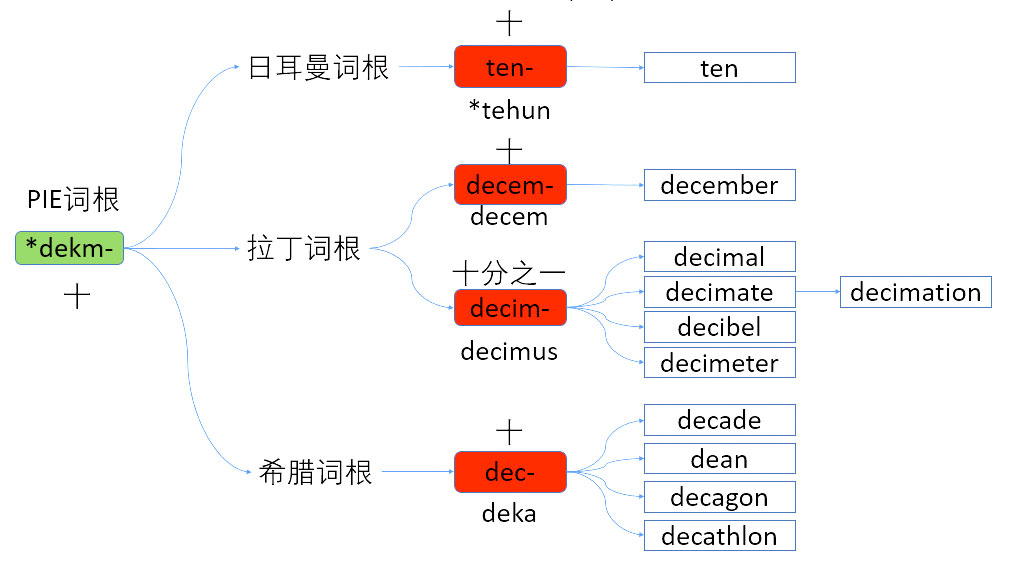
• *dekm-
  • ten 日耳曼
  • deci- 拉丁
  • dec- 希腊

• hexa-
  • six
• hexadecimal
  • sixteen
• 词根清楚了
  • 我们再来明确函数

进制与函数

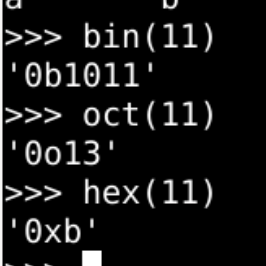
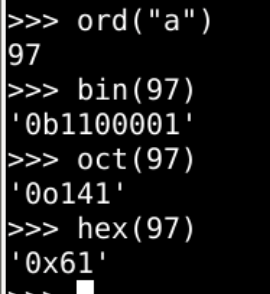
函数名	对应单词	进制类型	数字事例	前缀
bin()	binary	2	0b1100001	0b
oct()	octal	8	0o141	0o
hex()	hexadecimal	16	0x61	0x
?	decimal	10	97	无

• ascii 转化
  • ord(“a”)
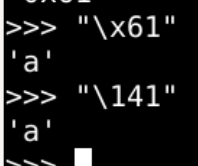
  • chr(65)
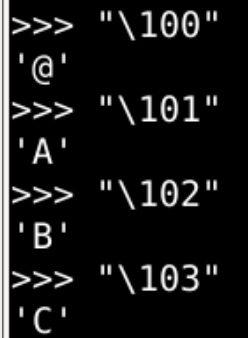
  • \x41 16进制 表示字符A
  • \101 8进制 表示字符A

总结

• 这次总结了四种进制
• 十进制数
  • 可以转化 为
    • 其他进制 的 字符串状态
• 那反过来
  • 其他进制形态的字符串
  • 可以转化回 10进制吗?
• 我们下次再说！
• 蓝桥->https://www.lanqiao.cn/courses/3584
• github->https://github.com/overmind1980/oeasy-python-tutorial
• gitee->https://gitee.com/overmind1980/oeasypython
• 视频->https://www.bilibili.com/video/BV1CU4y1Z7gQ 作者：oeasy