[oeasy]python0083_十进制数如何存入计算机_八卦纪事_BCD编码_Binary_Coded_Decimal

编码进化

回忆上次内容

• 上次 研究了 视频终端的 演化
  • 从VT05 到 VT100
  • 从 黑底绿字 到 RGB 24位真彩色
  • 形成了 VT100选项
• 从而 将颜色 数字化 了

• 生活中我们更常用 10个数字
  • 但是 计算机中 用二进制
• 日常计数的十进制数
  • 是如何存储进计算机的呢?

从10进制到2进制

• 日常生活中 为什么用10进制？
  • 是因为 人的生理结构

• 计算机中 使用2进制
  • 是因为 计算机的生理结构
    • 电灯、开关等电器 有两种状态
• 先回顾一下 之前编码的 历史

编码

• 编码是 绞丝旁的
  • 可以追溯 到有 文字之前

• 结绳 为约
  • 事大 大结其绳
  • 事小 小结其绳
• 上古 结绳而治
  • 后世圣人 易之以书契

八卦

• 事 都往绳子上 系
  • 记住数字 到底是几
• 在绳子上 系住了
  • 这事情就算是 记住了
  • 留下了 纪录

• 以后把绳子 挂出来
  • 进行 比较、判断
  • 这就是 卦
• 经典的卦
  • 三个 位置
  • 可以表示 八种状态
• 事情
  • 都在这八种模式下
  • 普遍联系
  • 千变万化
  • 这就是八卦
• 现代数字 如何编码 呢？

编码格式 演化

• 最早电报时代
  • 数字编码 是 摩斯电码

• 右下角
  • 是数字的 编码
• 长短空
  • 全靠发报人
    • 掌握节奏
    • 控制波特率
• 每个人 都是
  • 自己人工 编码解码
• 然后进入到
  • 电传打字机时代

博多码

• 电传打字机 编码

  • 只有两种状态
    • 0
    • 1
  • 有控制字符
    • Letter
    • Figure

• Figure 包含数字

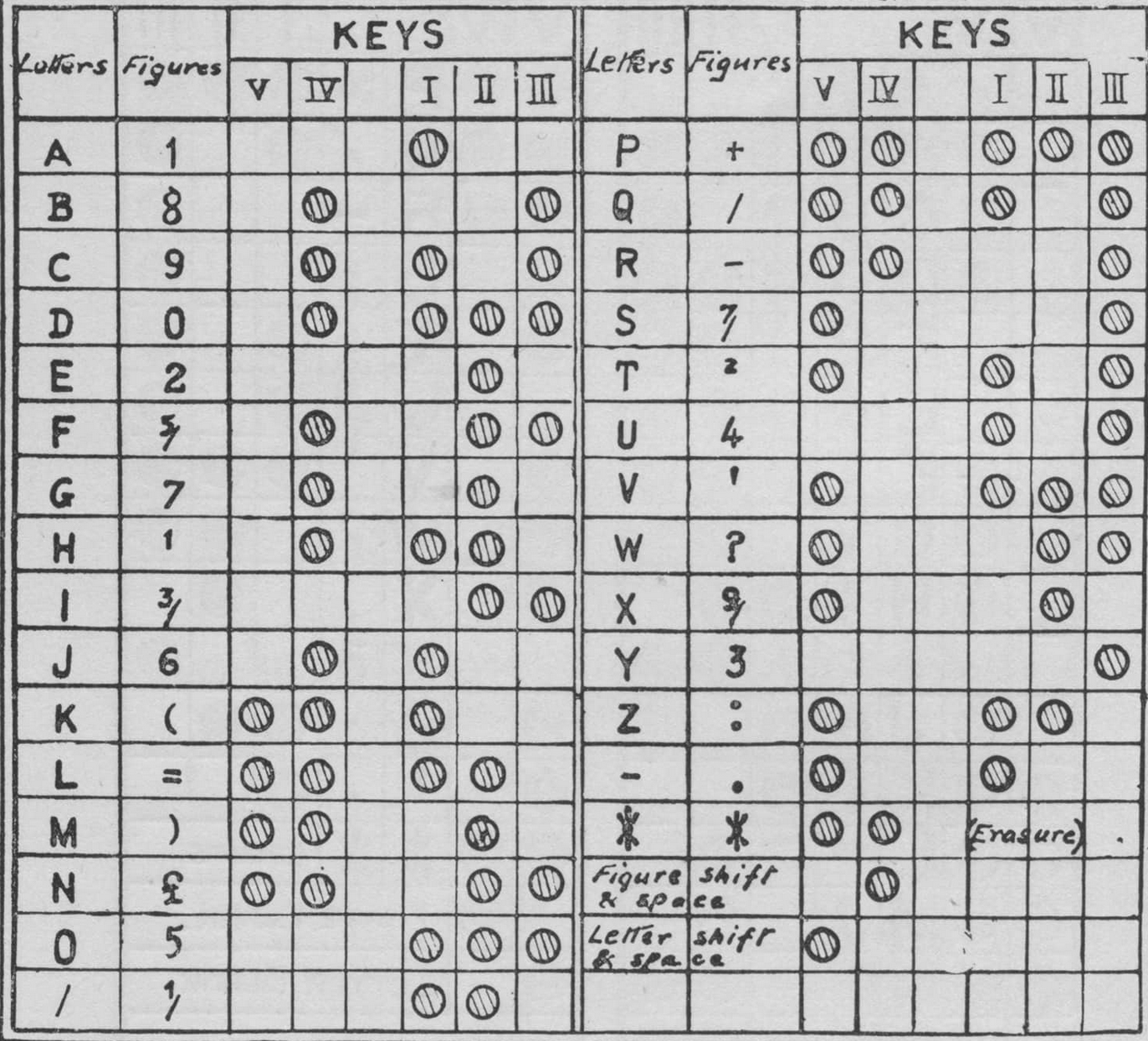
• 这些编码
  • 可以 存储在 纸带上
  • 只有大写 没有小写
  • 符号 不是很丰富
  • 是一种 5-bit 的编码

ibm 的企图心

• 1790s 末
  • ibm 的前身
  • 拿到了 美国人口统计局的 巨大订单
• 在此之前
  • 无论是身份、存款、地产靠的都是纸质的契约
  • 计算机刚刚起步
  • 更没有相互联通的数据中心了

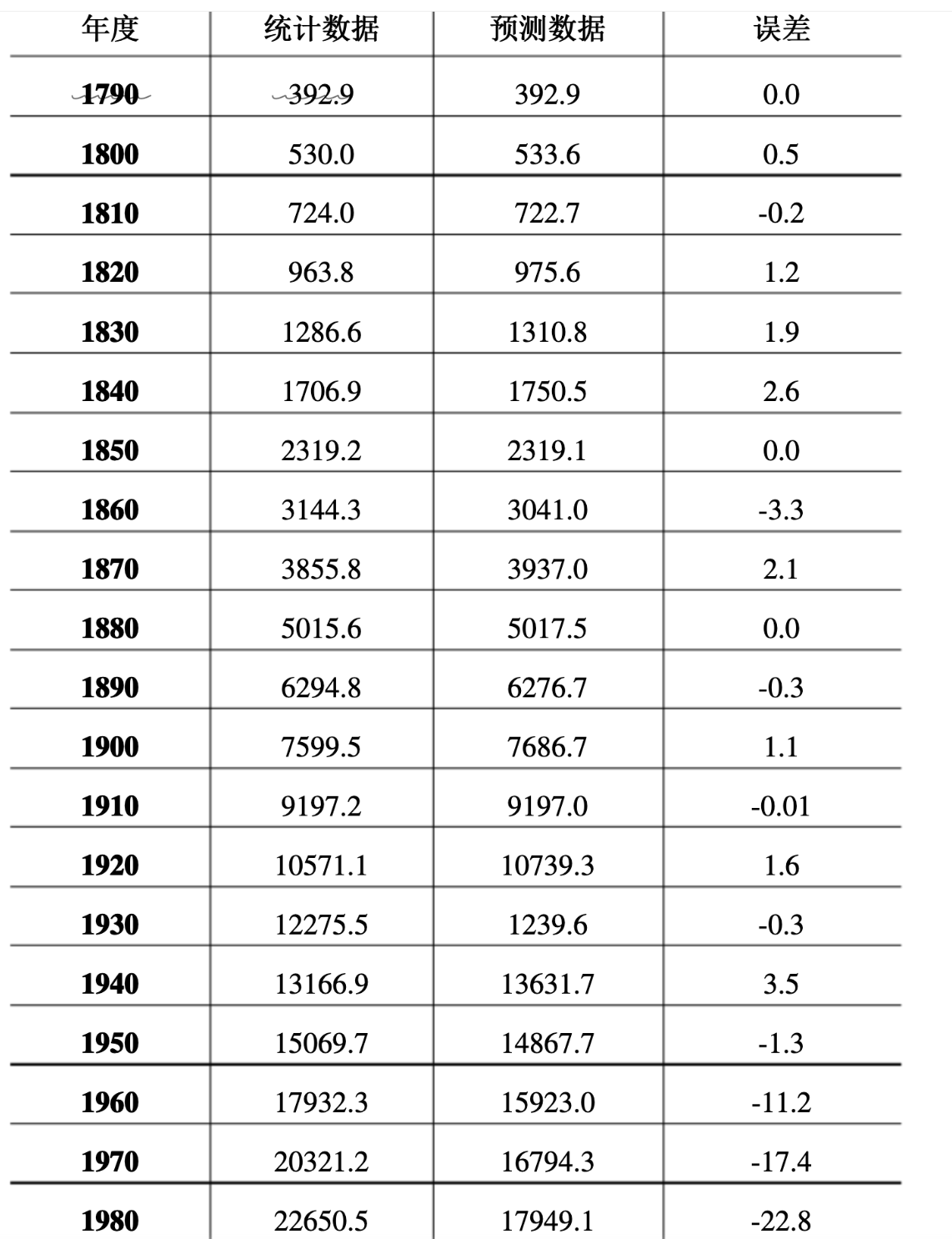
• ibm想要用计算机进行统计
  • 当时用的是 采集卡片
  • 就是去 挨家挨户的 问人家
  • 然后 打卡片打孔
• 在当年
  • 上门查户口 是很明显的冒犯

年龄

• 这统计里面涉及到 统计计数
  • 有数字
  • 就可以对 性别、年龄、地区 分类汇总
  • 而且要 显示出来

• 这纸带上 有很多位置
  • 要么是 打了孔
  • 要么是 没打孔

二进制

• 打孔卡 本质上是
  • 一种二进制的 存储方式

• 通过探针 访问这些打卡孔
  • 可以得到 当前位置上 二进制的值
• 想要表示 10个数字字符的 话？
  • 要使用 多少位 2进制数 呢?

编码十个数目字

• 想要把 10个数字 都编码
  • 3位 2进制数 不够
  • 至少 4位 2进制数

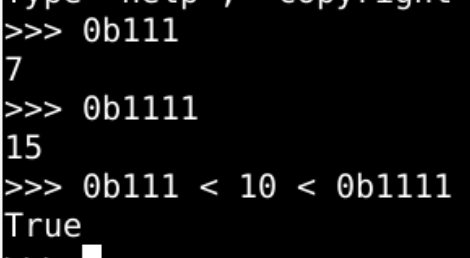
• 就算有了 4位二进制数
  • 究竟如何 编码 呢？

标准 纷争

• 同样是表示 10个数字
  • 有不同的 编码方式

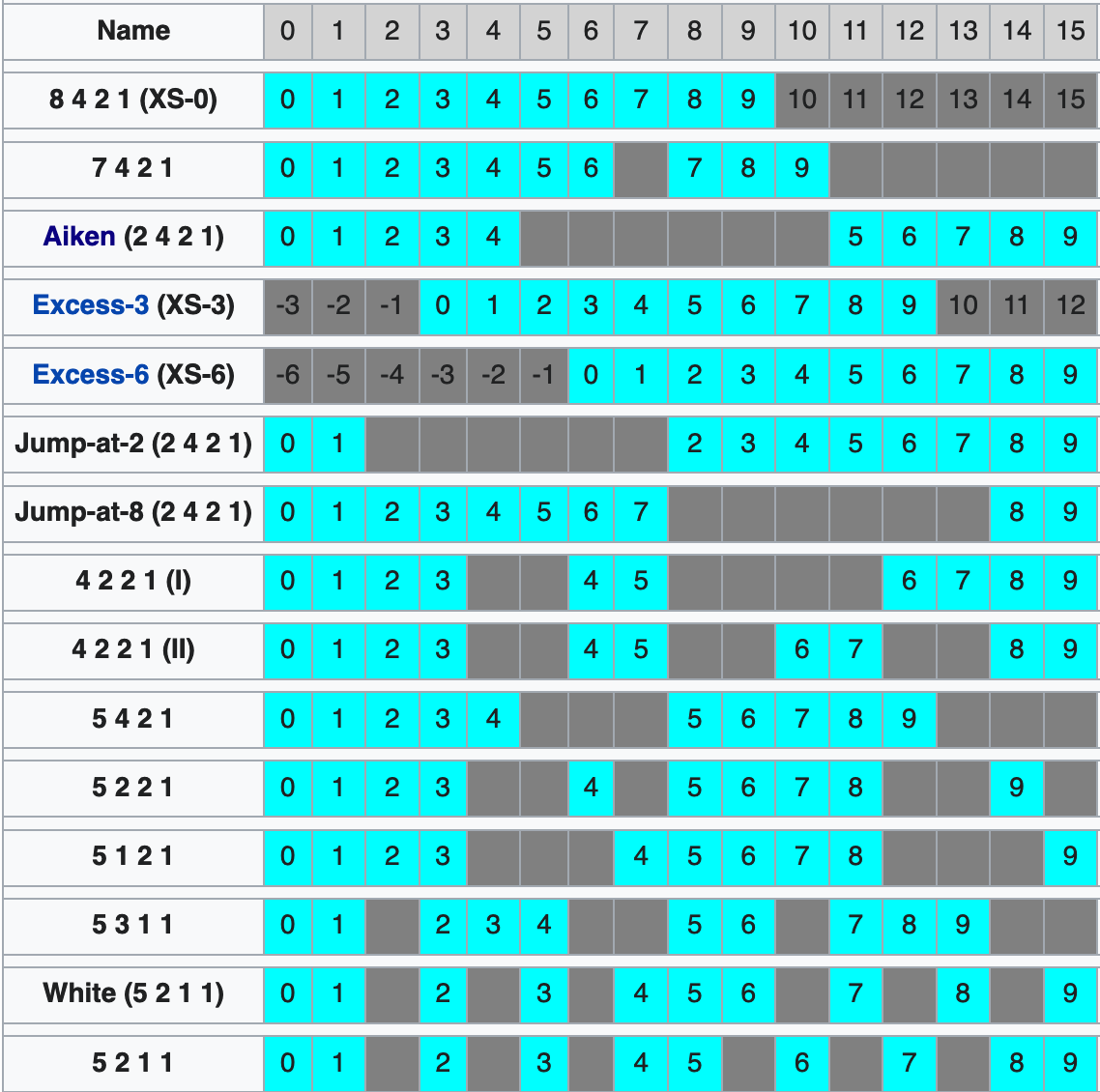
• 不同编码 表示的范围 也不一样
  • 有的是 为了表示的数字 更多
  • 有的是 为了可以表示负数
  • 还有的是 为了加密
• 各种编码之间转化 也需要成本
  • 为了数据 交换方便
  • 编码 还是得 统一
• 到底统一到 什么编码方式 呢？

BCD码

• 最终 统一的编码
  • BCD码
  • Binary Coded Decimal
  • 8421码

• 这个其实比较好理解

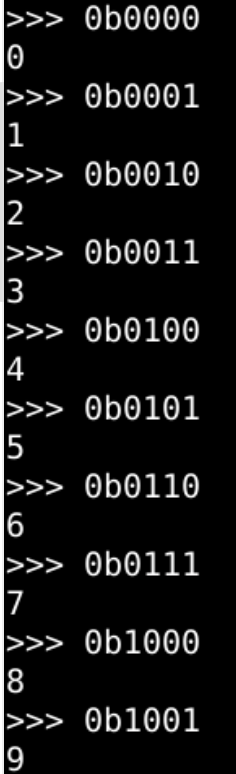
• 使用的是 十进制数字
  • 对应的 二进制数 形态
• BCD码 就叫 8421码
  • 四位 分别代表 8、4、2、1

8421码

• 最终数字领域的 编码统一到
  • BCD码
  • Binary-Coded Decimal
  • 也叫8421码
• 用最简单的 编码方式实现了 统一
  • 8421 点明了 每位二进制数
    • 对应的数值

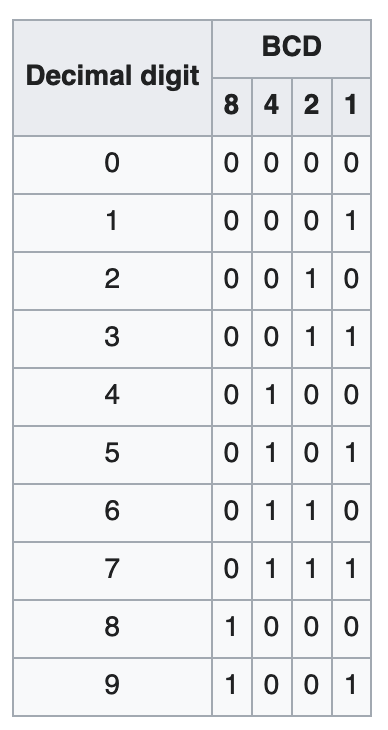
• 这种 编码
  • 其实 就是
    • 纯纯的2进制数形态

数字表示

• 下图中HMS的个位数字 就是 8421编码
  • 从上到下 总共4个二进制位
  • 分别代表8421
  • 竖着一溜 就是一个数字

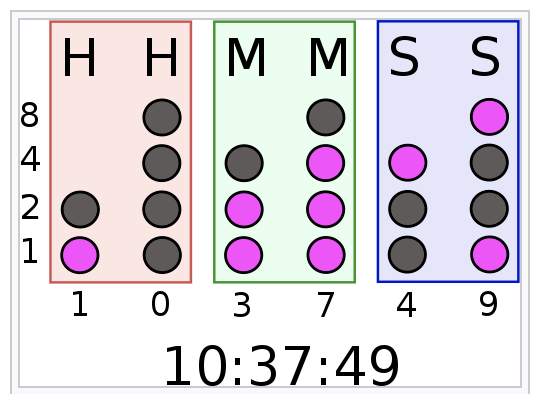
• 小时H 总共两位

  • H十位
    • 最大的小时数 为24
    • 十位数值 不会超过2
    • 所以 两位就够
      • 两位二进制数可 以表示0-3
    • 数值为(0)×2⁰+(1)×2⁰ = 1
  • H个位
    • 最大的数字就是9
    • 不会超过10
    • 总共需要4位
    • 数值为(0)×2⁰+(0)×2⁰ = 0
  • 小时的 总体数值为10

• 分钟和秒钟

  • 逻辑类似

• 根据 这个编码

  • 就可以 输出到
    • 当时的 输出设备

辉光钟

• 辉光钟 是一种较为原始的 输出设备

  • 输出的结果 是10进制数字形态
  • 毕竟作为人类 读二进制数字 比较费劲

• 12根管脚

  • 数字是几
  • 几就亮

• 后来有了led之后
  • 出现了 seg-7
  • 七位数码管

七位数码管

• 计算机内部
  • 得到具体二进制数字

• 然后根据二进制数字
  • 得到数码管的led状态

• 字型是如何生成的呢？

led编码

• 七位数码管
  • 有7个led灯

• 将每个灯
  • 进行编码

BCD码在今天

• 在今天的 ascii 中
  • 数字字符对应的字节
    • 是0x30-0x39

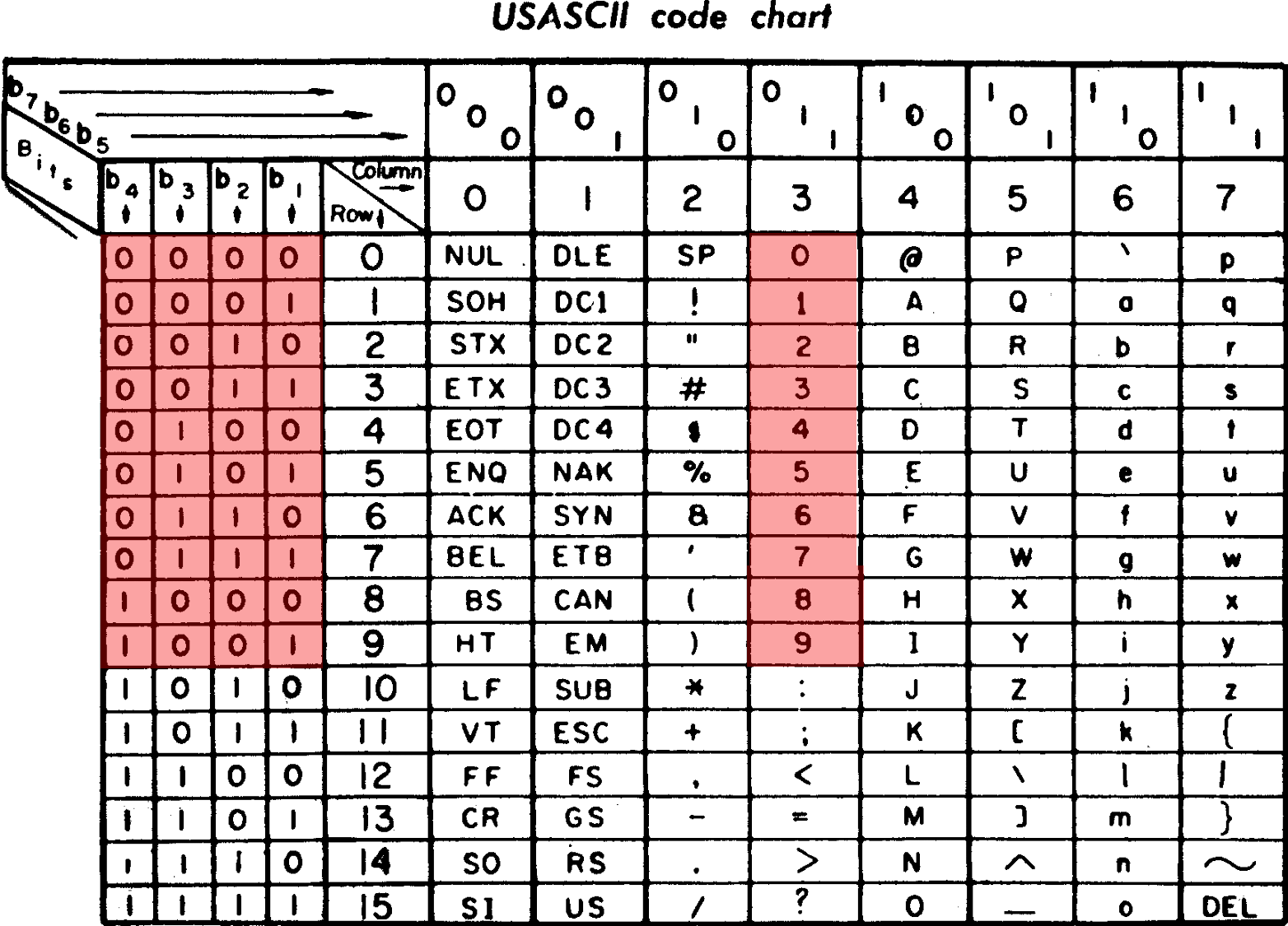
• 0x30-0x39 的 后4位 也还是 BCD编码
• 10进制数字
  • 就是这样编码
    • 进入 二进制的计算机世界
• 那么
  • 字母又是 怎么进入数字世界的 呢？
• 先去总结一下BCD

总结

• 这次 回顾了
  • 数字 进入二进制世界的 过程
• 采用的编码是BCD
  • Binary Coded Decimal
    • 也叫8421码
    • 十进制数的 二进制形态
• 数字的 输出形式
  • 辉光管
  • 数码管

• 除了数字 之外

  • 还有 字母

• 字母 是如何编码进入计算机世界的 呢？

• 我们下次再说！

• 蓝桥->https://www.lanqiao.cn/courses/3584

• github->https://github.com/overmind1980/oeasy-python-tutorial

• gitee->https://gitee.com/overmind1980/oeasypython

• 视频->https://www.bilibili.com/video/BV1CU4y1Z7gQ 作者：oeasy