【目标检测】二、Fast R-CNN与SVD

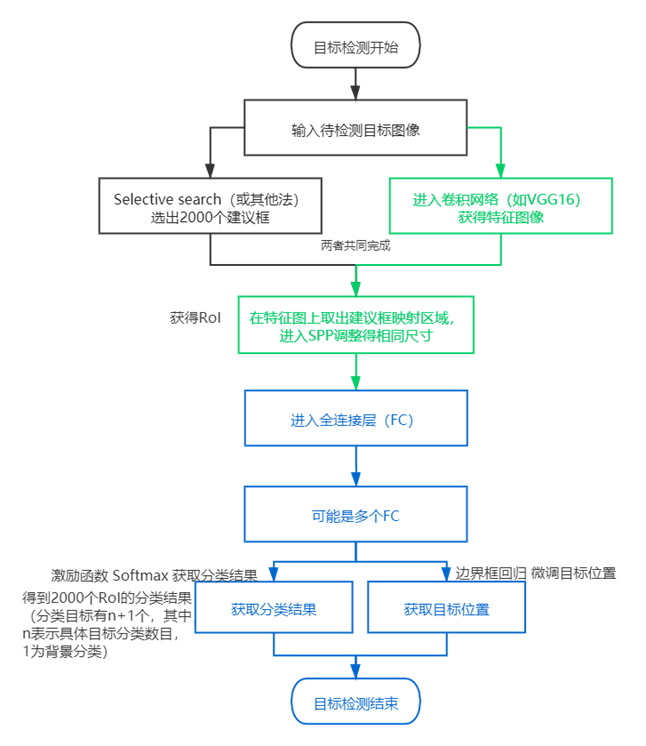
1.流程

（1） 空间金字塔池化（spatial pyramid pooling，SPP）

原理：

（2）Fast-RCNN

2.数学概念

这么多个全连接层，必然存在计算的性能问题，让数学家们蠢蠢欲动——基于奇异值分解（singular value decomposition，SVD）的全连接层计算加速方法。

降维（dimensionality reduction）处理主要方式：

主成分分析 Principal Component Analysis，PCA	下文补充
因子分析 Factor Analysis	假设观察的数据当中存在一个隐变量（latent variable），这些数据是由隐变量和噪声的线性组合而成，如果能找到隐变量，就可以减少观察数据当中噪声而达到降维效果。
独立成分分析 Independent Component Analysis，ICA	假设一批数据是由多个数据源混合在一起的，这些数据源应该是相互独立，没有关系，若能找到有几批数据源就可以达到降维效果。

（1）PCA

（以下若有误请指正）

解n元一次的方程，得到基础解系是“基”，所有通解都可以用基础解系的向量线性表出。

假设解线性方程（n个特征列）中，初等变换后得到化简系数的矩阵，得到了矩阵的秩r，那么n-r得到n个变量中r个受到约束后剩下的n-r个自由变量。

可以这样理解，基础解系是基，由向量组成（是约束下的解的坐标系）

求得的自由变量就是这个基的轴，形如(1,0,0)，(0,1,0)这样表示的三维坐标轴一样，设第一个轴是(1,0,…,0)，第一个轴是(0,1,…,0)，第n个轴是(0,0,…,1)，得到了这些轴在m维坐标系中的方向（m=r）。每一个自由变量是基的一条轴。

如果能求到特征值和特征向量，再通过形如Av=λv的高维到低维映射，就能达到降维效果，即：矩阵A的数据在特征向量基中的表示。

其中，特征值个数=矩阵的秩，一个特征值带着一个特征向量。

这个思路下，PCA可以这样下手：

找到一个基空间（其轴的数目取数据特征列数），确定从原数据的行数据映射（点乘）到基空间的数值，这个数值就是降维结果。

而怎么确定基空间（轴的方向、长度是什么），

从几何上看，是希望找到一条线，它覆盖最大差异的数据，然后再找覆盖次大差异数据的线，以此类推。

方差公式σ（Sigma，大写Σ，小写σ）：

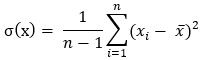
拓展至协方差公式，从某种程度来说，方差也是x的协方差：

协方差矩阵Σ [2]，是对称矩阵：

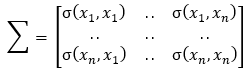
PCA实现 [3]：

from numpy import *
def pca(dataMat, topNfeat = 999): 　　　　　　　　　　　　　　# shape (m, n), (t)
    meanVals = mean(dataMat, axis=0) 　　　　　　　　　　　　# 求得平均值
    # 求新空间向量（特征向量）
    meanRemoved = dataMat - meanVals
    covMat = cov(meanRemoved, rowvar=0)　　　　　　　　　　  # 求协方差矩阵
    eigVals, eigVects = linalg.eig(mat(covMat))　　　　　  # 求协方差矩阵的特征值及特征向量，shape (1, n) , (n, n)
    eigValInd = argsort(eigVals) 　　　　　　　　 　　　　　 # 特征值排序，shape (1, n)
    eigValInd = eigValInd[:-(topNfeat+1):-1]　　　　　　　 # 取特征值最大的前N个，shape (1, t)
    redEigVects = eigVects[:,eigValInd] 　　　　　　　　　　# 特征值对应的特征向量，shape (n, t)
    # 将数据转换到新空间
    lowDDataMat = meanRemoved @ redEigVects 　　　　　　　　# 到低维的映射，其中@是点乘运算符， shape (m,n) (n,t) -> (m,t)
    reconMat = (lowDDataMat @ redEigVects.T) + meanVals  # 数据还原 shape (m, t) (t, n) -> (m, n)
    return lowDDataMat, reconMat

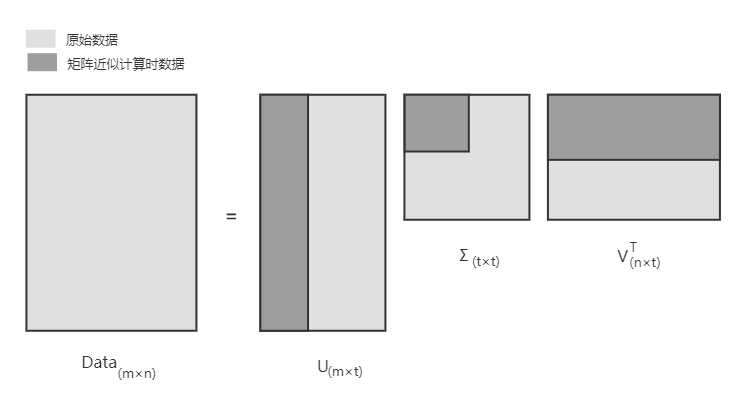
（2）奇异值分解（Singular Value Decomposition，SVD）

在大量数据下的PCA计算代价是很大的，这个时候常用SVD做矩阵分解以减少计算量。

SVD是常用的降维手段，它可以通过隐性语义索引（Latent Semantic Indexing，LSI，或者隐性语义分析Latent Semantic Analysis，LSA）应用到搜索和信息检索、推荐引擎等。（它希望在搜索一个词时，能把同义词映射为同一概念）

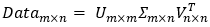
Σ(sigma)是一个矩阵，只有对角元素，其它元素为0。它的值就是原数据矩阵Data的奇异值，取Data的特征值开方 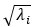，并且按从大到小的排序。

实现的类库：

import numpy as np
U, Sigma, Vt = np.linalg.svd(np.array([[1,1],[7,7]]))
U,Sigma,Vt

>>> (array([[-0.14142136, -0.98994949],
        [-0.98994949,  0.14142136]]),
 array([10.,  0.]),
 array([[-0.70710678, -0.70710678],
        [-0.70710678,  0.70710678]]))

注，在大矩阵计算中，计算结果会有些许偏差，这和计算的具体实现相关，但数量级上是不变的，也即：

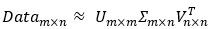
作矩阵分解的话，可以尝试还原矩阵，当然这是在小数据上的测试，证明一下分解的可行性，以及导致误差的可能：

import numpy as np
data = np.array([
    [1,1,1,0,0],
    [2,2,2,0,0],
    [5,5,5,0,0],
    [1,1,0,2,2],
    [0,0,0,3,3],
    [1,1,1,0,0],
    [0,0,0,1,1]
])
U, Sigma, Vt = np.linalg.svd(data)
#print('sigma:', Sigma)
sig3 = [[Sigma[0],0,0],[0,Sigma[1],0],[0,0,Sigma[2]]]
sig3 = np.array(sig3)
U[:,:3]@Sig3@Vt[:3,:] # 多个矩阵点乘，除了numpy.linalg.multi_dot和reduce的写法，numpy（在python 3.5以后）重载了@运算符，A@B直接就是A和B的矩阵乘法。

>>>array([[ 1.00000000e+00,  1.00000000e+00,  1.00000000e+00,  -2.85152832e-16, -2.94802231e-16],
  [ 2.00000000e+00,  2.00000000e+00,  2.00000000e+00,  -1.48291534e-16, -1.67590333e-16],
  [ 5.00000000e+00,  5.00000000e+00,  5.00000000e+00,   1.05859966e-16,  5.77213899e-17],
  [ 1.00000000e+00,  1.00000000e+00, -1.05947783e-15,   2.00000000e+00,  2.00000000e+00],
  [ 1.73854477e-16,  4.09482862e-16, -8.23917306e-16,   3.00000000e+00,  3.00000000e+00],
  [ 1.00000000e+00,  1.00000000e+00,  1.00000000e+00,  -6.80558595e-17, -7.77052588e-17],
  [ 4.44607724e-17,  1.29942461e-16, -2.79696374e-16,   1.00000000e+00,  1.00000000e+00]])

还原当中的Σ只取了3项，这个3如何确定？

一种方式：求得所有奇异值的平方和*0.9作为阈值，再逐个计算奇异值平方和累加到阈值数目为止，以此来确定矩阵Σ的大小；

另一种方式：直接由数据情况来确定，比如说直接指定2000或3000。

SVD的图像压缩示例：

def imgCompress(numSV=3, thresh=0.8):
    myl = []
    for line in open('0_5.txt').readlines():
        newRow = []
        for i in range(32):
            newRow.append(int(line[i]))
        myl.append(newRow)
    myMat = mat(myl)
    print "****original matrix******"
    printMat(myMat, thresh)
    U,Sigma,VT = la.svd(myMat)
    SigRecon = mat(zeros((numSV, numSV)))

    for k in range(numSV):#construct diagonal matrix from vector
        SigRecon[k,k] = Sigma[k]

    reconMat = U[:,:numSV]@SigRecon@VT[:numSV,:]

    print "****reconstructed matrix using %d singular values******" % numSV
    printMat(reconMat, thresh)

imgTest.txt 内容：

00000000000000110000000000000000
00000000000011111100000000000000
00000000000111111110000000000000
00000000001111111111000000000000
00000000111111111111100000000000
00000001111111111111110000000000
00000000111111111111111000000000
00000000111111100001111100000000
00000001111111000001111100000000
00000011111100000000111100000000
00000011111100000000111110000000
00000011111100000000011110000000
00000011111100000000011110000000
00000001111110000000001111000000
00000011111110000000001111000000
00000011111100000000001111000000
00000001111100000000001111000000
00000011111100000000001111000000
00000001111100000000001111000000
00000001111100000000011111000000
00000000111110000000001111100000
00000000111110000000001111100000
00000000111110000000001111100000
00000000111110000000011111000000
00000000111110000000111111000000
00000000111111000001111110000000
00000000011111111111111110000000
00000000001111111111111110000000
00000000001111111111111110000000
00000000000111111111111000000000
00000000000011111111110000000000
00000000000000111111000000000000

关于SVD的推理/原理，暂且搁置。

线性代数有感：

它真的有很多性质，最后接触已经近乎三年前了，也都忘了，不过遇到也不怕吧，它花里胡哨总归是为了线性计算；它恁多的性质都是为了计算方便，

此处我只追求，我能get到其型，具体计算就不深入。

=======================================================================

资料：

[2] 协方差相关 https://zhuanlan.zhihu.com/p/37609917

[3]Peter Harrington著《机器学习实战》

杜鹏、谌(chen2)明、苏统华 编著《深度学习与目标检测》