CF1988D The Omnipotent Monster Killer

CF1988D The Omnipotent Monster Killer

本文同步于我的网站。

Problem

怪物们在一棵有 \(n\) 个顶点的树上，编号为 \(i(1\le i\le n)\) 的怪物位于编号为 \(i\) 的顶点上，攻击力为 \(a_i\) 。你需要与怪物战斗 \(10^{100}\) 个回合。在每个回合中，会依次发生以下两步：

1. 所有活着的怪物攻击你。你的生命值会按照所有活体怪物攻击点的总和减少。
2. 您选择一些（可以选全部，也可以不选）怪物并杀死它们。被杀死的怪物将不会再进行攻击。

限制条件：在一个回合内不能杀死相邻的两只怪物。

如果您以最佳选择方式攻击的怪物，那么在所有回合后，您的健康值减少的最小值是多少？

\(1\le t\le 10^4,1\le n\le 3\cdot 10^5,1\le a_i \le 10^{12},\sum n\le 3\cdot 10^5\)

Solution

这是一道再经典不过的树形DP了。太惭愧了。

每个节点的贡献可以表示为 \(w_i\cdot a_i\) 的形式，其中 \(w_i\) 表示怪物 \(i\) 是第 \(w_i\) 次被杀死的。可以证明 \(w_i\) 不会超过 \(\log_2(n)\) 。

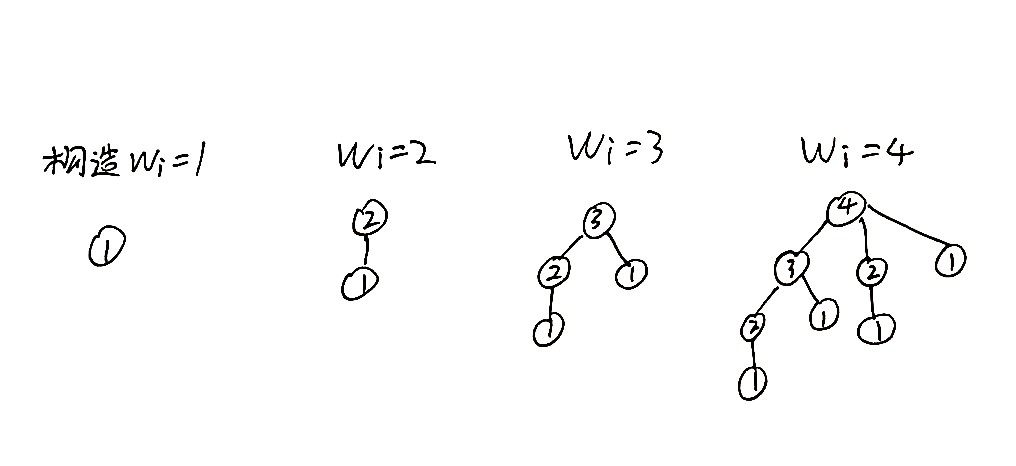
图：Taibo

上图中，欲构造出 \(w_i=x\) 的点，需要将该点连接上 \(w=1,2,\dots,x-1\) 的节点。设构造出 \(\max w_i=n\) 的树至少需要 \(tot_n\)​ 个节点，则存在

\[\begin{gather}
tot_n=
\begin{cases}
& 1 & n=1\\
& \sum_{i=1}^{n-1}tot_i +1 & n\ge 2
\end{cases}
\end{gather}
\]

即得 \(tot_n=2^n\) 。也就是说对于一张 \(n\) 个节点的图，其至多需要 \(\log_2(n)\) 次选择就可以将所有怪物杀死。

下面开始dp。设 \(dp_{x,k}\) 表示若第 \(k\) 次杀死怪物 \(x\) ， \(x\) 子树内的怪物至少会产生多少点伤害。

\(dp_{x,k}\) 由两部分组成：

• 在第 \(k\) 次杀死怪物 \(x\) 之前，怪物 \(x\) 会产生 \(k\cdot a_x\) 点伤害。
• \(x\) 的子树内的怪物（除了 \(x\) 本身）产生的伤害。

\[\begin{gather}
dp_{x,k}=k\cdot a_x + \sum_{y\in u(x)}\min_{j\not =k} dp_{y,j}
\end{gather}
\]

其中 \(u(x)\) 表示点 \(x\)​ 的儿子节点。

最后答案为 \(\min dp_{root,k}\)

Code

#define N 300010

int n;
int head[N],nxt[N*2],ver[N*2],cnt;
void insert(int x,int y)
{
	nxt[++cnt]=head[x];
	head[x]=cnt;
	ver[cnt]=y;
}

LL a[N];

#define K 25
#define inf (1ll<<62)
LL dp[N][K+5];

void dfs(int x,int f)
{
	for(int i=1;i<=K;i++)
	{
		dp[x][i]=a[x]*i;
	}

	for(int i=head[x];i;i=nxt[i])
	{
		int y=ver[i];
		if(y==f) continue;
		dfs(y,x);
		for(int j=1;j<=K;j++)//点x将被第j次选
		{
			LL mn=inf;
			for(int k=1;k<=K;k++)//相邻点y将被第k次选
			{
				if(j!=k)
				{
					mn=min(mn,dp[y][k]);
				}
			}
			dp[x][j]+=mn;
		}
	}
}

int main()
{
	ios::sync_with_stdio(false);
	cin.tie(0);
	cout.tie(0);
	cout.precision(10);
	int t=1;
	cin>>t;
	while(t--)
	{
		cin>>n;
		for(int i=1;i<=n;i++)
		{
			cin>>a[i];
		}
		for(int i=1;i<n;i++)
		{
			int x,y;cin>>x>>y;
			insert(x,y);
			insert(y,x);
		}

		dfs(1,0);

		LL ans=inf;
		for(int i=1;i<=K;i++)
		{
			ans=min(ans,dp[1][i]);
		}

		cout<<ans<<endl;

		for(int i=1;i<=cnt;i++)
		{
			head[i]=nxt[i]=ver[i]=0;
		}
		cnt=0;
	}
	return 0;
}