ed25519加密签名算法及应用

刷知乎时看到一篇文章，很感兴趣，来学习一下！

转载文章：ed25519加密签名算法及应用

初次使用Github时都需上传本地的公钥，这时需要提前在本地生成密钥对，使用的是ssh-keygen命令：

ssh-keygen -C "your_email@example.com"

该命令属于OpenSSH，win10系统自带，linux一般也自带，且支持多种加密签名算法，其中也支持ed25519：

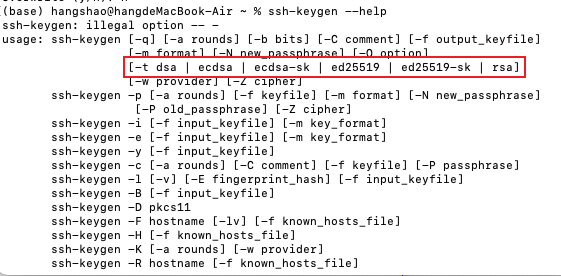
介绍

ed25519是一种EdDSA签名，基于SHA-512和Curve25519，可以看出他的命名取自EdDSA和Curve25519的前半和后半。

EdDSA(Edwards-curve Digital Signature Algorithm)是基于扭曲爱德华兹曲线(twisted Edwards curves)的一类签名算法，
Curve25519是扭曲爱德华兹曲线的一种。

爱德华兹

爱德华兹(Harold Edwards)是美国数学家，从事数论、代数以及数学历史和哲学工作，1936-2020，享年84岁。

爱德华兹20岁毕业于威斯康星大学麦迪逊分校
21岁获得哥伦比亚大学文学硕士学位
25岁获得哈佛大学博士学位
曾在哈佛大学和哥伦比亚大学任教，30岁加入纽约大学，66岁成为名誉教授，76岁成为美国数学学会成员。

看看大佬‍♂️的经历，膜拜～

主要著作有高级微积分、黎曼函数、费马最后定理等书籍。

前NBC新闻记者、作家罗琳(Betty Rollin)是爱德华兹的妻子，和小野洋子(Ono Yoko)是同学，而小野洋子是披头士乐队列侬(John Lennon)的妻子。

附上来自纽约大学的介绍：https://www.math.nyu.edu/faculty/edwardsd/

椭圆曲线

形如$y^2=x^3+ax+b$ 的曲线，关于更多椭圆曲线的介绍参考：

1、https://zhuanlan.zhihu.com/p/35618744

2、https://www.cnblogs.com/pam-sh/p/16564541.html

爱德华曲线

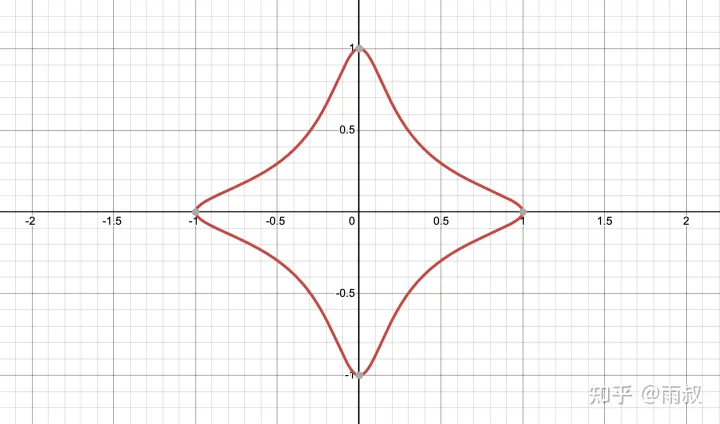
爱德华兹曲线，d=-30

形如$x^2+y^2=1+dx^2y^2$ 的曲线，可以称为爱德华兹曲线，被爱德华兹于2007年研究发表，二元二次曲线，看起来非常工整。

扭曲爱德华兹曲线

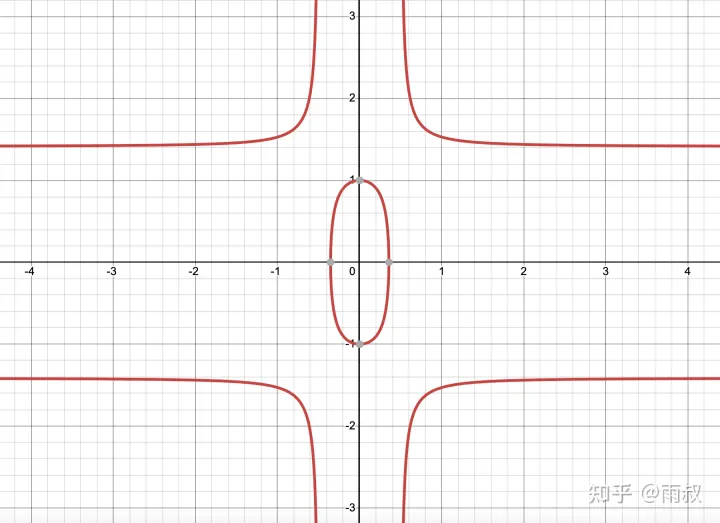
扭曲爱德华兹曲线，a=8，d=4

形如 $ax^2+y^2=1+dx^2y^2$ 的曲线，可以称为扭曲爱德华兹曲线，其中$a,d≠0,a≠d$。字如其名，多了常数 a ，可以理解为加入这个常数 a 后曲线相应地变形了。

蒙哥马利曲线

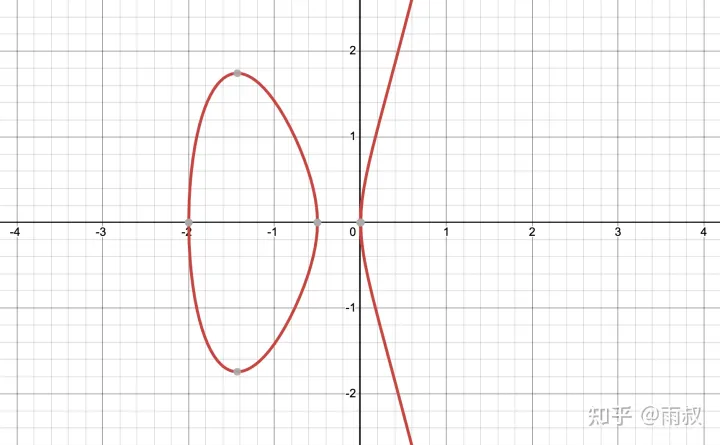
蒙哥马利曲线，B=0.25，A=2.5

形如 $By^2=x^3+Ax^2+x$ 的曲线。看到这里，我相信当年椭圆曲线对数学家来说无疑是新大陆，加个常数，研究一下特性，就可以用自己的名字命名了。【～】

Curve25519

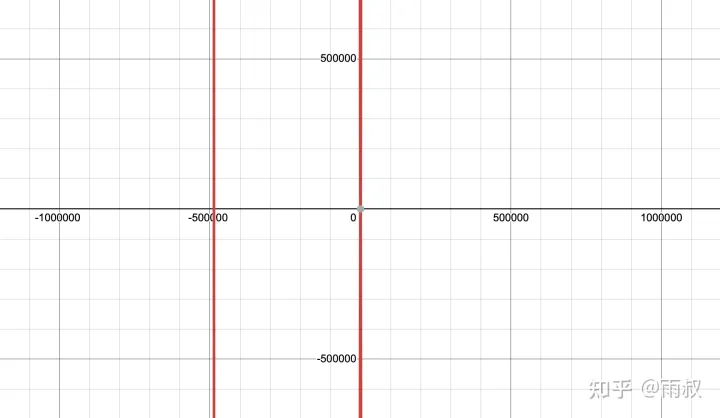
蒙哥马利曲线，B=1，A=486662

$y^{2}=x^{3}+486662 x^{2}+x$，图像很不直观了，是蒙哥马利曲线的实例，其中 $p=2^{255}−19$ ，因此命名为曲线25519，2005年被伯恩斯坦发表。

ed25519曲线

$-x^{2}+y^{2}=1-\frac{121665}{121666} x^{2} y^{2}$，是扭曲爱德华兹曲线的实例，和Curve25519可以相互转化。

25519系列曲线自2005年发表以来，除了学术界无人问津。2013年斯诺登曝光棱镜计划后，人们发现美国安全局有可能实现基于P-256曲线的Dual_EC_DRBG算法后门，并怀疑P曲线的常数是特意选出的，方便美国安全局破解该算法。此后，25519曲线代替P-256曲线被广泛应用，OpenSSH迅速增加了对25519系列的支持。

EdDSA

基于ed25519曲线的EdDSA签名算法的公钥较短，为32个字节。四核2.4GHz的cpu每秒可以签名109000次，哈希碰撞攻击无效。总而言之，ed25519签名算法是一个高速、高安全性的签名算法。

在另外一篇文章也提到：在 Apple 最近发布的iOS 安全白皮书中，讲述在 Apple 生态系统中广泛使用 ECDSA。通过 iMessage 发送的消息使用 ECDSA 进行签名，而 iCloud 钥匙串同步依赖于 ECDSA。越来越多的技术将 ECDSA 用于安全性，包括端到端加密消息服务TextSecure和CryptoCat。

安全性与RSA相当，且密钥更短！

密钥的安全性取决于其大小和算法。有些算法比其他算法更容易破解，并且需要更大的密钥才能获得相同的安全级别，破解 RSA 密钥需要考虑一个很大的数字。随着硬件的进步以及量子计算的出现，我们越来越擅长分解大量数字【大数分解问题】，破解ECDSA密钥需要解决椭圆曲线离散对数问题 (ECDLP)，自从 Koblitz 和 Miller 在 1985 年独立引入以来，数学界在改进算法以解决这个问题方面没有取得任何重大进展。

这意味着使用 ECDSA，可以获得与 RSA 相同级别的安全性，但密钥更小。由于几个原因，较小的键比较大的键更好：较小的密钥具有更快的生成签名的算法，因为数学涉及较小的数字，更小的公钥意味着更小的证书和更少的数据来建立 TLS 连接，这意味着更快的连接和更快的网站加载时间。

使用

java

ECDSA签名算法，封装在JDK中，且只在JDK1.7之后才有

public static void main(String[] args) throws Exception {

    //生成公钥私钥

    KeyPair keyPair1 = getKeyPair();

    PublicKey publicKey1 = keyPair1.getPublic();

    PrivateKey privateKey1 = 				keyPair1.getPrivate();

    //密钥转16进制字符串

    String publicKey = HexUtil.encodeHexString(publicKey1.getEncoded());

    String privateKey = HexUtil.encodeHexString(privateKey1.getEncoded());

    System.out.println("生成公钥："+publicKey);

    System.out.println("生成私钥："+privateKey);

    //16进制字符串转密钥对象

    PrivateKey privateKey2 = getPrivateKey(privateKey);

    PublicKey publicKey2 = getPublicKey(publicKey);

    //加签验签

    String data="message";

    System.out.println("消息："+data);

    String signECDSA = signECDSA(privateKey2, data);

    System.out.println("签名："+signECDSA);

    boolean verifyECDSA = verifyECDSA(publicKey2, signECDSA, data);

    System.out.println("验签结果："+verifyECDSA);

}

使用openSSL库

int main()

{

    generateKey_test();

    sign_test();

    verify_test();

    return 0;

}

程序见github

参考

1、https://en.wikipedia.org/wiki/EdDSA

2、https://datatracker.ietf.org/doc/html/rfc8032

3、https://blog.csdn.net/xujunkai66/article/details/104801346

4、https://blog.csdn.net/qq_41987680/article/details/124888222