Luogu P8710 [蓝桥杯 2020 省 AB1] 网络分析 题解 [ 绿 ] [ 带权并查集 ]

原题

分析

本题由于从一个节点发信息，同一个集合内的所有点都会收到信息，显然是一道要求维护各节点间关系的题，因此采用并查集的数据结构进行求解。

但由于维护关系的同时还要维护权值，所以采用带权并查集，它是一种能维护某个节点与其祖宗节点之间关系的数据结构。

带权并查集找父亲的模板如下：

int findf(int x)
{
	if(f[x]==x)return x;
	int orif=f[x];
	f[x]=findf(f[x]);
	dis[x]+=dis[orif];
	return f[x];
}

正常思路就是合并操作照常做，加上某个值就打上懒标记。

但是本题是否就这样结束了？

并不是，首先可以观察到本题要求的并不是简单的某节点和祖宗的关系，因为祖宗节点在和另一个集合合并之前，他们的储存信息是不互通的，如果仅仅就此进行合并，那么合并时某一个集合的储存信息就会平白无故地加上另一个集合在合并前的储存信息，这是不符合题意的。

而想要解决这个问题，就要将两个集合合并后分开来，即不能让一个集合祖宗的父亲，是另一个集合的祖宗。

因此，就要让他们分居不同的子树中，自然而然地就想到了虚点的解决方法。

细节实现

对于合并操作：

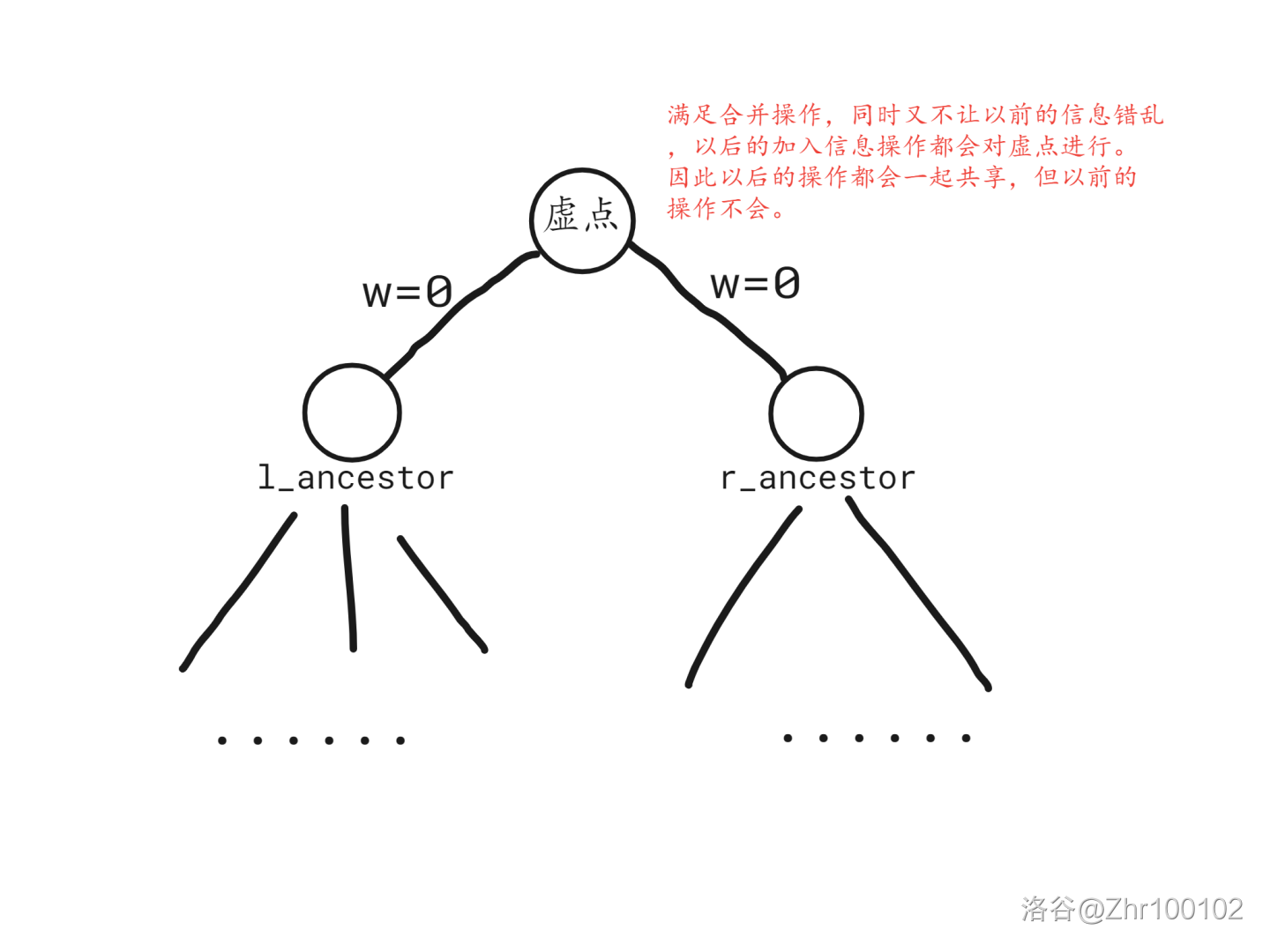
先找到两个集合的祖宗节点，然后创建一个虚点，使其成为这两个祖宗节点的父节点，这样就使两个集合变成了一个集合。

同时需要注意，由于合并后并没有改变两集合内任何一个节点的储存信息，所以从祖宗节点到虚点的边权为 \(0\) 。

对于发送信息操作：

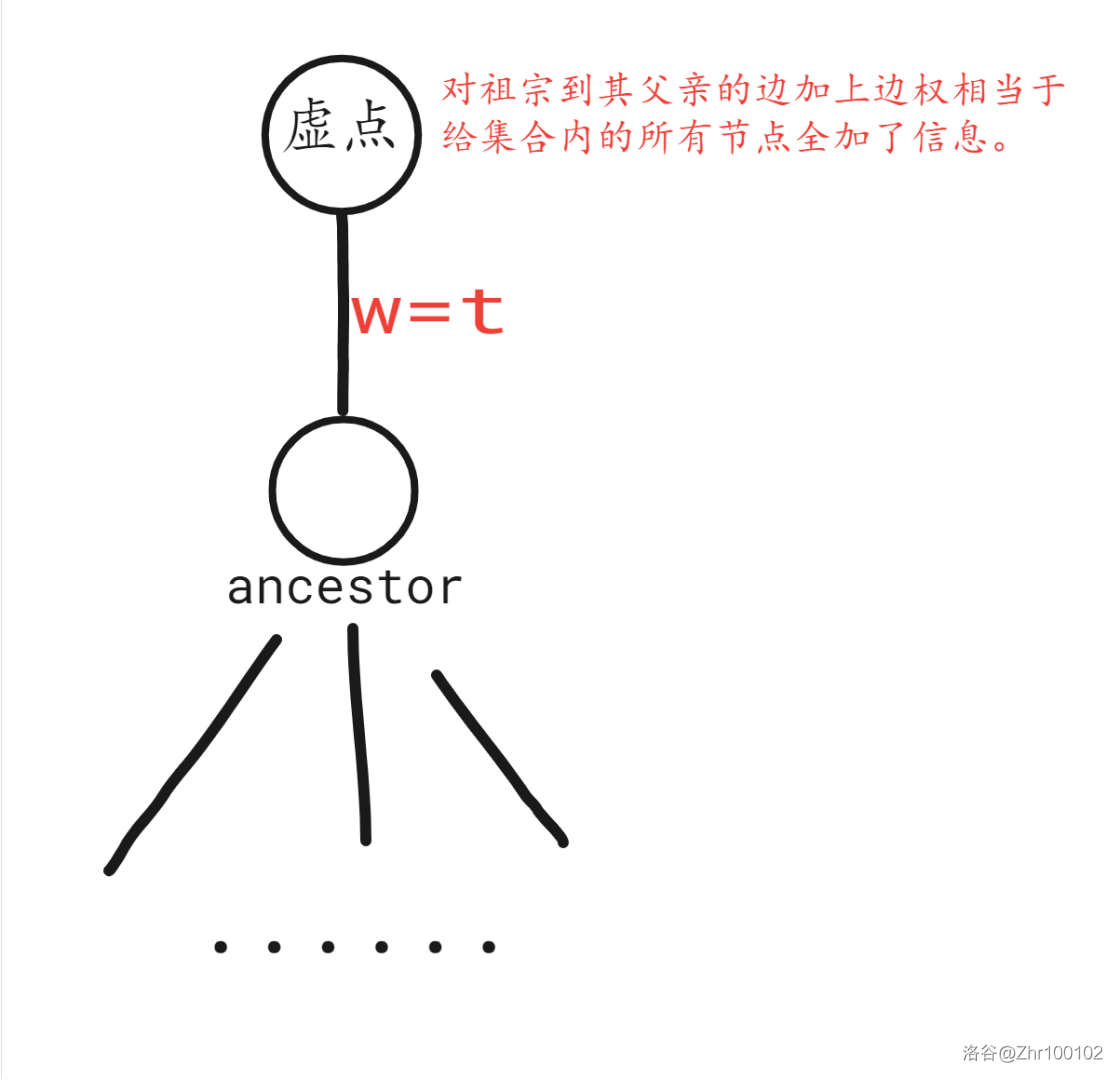
依旧是先找到这个集合的祖宗节点，然后创建一个虚点，把这个虚点作为祖宗节点的父节点。

但边权方面有所不同，这个操作由于要让集合里的所有节点都接收储存信息（包括祖宗节点），因此祖宗节点到虚点的边权为储存信息的大小 \(t\) 。

当然也可以用懒标记实现，但为了使方法统一，这里加上某个值也采用虚点的方式。

输出处理

先更新一遍它到祖宗节点的距离，即它现在存储信息的大小，这样才能保证答案正确。

然后对于每个节点 \(i\) ，输出 \(dis[i]\) 即可。

由于总操作数只有 \(10^5\) ，所以最多只会有 \(10^5\) 个虚点，最坏的情况下并查集有 \(1.1*10^5\) 个节点，时间和空间复杂度都正确。

代码

#include <bits/stdc++.h>
using namespace std;
int n,m,t,f[200005],dis[200005],cnt=20000,opt,a,b;//cnt为当前要添加的虚点的编号
void init()//初始化
{
	for(int i=1;i<=200000;i++)
	{
		f[i]=i;
		dis[i]=0;
	}
}
int findf(int x)//找父节点+更新距离
{
	if(f[x]==x)return x;
	int orif=f[x];
	f[x]=findf(f[x]);
	dis[x]+=dis[orif];
	return f[x];
}
void combine(int x,int y)//合并操作
{
	int fx=findf(x),fy=findf(y);
	f[fx]=++cnt;
	f[fy]=cnt;
	dis[fx]=dis[fy]=dis[cnt]=0;
}
void add(int x,int s)//发送信息操作
{
	int fx=findf(x);
	f[fx]=++cnt;
	dis[fx]=s;
	dis[cnt]=0;
}
int main()
{
	init();
	cin>>n>>m;
	for(int i=1;i<=m;i++)
	{
		cin>>opt>>a>>b;
		if(opt==1)combine(a,b);
		else add(a,b);
	}
	for(int i=1;i<=n;i++)
	{
		findf(i);//更新距离
		cout<<dis[i]<<' ';
	}
	return 0;
}