P6429 [COCI2008-2009#1] JEZ 题解

题目传送门：Click。

更好地观感：Click（进入速度玄学）

某蒟蒻看见这道题，想了足足一个晚上，过后茅塞顿开，故作此篇。

感谢神犇的题解，思路基本相同，补充了一些自己的想法或这片题解可能没有注意到的细节。

看题目数据范围：\(1 \leqslant r,c \leqslant 10^6,1 \leqslant k \leqslant 10^{12}\)，显然打暴力 \(\mathcal{O}(rc)\) 的时间复杂度是行不通的。必须做到近似于 \(\mathcal{O}(r)\) 的时间复杂度。

观察题目：题目中说：当 \(x+y=x \oplus y\) 时，这个格子是灰色的。而最后所求的答案就是走过的灰色的格子数，很容易想到斜着划分所有的格子，每一组的格子中的任意一个格子 \((x,y)\) 都满足 \(x+y=S\)，其中 \(S\) 是不变的。如下图：（图可能有点丑，仅做示意）

接下来，我们针对某个特定的 \(S\) 进行考虑。设有一组 \((x,y)\)，那么 \(x \oplus y=S\) 必然满足：\(S\) 二进制上的第 \(x\) 位为 \(1\)，则 \(x\) 与 \(y\) 的二进制第 \(x\) 位上必然不同；而当 \(S\) 二进制上的第 \(x\) 位为 \(0\)，那么 \(x\) 与 \(y\) 二进制第 \(x\) 位上必然相同。

再来考虑加法。首先看 \(S\) 二进制位的最后一个 \(1\)，发现它有两种情况，通过后两位进位，或是由 \(x,y\) 中一个 \(0\) 一个 \(1\) 相加而成。

当它是通过后两位进位而成时，则 \(x,y\) 该位上相同则无法满足异或；不同，则无法满足相加（因为有进位）。（见下图 1）

而它是由更前面的某一位 \(0\) 对应的 \(x,y\) 中的 \(1\)，也无法满足要求。（见下图 2）

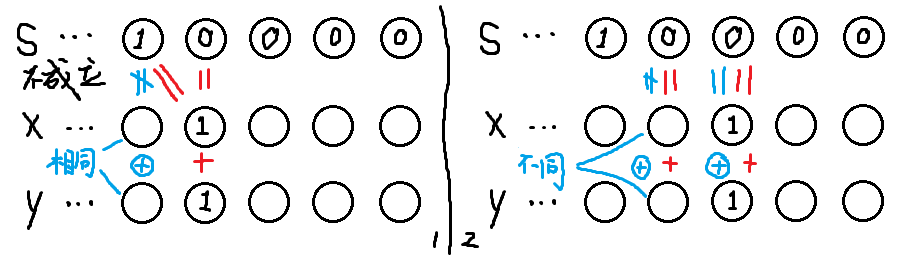
对于一个 \(S\)，我们可以把它分为若干如上形式的二进制段，也可得出相通的结论。综上，在 \(S\) 的每一位 \(0\) 上，\(x\) 与 \(y\) 同为 \(0\) ；否则，\(x,y\) 有且仅有一个 \(1\)。

从这一点入手，统计某一斜行（由于斜行上各自数量可能不确定，我们这里用两个数确定一斜行 \((x,y)\) 表示从 \((0,y)\) 走到 \((x,y-x)\)）上有多少个灰色格子（即 \(S=y\)），我们可以知道有一个 \(x^\prime \leqslant x\)，其中 \(x^\prime\) 二进制上的每一位 \(1\)，都对应了 \(x\) 与 \(y\) 上公共的 \(1\)。在这个 \(x^\prime\) 中，（对于一对二元组 \((p,q)\)，这一步相当于枚举 \(x\) 的二进制位）我们可以知道 \(p\) 可以在这一位上取 \(1\)（\(q\) 取 \(0\)），或者取 \(0\)（\(q\) 相反）。而对于 \(y\) 某二进制位上为 \(1\)，而 \(x\) 该二进制位上不为 \(1\)，那么只可能 \(q\) 上取 \(1\)，而 \(p\) 上为 \(0\)。

简单地说，就是将 \(y\) 分解成若干段形如 \(\texttt{1000...}\) 的二进制段，然后判断这些“段”与 \(x\) 是否对应。如果其最高位 \(1\) 与 \(x\) 对应，那么说明这一位可以 \(1\)，答案加上后面的几段（注意！这里并不要求与 \(x\) 对应！）分别取 \(0\) 或 \(1\) 的总方案数。当然，这样算会少算一种情况，即所有对应二进制段上都取了 \(0\)。

理解了这个规律，我们可以写出这样一个用来统计某一斜行上灰色格子数量的函数：

ll type[64];
ll counting(ll x,ll y) {
	ll res=1LL,cnt=0;
	for(;y;res<<=1,y>>=1)
		if(y&1) type[++cnt]=res;
	res=0;
	for(ll i=cnt;i>0;--i)
		if(x-type[i]>=0) x-=type[i],res|=(1<<i-1);
	return res+1;
}

解释说明：\(\operatorname{type}_i\) 表示 \(y\) 从高到低第 \(i\) 个 \(1\) 的权值。由于下标就相当于第几段，然后直接一边分解 \(x\) 一边计算答案就行了。1<<i-1 表示第 \(i\) 段后面有 \(i-1\) 段，每段取或不取的总方案数为 \(2^{i-1}\)，由于每个二进制位都不会重复，可以直接用 |= 运算。

最后回到问题，统计走 \(k\) 步走过的灰色格子数，可以先统计从如下图红色部分的斜行的灰色格子数，然后统计如下图绿色部分的灰色格子数，累加走过的格子。当走不完某一斜行时，暴力模拟一下就可以了。这里细节有点多，就不赘述了。

（其中灰色部分可以帮助统计绿色部分）

完整代码：

#include <bits/stdc++.h>
using namespace std;

typedef long long ll;
ll type[64];
ll counting(ll x,ll y) {
	ll res=1LL,cnt=0;
	for(;y;res<<=1,y>>=1)
		if(y&1) type[++cnt]=res;
	res=0;
	for(ll i=cnt;i>0;--i)
		if(x-type[i]>=0) x-=type[i],res|=(1<<i-1);
	return res+1;
}
ll n,m,k;

int main() {
	scanf("%lld%lld%lld",&n,&m,&k);
	int drct=1;
	if(m<n) swap(m,n),drct=0;
	ll ans=0,done=0;
	for(ll i=0;i<m;++i,drct^=1) {
		ll cnt=min(i+1,n);
		if(done+cnt<k) done+=cnt,ans+=counting(min(i,n-1),i);
		else {
			if(drct) for(ll p=min(i,n-1),q=i-min(i,n-1);done<k;--p,++q,++done)
				ans+=p+q==(p^q);
			else for(ll p=0,q=i;done<k;++p,--q,++done)
				ans+=p+q==(p^q);
			break;
		}
	}
	if(done==k) {
		printf("%lld\n",ans);
		return 0;
	}
	for(int i=1;i<n;++i,drct^=1) {
		ll cnt=n-i;
		if(done+cnt<k) done+=cnt,ans+=counting(n-1,m+i-1)-counting(i-1,m+i-1);
		else {
			if(drct) for(ll p=n-1,q=m-n+i;done<k;--p,++q,++done)
				ans+=p+q==(p^q);
			else for(ll p=i,q=m-1;done<k;++p,--q,++done)
				ans+=p+q==(p^q);
			break;
		}
	}
	printf("%lld\n",ans);
	return 0;
}

完。