2018 CCPC 吉林站 H Lovers || HDU 6562 (线段树哦)

http://acm.hdu.edu.cn/showproblem.php?pid=6562

题意：

q次操作

1.将第l~r个数的左边和和右边都加上一个数d， 使得这个数变成 dsiddsid的形式

2.询问区间和.

题解:对于一个数字x若执行第一个操作则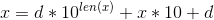  

则若对于一个区间sum(l,r)执行第一个操作则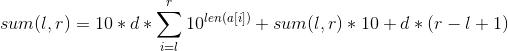  

设 

则便可以用线段树去维护这两个东西便可,这里只考虑了d是一位数的情况,但是在线段树下传标记的过程中可能一个区间多次执行第一个操作,那么wrap的d便不是一位数,而且左右两边的d是镜像的,我们便要用两个lazy标记,lazy1维护左边加的数,lazy2维护右边加的数,同时可以用lazylen表示这两个lazy的,然后好好考虑一下如何维护sum和sumlen即可

个人感悟：在敲的时候思路是基本对的 ， 但是我在维护 的时候 为了计算10的多少次幂,我维护的是一个长度 ，然后查询的时候，用一个阶乘的fac10[]数组 ， 果然RE了 ， 大神的代码， 发现别人维护的是一个10^（len）的值，其实细想也是，我们主要维护的就是这个，我居然多次了一举，太菜了我

#include <iostream>
#include <string.h>
#include <algorithm>
#include <stdio.h>
#include <math.h>
#include <queue>
#define MAXN 400010
#define inf 0x3f3f3f3f
#define LL long long
using namespace std;
const int N=1e7+;
const int mod = 1e9+;
struct node{
    int l,r; //区间[l,r]
    LL addl,addr; //区间的延时标记
    LL sum,laz,all; /// 区间和 laz增加位数 all=10^位数
}tree[MAXN<<];//一定要开到4倍多的空间
void pushup(int index) {
    tree[index].sum = (tree[index<<].sum+tree[index<<|].sum)%mod;
    tree[index].all = (tree[index<<].all+tree[index<<|].all)%mod;
}
void pushdown(int index) {
    if(tree[index].laz > ) {
        tree[index<<].addl = (tree[index].addl*tree[index<<].laz%mod + tree[index<<].addl%mod)%mod;
        tree[index<<|].addl = (tree[index].addl*tree[index<<|].laz%mod + tree[index<<|].addl%mod)%mod;

        tree[index<<].addr = (tree[index<<].addr*tree[index].laz%mod + tree[index].addr%mod)%mod;
        tree[index<<|].addr = (tree[index<<|].addr*tree[index].laz%mod+ tree[index].addr)%mod;

        tree[index<<].sum = (( tree[index<<].sum*tree[index].laz%mod
                            + tree[index].addl*tree[index<<].all%mod*tree[index].laz%mod)%mod
                            + tree[index].addr*(tree[index<<].r-tree[index<<].l+)%mod)%mod;
        tree[index<<|].sum = ((tree[index<<|].sum*tree[index].laz%mod
                            + tree[index].addl*tree[index<<|].all%mod*tree[index].laz%mod)%mod
                            + tree[index].addr*(tree[index<<|].r-tree[index<<|].l+)%mod)%mod;

        tree[index<<].all = (tree[index<<].all*tree[index].laz%mod*tree[index].laz)%mod;
        tree[index<<|].all = (tree[index<<|].all*tree[index].laz%mod*tree[index].laz)%mod;
        tree[index<<].laz = tree[index].laz*tree[index<<].laz%mod;
        tree[index<<|].laz = tree[index].laz*tree[index<<|].laz%mod;
        tree[index].laz = ;

        tree[index].addl = ;
        tree[index].addr = ;
    }

}
void build(int l,int r,int index){
    tree[index].sum = ;
    tree[index].l = l; tree[index].r = r;
    tree[index].addl = tree[index].addr = ;
    tree[index].laz = ;//刚开始一定要清0
    if(l == r) {
        tree[index].all = ;
        return ;
    }
    int mid = (l+r)>>;
    build(l,mid,index<<);
    build(mid+,r,index<<|);
    pushup(index);
}
void update(int l,int r,int index,LL val) {
    if(l <= tree[index].l && r >= tree[index].r) {
        tree[index].sum = ((tree[index].sum*%mod
                            + val*(tree[index].r-tree[index].l+)%mod)%mod
                            + val**tree[index].all %mod )%mod ;
        tree[index].all = tree[index].all*%mod;
        tree[index].addl = (val*tree[index].laz%mod + tree[index].addl)%mod;
        tree[index].laz = tree[index].laz*%mod;
        tree[index].addr = (tree[index].addr*%mod + val)%mod;
        return ;
    }
    pushdown(index);
    int mid = (tree[index].l+tree[index].r)>>;
    if(l <= mid) update(l,r,index<<,val);
    if(r > mid) update(l,r,index<<|,val);
    pushup(index);
}
LL query(int l,int r,int index) {
    if(l <= tree[index].l && r >= tree[index].r) {
        return tree[index].sum;
    }
    pushdown(index);
    int mid = (tree[index].l+tree[index].r)>>;
    LL ans = ;
    if(l <= mid) ans = (ans+query(l,r,index<<))%mod;
    if(r > mid) ans = (ans+query(l,r,index<<|))%mod;
    return ans;
}
int main()
{
    int _; scanf("%d",&_);
    for(int ncase=;ncase<=_;ncase++) {
        int n,m; scanf("%d%d",&n,&m);
        printf("Case %d:\n",ncase);
        build(,n,);
        while(m--) {
            char s[]; scanf("%s",s);
            int l,r,v; scanf("%d%d",&l,&r);
            if(s[]=='w') {
                scanf("%d",&v); update(l,r,,v);
            } else {
                printf("%lld\n",query(l,r,));
            }
        }
    }
    return ;
}