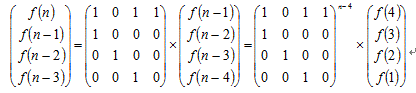hdu 2604 Queuing(推推推公式+矩阵快速幂)
Description
Now we define that ‘f’ is short for female and ‘m’ is short for male. If the queue’s length is L, then there are 2
L numbers of queues. For example, if L = 2, then they are
ff, mm, fm, mf .
O-queue else it is a E-queue.
Your task is to calculate the number of E-queues mod M with length L by writing a program.
Input
6) and M.
Output
Sample Input
3 8
4 7
4 8
Sample Output
6
2
1 给你一个只有f和m,长度为l的字符串,让你找出满题条件的串的个数对m取余的数。如果这个串中不含fff和fmf就说这个串是满足条件的。
假设现有长度为n的串s,f(n)是s串满足条件的答案。f(n)怎么推出来捏?
如果s的最后一位为m,那么就加上f(n-1),因为在长度为n-1的满足条件的串后面加上一个m所得到的串肯定也满足条件。
如果s的最后一位为f,那么s的最后三位只有mmf和mff两种情况!继续讨论!
如果s以mmf结尾,那么加上f(n-3),因为在长度为n-3的满足条件的串后面加上一个mmf所得到的串肯定也满足条件。
那如果s以mff结尾呢?向前思考一位,倒数第四位只能是m,也就是此时s是以mmff结尾的,再加上f(n-4)岂不是美滋滋?
综上f(n)=f(n-1)+f(n-3)+f(n-4)。无耻的再盗张图...OTZ...
代码如下:
#include <bits/stdc++.h> using namespace std;
const int N=;
int l,m;
struct Matrix
{
long long int mat[N][N];
}matrix;
void init()
{
memset(matrix.mat,,sizeof matrix.mat);
matrix.mat[][]=;
matrix.mat[][]=;
matrix.mat[][]=;
matrix.mat[][]=;
for (int i=;i<N;++i)
{
for (int j=;j<N;++j)
{
if (i==j+)
matrix.mat[i][j]=;
}
}
}
Matrix operator * (Matrix a,Matrix b)
{
Matrix c;
for (int i=;i<N;++i)
{
for (int j=;j<N;++j)
{
c.mat[i][j]=;
for (int k=;k<N;++k)
c.mat[i][j]+=a.mat[i][k]*b.mat[k][j];
c.mat[i][j]%=m;
}
}
return c;
}
Matrix Pow (int n)
{
Matrix t;
if (n==)
return matrix;
if (n&)
return matrix*Pow(n-);
else
{
Matrix temp=Pow(n>>);
return temp*temp;
}
}
int main()
{
//freopen("de.txt","r",stdin);
long long int f[];
f[]=;
f[]=;
f[]=;
f[]=;
f[]=;
while (~scanf("%d%d",&l,&m))
{
init();
if (l<=)
{
printf("%lld\n",f[l]%m);
continue;
}
Matrix temp=Pow(l-);
long long int ans=;
for (int i=;i<N;++i)
{
ans += temp.mat[][i]*f[N-i];
ans%=m;
}
printf("%lld\n",ans);
}
return ;
}
hdu 2604 Queuing(推推推公式+矩阵快速幂)的更多相关文章
- CCF 201312-4 有趣的数 (数位DP, 状压DP, 组合数学+暴力枚举, 推公式, 矩阵快速幂)
问题描述 我们把一个数称为有趣的,当且仅当: 1. 它的数字只包含0, 1, 2, 3,且这四个数字都出现过至少一次. 2. 所有的0都出现在所有的1之前,而所有的2都出现在所有的3之前. 3. 最高 ...
- HDU6050: Funny Function(推公式+矩阵快速幂)
传送门 题意 利用给出的式子求\(F_{m,1}\) 分析 直接推公式(都是找规律大佬) \(n为偶数,F_{m,1}=\frac{2(2^n-1)^{m-1}}3\) \(n为奇数,F_{m,1}= ...
- HDU 2855 斐波那契+矩阵快速幂
http://acm.hdu.edu.cn/showproblem.php?pid=2855 化简这个公式,多写出几组就会发现规律 d[n]=F[2*n] 后面的任务就是矩阵快速幂拍一个斐波那契模板出 ...
- HDU 5950:Recursive sequence(矩阵快速幂)
http://acm.hdu.edu.cn/showproblem.php?pid=5950 题意:给出 a,b,n,递推出 f(n) = f(n-1) + f(n-2) * 2 + n ^ 4. f ...
- HDU 3292 【佩尔方程求解 && 矩阵快速幂】
任意门:http://acm.hdu.edu.cn/showproblem.php?pid=3292 No more tricks, Mr Nanguo Time Limit: 3000/1000 M ...
- 【66测试20161115】【树】【DP_LIS】【SPFA】【同余最短路】【递推】【矩阵快速幂】
还有3天,今天考试又崩了.状态还没有调整过来... 第一题:小L的二叉树 勤奋又善于思考的小L接触了信息学竞赛,开始的学习十分顺利.但是,小L对数据结构的掌握实在十分渣渣.所以,小L当时卡在了二叉树. ...
- HDU 2256 Problem of Precision 数论矩阵快速幂
题目要求求出(√2+√3)2n的整数部分再mod 1024. (√2+√3)2n=(5+2√6)n 如果直接计算,用double存值,当n很大的时候,精度损失会变大,无法得到想要的结果. 我们发现(5 ...
- HDU 2256 Problem of Precision (矩阵快速幂)(推算)
Problem of Precision Time Limit: 1000/1000 MS (Java/Others) Memory Limit: 32768/32768 K (Java/Oth ...
- hdu3483 A Very Simple Problem 非线性递推方程2 矩阵快速幂
题目传送门 题目描述:给出n,x,mod.求s[n]. s[n]=s[n-1]+(x^n)*(n^x)%mod; 思路:这道题是hdu5950的进阶版.大家可以看这篇博客hdu5950题解. 由于n很 ...
随机推荐
- TCP/IP 协议是如何保证数据可靠性的?
原文: 网络基础:TCP协议-如何保证传输可靠性 TCP协议传输的特点主要就是面向字节流.传输可靠.面向连接.这篇博客,我们就重点讨论一下TCP协议如何确保传输的可靠性的. 确保传输可靠性的方式TCP ...
- selenium自动化测试工具模拟登陆爬取当当网top500畅销书单
selenium自动化测试工具可谓是爬虫的利器,基本动态加载的网页都能抓取,当然随着大型网站的更新,也出现针对selenium的反爬,有些网站可以识别你是否用的是selenium访问,然后对你加以限制 ...
- 04 Redis主从同步
redis主从同步 原理:1. 从服务器向主服务器发送 SYNC 命令.2. 接到 SYNC 命令的主服务器会调用BGSAVE 命令,创建一个 RDB 文件,并使用缓冲区记录接下来执行的所有写命令.3 ...
- day3-3种实现小图标与文字水平对齐的方式
效果图: 1.使用小图标作为背景图实现 html: <div class="test"> <ul> <li class="method1&q ...
- hiper、sitespeed性能工具
https://github.com/pod4g/hiper hiper: A statistical analysis tool for performance testing https: ...
- linux系统awk命令
awk是行处理器: 相比较屏幕处理的优点,在处理庞大文件时不会出现内存溢出或是处理缓慢的问题,通常用来格式化文本信息awk处理过程:?依次对每一行进行处理,然后输出awk命令形式:awk [-F|-f ...
- redis一键部署脚本
1.新建一个名为 auto_install_redis.sh的文件 2.将下面脚本拷贝到文件中,具体步骤在注释里面 #环境 linux #一键安装redis,在linux环境中使用脚本运行该文件(sh ...
- Darknet版YOLO安装与配置
Darknet配置和安装 1. 安装显卡驱动 首先查看一下自己的电脑需要怎样的驱动,我们可以先到 http://www.nvidia.com/Download/index.aspx 查询下我们需要的是 ...
- python-迭代器与生成器1
python-迭代器与生成器1 迭代器与生成器列表的定义列表生成式:作用使代码更加简洁通过列表生成式,我们可以直接创建一个列表.但是,受到内存限制,列表容量肯定是有限的.而且,创建一个包含100万个元 ...
- SpringBoot核心特性之组件自动装配
写在前面 spring boot能够根据依赖的jar包自动配置spring boot的应用,例如: 如果类路径中存在DispatcherServlet类,就会自动配置springMvc相关的Bean. ...