HDU 6073 Matching In Multiplication —— 2017 Multi-University Training 4

Matching In Multiplication

Time Limit: 6000/3000 MS (Java/Others)    Memory Limit: 524288/524288 K (Java/Others)
Total Submission(s): 1389    Accepted Submission(s): 423

Problem Description

In the mathematical discipline of graph theory, a bipartite graph is a graph whose vertices can be divided into two disjoint sets U and V (that is, U and V are each independent sets) such that every edge connects a vertex in U to one in V. Vertex sets U and V are usually called the parts of the graph. Equivalently, a bipartite graph is a graph that does not contain any odd-length cycles. A matching in a graph is a set of edges without common vertices. A perfect matching is a matching that each vertice is covered by an edge in the set.

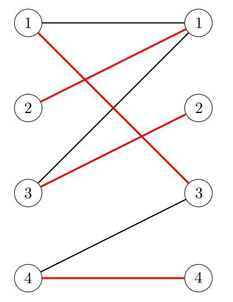
Little Q misunderstands the definition of bipartite graph, he thinks the size of U is equal to the size of V, and for each vertex p in U, there are exactly two edges from p. Based on such weighted graph, he defines the weight of a perfect matching as the product of all the edges' weight, and the weight of a graph is the sum of all the perfect matchings' weight.

Please write a program to compute the weight of a weighted ''bipartite graph'' made by Little Q.

 

Input

The first line of the input contains an integer T(1≤T≤15), denoting the number of test cases.

In each test case, there is an integer n(1≤n≤300000) in the first line, denoting the size of U. The vertex in U and V are labeled by 1,2,...,n.

For the next n lines, each line contains 4 integers vi,1,wi,1,vi,2,wi,2(1≤vi,j≤n,1≤wi,j≤109), denoting there is an edge between Ui and Vvi,1, weighted wi,1, and there is another edge between Ui and Vvi,2, weighted wi,2.

It is guaranteed that each graph has at least one perfect matchings, and there are at most one edge between every pair of vertex.

 

Output

For each test case, print a single line containing an integer, denoting the weight of the given graph. Since the answer may be very large, please print the answer modulo 998244353.

 

Sample Input

1

2

2 1 1 4

1 4 2 3

 

Sample Output

16

 

题意：左右两边各有n个顶点的集合，分别为U，V，从U的每个顶点会有连出两条带权边与V的顶点相连。题目要求我们选取若干条边，使两个集合的所有点得到覆盖，并且定义这种情况为“完美匹配“，”完美匹配“的值为所选取的边权值求积，最后输出所有完美匹配的值之和。

 

思路：首先对于V的所有点来说，入度为1的点一定在U集合有唯一的点与之相连，在每种”完美匹配“里它们的配对是固定的，于是就可以扫一遍所有唯一对应的点对，求出它们的边权之积 left。

在排除以上情况的点之后，U集合点的出度均为2，假如V集合存在入度大于2的点，必存在另外有个点入度小于2。然而这是不可能的，否则就和上一种情况矛盾。所以剩余V集合里的点入度均为2，剩余的边构成了环。接着间隔取点，每个环的”完美匹配“结果分两种s[0], s[1]，求出所有s[0]+s[1], 与left相乘取模得到结果。(补题时没好好理解题意，把相乘写成相加了（/TДT)/)

 

AC代码:

 #include<iostream>
 #include<cstring>
 #include<cstdio>
 #include<vector>
 #include<fstream>
 #include<queue>
 using namespace std;
 typedef long long LL;
 const int MAXN=6e5+;
 const int N=3e5;
 const LL MOD=;
 struct Edge{
     int to;
     LL w;
 };
 vector<Edge> edge[MAXN];
 int deg[MAXN];
 LL s[];
 void dfs(int node,int pos, bool ext){
     //cout<<node<<' '<<s[0]<<' '<<s[1]<<' '<<deg[node]<<' '<<ext<<endl;
     for(int i=;i<edge[node].size();i++){
         int p=edge[node][i].to;
         if(!deg[p])
             continue;

         if(deg[p]==)
         {
             deg[node]--;
             deg[p]--;
             s[pos]=s[pos]*edge[node][i].w%MOD;
             dfs(p, pos^, ext);
             break;
         }
         else if(deg[node]==&&deg[p]==)
         {
             if(ext==false)
                 ext=true;
             else{
                 deg[node]--;
                 deg[p]--;
                 s[pos]=s[pos]*edge[node][i].w%MOD;
                 return;
             }
         }
     }
 }

 int main()
 {
     //ifstream cin("ylq.txt");
     int T;
     cin>>T;
     int n,v1,v2;
     LL w1,w2;
     Edge e1,e2;
     while(T--)
     {
         memset(deg, , sizeof(deg));
         //cin>>n;
         scanf("%d", &n);
         for(int i=;i<=N+n;i++){
             edge[i].clear();
         }
         for(int i=;i<=n;i++){
             //cin>>v1>>w1>>v2>>w2;
             scanf("%d %lld %d %lld", &v1, &w1, &v2, &w2);
             deg[v1+N]++;
             deg[v2+N]++;
             deg[i]+=;

             e1.to=v1+N;e1.w=w1;
             e2.to=v2+N;e2.w=w2;
             edge[i].push_back(e1);
             edge[i].push_back(e2);

             e1.to=i;e2.to=i;
             edge[v1+N].push_back(e1);
             edge[v2+N].push_back(e2);
         }

         LL left=;
         queue<int> q;
         for(int i=N;i<=n+N;i++)
             if(deg[i]==)
                 q.push(i);

         int m;
         while(!q.empty())
         {
             int p, pp;
             m=q.front(); q.pop();
             deg[m]=;
             for(int i=;i<edge[m].size();i++){
                 p=edge[m][i].to;
                 if(!deg[p])
                     continue;
                 else
                 {
                     deg[p]=;
                     left=left*edge[m][i].w%MOD;
                     for(int k=;k<edge[p].size();k++){
                         pp=edge[p][k].to;
                         if(deg[pp]==) continue;

                         deg[pp]--;
                         if(deg[pp]==)
                             q.push(pp);
                     }
                 }
             }

         }
         //cout<<'*'<<left<<'*'<<endl;
         LL ans=left;
         for(int i=;i<=n;i++){
             if(!deg[i])
                 continue;
             s[]=s[]=;
             dfs(i, , );
             ans=ans*(s[]+s[])%MOD;
         }

         printf("%lld\n", ans);
     }
 }

我的代码里用入度出度判断是否走到重复点，看了好多人都是用vis判断的，感觉都差不多。。。。