Linear Regression and Gradient Descent (English version)
1.Problem and Loss Function
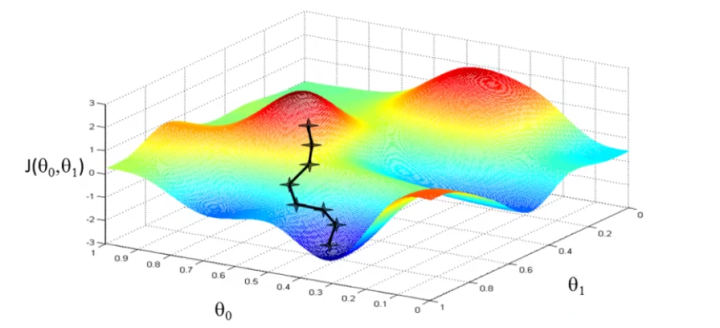
From the initial state, we probably have a really poor system (may be only output zero). By using X and Y to train, we try to derive a better parameter θ. The training process (learning process) may be time-consuming, because the algorithm updates parameters only a little on every training step.
2. Cost Function?
Suppose driving from somewhere to Toronto: it is easy to know the coordinates of Toronto, but it is more important to know where we are now! Cost function is the tool giving us how different between Hypothesis and label Y, so that we can drive to the target. For regression problem, we use MSE as the cost function.
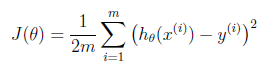

Linear Regression and Gradient Descent (English version)的更多相关文章
- Linear Regression Using Gradient Descent 代码实现
参考吴恩达<机器学习>, 进行 Octave, Python(Numpy), C++(Eigen) 的原理实现, 同时用 scikit-learn, TensorFlow, dlib 进行 ...
- 线性回归、梯度下降(Linear Regression、Gradient Descent)
转载请注明出自BYRans博客:http://www.cnblogs.com/BYRans/ 实例 首先举个例子,假设我们有一个二手房交易记录的数据集,已知房屋面积.卧室数量和房屋的交易价格,如下表: ...
- 斯坦福机器学习视频笔记 Week1 Linear Regression and Gradient Descent
最近开始学习Coursera上的斯坦福机器学习视频,我是刚刚接触机器学习,对此比较感兴趣:准备将我的学习笔记写下来, 作为我每天学习的签到吧,也希望和各位朋友交流学习. 这一系列的博客,我会不定期的更 ...
- 斯坦福机器学习视频笔记 Week1 线性回归和梯度下降 Linear Regression and Gradient Descent
最近开始学习Coursera上的斯坦福机器学习视频,我是刚刚接触机器学习,对此比较感兴趣:准备将我的学习笔记写下来, 作为我每天学习的签到吧,也希望和各位朋友交流学习. 这一系列的博客,我会不定期的更 ...
- Linear Regression and Gradient Descent
随着所学算法的增多,加之使用次数的增多,不时对之前所学的算法有新的理解.这篇博文是在2018年4月17日再次编辑,将之前的3篇博文合并为一篇. 1.Problem and Loss Function ...
- Logistic Regression and Gradient Descent
Logistic Regression and Gradient Descent Logistic regression is an excellent tool to know for classi ...
- Logistic Regression Using Gradient Descent -- Binary Classification 代码实现
1. 原理 Cost function Theta 2. Python # -*- coding:utf8 -*- import numpy as np import matplotlib.pyplo ...
- flink 批量梯度下降算法线性回归参数求解(Linear Regression with BGD(batch gradient descent) )
1.线性回归 假设线性函数如下: 假设我们有10个样本x1,y1),(x2,y2).....(x10,y10),求解目标就是根据多个样本求解theta0和theta1的最优值. 什么样的θ最好的呢?最 ...
- machine learning (7)---normal equation相对于gradient descent而言求解linear regression问题的另一种方式
Normal equation: 一种用来linear regression问题的求解Θ的方法,另一种可以是gradient descent 仅适用于linear regression问题的求解,对其 ...
随机推荐
- 【问题解决方案】GitHub的md中使用库中图片
参考链接: 在GitHub中使用图片功能 步骤: 在github上的仓库建立一个存放图片的文件夹,文件夹名字随意.如:image 将需要在插入到文本中的图片,push到image文件夹中. 然后打开g ...
- surpace pro 检测维修记录
1.大陆不在全球联保范围内. 2.不要升级系统(win 10 1709)容易键盘失去反应. 3.不要乱安装系统,官方有回复镜像包,记住系列号, 4.大陆没有维修的点,有问题着官方服务, 5.uefi设 ...
- 微信小程序(1)--新建项目
这些天看了一下最近特别火的微信小程序,发现和vue大同小异. 新建项目 为方便初学者了解微信小程序的基本代码结构,在创建过程中,如果选择的本地文件夹是个空文件夹,开发者工具会提示,是否需要创建一个 q ...
- Vue:子组件如何跟父组件通信
我们知道,父组件使用 prop 传递数据给子组件.但子组件怎么跟父组件通信呢?这个时候 Vue 的自定义事件系统就派得上用场了. 使用 v-on 绑定自定义事件 每个 Vue 实例都实现了事件接口,即 ...
- 解决IDEA项目名称无下标蓝色小方块
点击下图中 + 号,引入该工程的pom.xml即可 .
- python输出转义字符
转义字符在字符串中不代表自己,比如\n代表回车,不代表\n字符,那我想输入转义字符本身呢? 答:在字符串前面加个r 如print(“aa\nbb”) 会输出aa bb 如print(r"aa ...
- react-jsx和数组
JSX: 1.全称:JavaScriptXML, 2.react定义的一种类似于XML的JS扩展语法:XML+JS 3.作用:用来创建react虚拟DOM(元素)对象 var ele=<h1&g ...
- MySQL入门常用命令
使用本地 MySQL,系统 Ubuntu. mysql -u root -p 输入 root 用户的密码进入MySQL: mysql>
- noteone
- Web核心之最简单最简单最简单的登录页面
需求分析: 在登录页面提交用户名和密码 在Servlet中接收提交的参数,封装为User对象,然后调用DAO中的方法进行登录验证 在DAO中进行数据库查询操作,根据参数判断是否有对象的用户存在 在Se ...
