Catalan数列

引入

　　　　今天听学长讲了卡特兰数列后对其有了更深的认识，在此完善了一下之前的博客加以总结。

　　　　首先用一个经典的例子来描述一下Catalan数列，我们有一个1~n的数列和一个大小为n的栈，我们有如下两种操作：

1. 1. 1. 当未入栈序列不为空时，使序列的第一个元素入栈。
      2. 当栈不为空时，使栈顶元素出栈。

　　　　我们可以显然地发现，如果我们选择操作的顺序不同，我们最后所形成的出栈序列也不相同，那么有多少种出栈序列呢？

　　

　　　　而这个数列中的C（n），就是我们所定义的Catalan数列。

　　　　如果我们把所有每一次的操作都写出来，可以得到一个关于1和2的操作序列，这个序列有以下性质：

1. 1. 共有2n项且n项为1，n项为2。
   2. 从左往右1的个数永远不少于2的个数。

定义

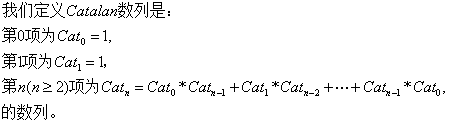
通项公式

　　

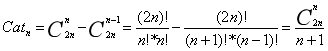
通项公式推导

　　方法1：数学方法，摘自某大老的PPT，表示不是很了解，在此向各位大佬请教。

---

---

---

即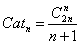（注意他证明过程中的初值是）

---

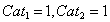　　方法2:组合数证明法

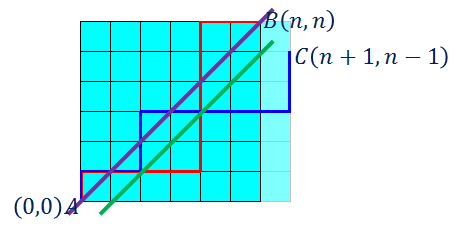
　　我们设定一个情景：假设一个点从A（0,0）出发走到B（n，n），我们定义两种走的方法：

1. 1. 往右走。
   2. 往上走。

　　我们从A走到B，一共要走2n步，其中n步为1,n步为2，这样我们从A走到B的方案也就可以转化为一个1和2的序列了，而所有的1和2的序列构成的排列，即为从A走到B的方案数：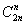

　　相较之于引言中所提到的序列，要使通过这种情景生成的序列是满足Catalan的数列的方案序列，我们需要的充要条件是从左往右1的个数永远比2的个数少（即向上走过的次数不少于向右走过的次数），即所走的路径只存在于紫线的上部，而这个条件等价于所形成的路径与绿线没有交点。我们已经知道了所有的方案数，我们只需要求出不满足条件的方案数就可以了。

　　举出一个反例（红线）我们把这条线与绿线的第一个交点之后的部分都关于绿线对称得到蓝线部分，加上前面的部分与之形成的路径构成了一条从A（0，0）走向C（n+1，n-1）的路径，我们可以发现这样的蓝线有以下三条性质：

1. 1. 蓝线只向上走和向右走，且重点为C（n+1，n-1）。
   2. 对于每一条符合性质1的蓝色路径都有且只有一条不合法的红色路径与之对应。
   3. 对于每一条不合法的红色路径有且只有一条满足性质1的蓝色路径与之对应。

　　由此，我们可以发现不合法的红色路径与满足上述性质的蓝色路径一一对应，所以不合法路径数就是蓝色路径数，为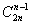

　　所以，所有合法的路径数为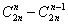：，即Catalan的第n个数为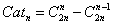

推论

• • n个左括号和n个右括号组成的合法括号序列的数量为Cat（n）。
  • 1,2，···，n经过一个栈，形成的合法出栈序列的数量为Cat（n）。
  • n个结点构成的不同二叉树的数量为Cat（n）。
  • 在平面直角坐标系上每一步只能向右或向上走，从（0,0）走到（n，n）并且除两个端点外不接触直线 y = x的路线数量为Cat（n）。
    • 推广：在平面直角坐标系上，每一步只能向右或上走一步，从（0,0）走到（n，m）（n ≥m）并且除两个点外不接触直线 y = x 的路线的数量为