Codeforces Round #361 (Div. 2) E. Mike and Geometry Problem 【逆元求组合数 && 离散化】

任意门：http://codeforces.com/contest/689/problem/E

E. Mike and Geometry Problem

time limit per test

3 seconds

memory limit per test

256 megabytes

input

standard input

output

standard output

Mike wants to prepare for IMO but he doesn't know geometry, so his teacher gave him an interesting geometry problem. Let's define f([l, r]) = r - l + 1 to be the number of integer points in the segment [l, r] with l ≤ r (say that 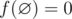). You are given two integers nand k and n closed intervals [li, ri] on OX axis and you have to find:

In other words, you should find the sum of the number of integer points in the intersection of any k of the segments.

As the answer may be very large, output it modulo 1000000007 (109 + 7).

Mike can't solve this problem so he needs your help. You will help him, won't you?

Input

The first line contains two integers n and k (1 ≤ k ≤ n ≤ 200 000) — the number of segments and the number of segments in intersection groups respectively.

Then n lines follow, the i-th line contains two integers li, ri ( - 109 ≤ li ≤ ri ≤ 109), describing i-th segment bounds.

Output

Print one integer number — the answer to Mike's problem modulo 1000000007 (109 + 7) in the only line.

Examples

input

Copy

3 2
1 2
1 3
2 3

output

Copy

5

input

Copy

3 3
1 3
1 3
1 3

output

Copy

3

input

Copy

3 1
1 2
2 3
3 4

output

Copy

6

Note

In the first example:

;

;

.

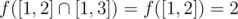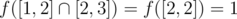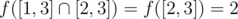So the answer is 2 + 1 + 2 = 5.

大概题意：

有 N 个区间， 从其中取 K 个区间。所以有 C（N， K）种组合， 求每种组合区间交集长度的总和。

解题思路：

丢开区间的角度，从每个结点的角度来看，其实每个结点的贡献是 C（cnt， K） cnt 为该结点出现的次数， 所以只要O（N）扫一遍统计每个结点的贡献就是答案。

思路清晰，但考虑到数据的规模，这里需要注意和需要用到两个技巧：

一是离散化，这里STL里的 vector 和 pair 结合用，结合区间加法的思想进行离散化。

二是求组合数时 除数太大，考虑到精度问题需要用逆元来计算。

AC code：

 #include<bits/stdc++.h>
 using namespace std;
 const int maxn = 2e5+;
 const int mod = 1e9+;
 long long fac[maxn];

 long long qpow(long long a,long long b)  //快速幂
 {
     long long ans=;a%=mod;
     for(long long i=b;i;i>>=,a=a*a%mod)
         if(i&)ans=ans*a%mod;
     return ans;
 }

 long long C(long long n,long long m)    //计算组合数
 {
     if(m>n||m<)return ;
     long long s1=fac[n], s2=fac[n-m]*fac[m]%mod;   //除数太大，逆元处理
     return s1*qpow(s2,mod-)%mod;
 }
 int n,k;
 int l[maxn],r[maxn];      //左端点， 右端点
 int main()
 {
     fac[]=;
     for(int i=;i<maxn;i++)     //预处理全排列
         fac[i]=fac[i-]*i%mod;

     scanf("%d%d",&n,&k);
     for(int i=;i<=n;i++){
         scanf("%d",&l[i]);
         scanf("%d",&r[i]);
     }
     vector<pair<int,int> >op;
     for(int i=;i<=n;i++){                //离散化
         op.push_back(make_pair(l[i]-,));  //区间加法标记
         op.push_back(make_pair(r[i],-));
     }
     sort(op.begin(),op.end());  //升序排序
     long long ans = ;          //初始化
     int cnt=;
     int la=-2e9;
     for(int i=;i<op.size();i++){                //计算每点的贡献
         ans=(ans+C(cnt,k)*(op[i].first-la))%mod;
         la=op[i].first;
         cnt+=op[i].second;                    //该点的前缀和就是该点的出现次数
     }
     cout<<ans<<endl;
 }