1. 时间复杂度（大O表示法）以及使用python实现栈

1.时间复杂度（大O表示法）：

　　　　O(1) < O(logn) < O(n) < O(nlogn) < O(n²) < O(n³) < O(2ⁿ) < O(n!) < O(nⁿ)

　　　

　　(1)Python中常用数据结构的时间复杂度：

　　　　　　list内置操作的时间复杂度：　　　　　　　　　　

　　　　　　　　

　　　　dict内置操作的时间复杂度：

　　　　　　

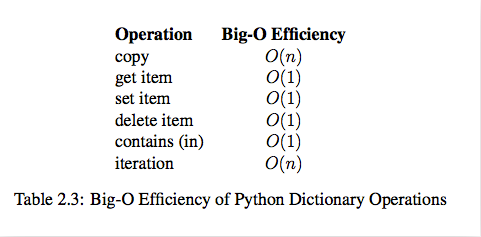
　　(2)抽象数据类型（ADT: Abstract Data Type）:

　　　　常用数据运算（5种）：

　　　　　　　增（插入）

　　　　　　　删（删除）

　　　　　　　改（修改）

　　　　　　　查（查找）

　　　　　　　排序

 

2. 栈的实现：

　　（1）栈的表现形式：

　　　　　

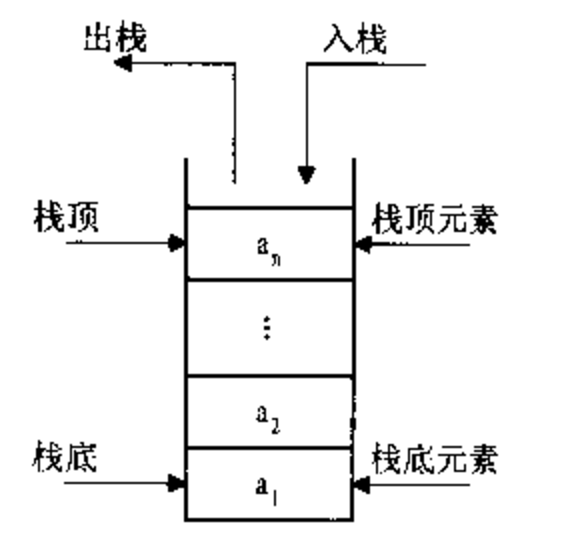
　　（2）栈的操作：

　　　　Stack():　   创建一个新的空栈

　　　　push(item):添加一个新元素item到栈顶

　　　　pop():　　  弹出栈顶元素

　　　　peek():　　 返回栈顶元素

　　　　is_empty(): 判断栈是否为空

　　　　size():　　   返回栈的元素个数

　　（3）实现栈：　　　　

 class Stack(object):
     """栈的实现"""
     def __init__(self):
         self.__list = []

     # 添加一个新元素item到栈顶
     def push(self, item):
         self.__list.append(item)

     # 弹出栈顶元素
     def pop(self):
         return self.__list.pop()

     # 返回栈顶元素
     def peek(self):
         if self.__list:
             return self.__list[-1]
         else:
             return None

     # 判断栈是否为空
     def is_empty(self):
         return self.__list == []

     # 返回栈的元素个数
     def size(self):
         return len(self.__list)

 if __name__ == "__main__":
     s = Stack()
     s.push(1)
     s.push(2)
     s.push(3)
     s.push(4)

     print(s.pop())
     print(s.pop())
     print(s.pop())
     print(s.pop())

　　　　　　运行结果：