（数据科学学习手札09）系统聚类算法Python与R的比较

上一篇笔者以自己编写代码的方式实现了重心法下的系统聚类（又称层次聚类）算法，通过与Scipy和R中各自自带的系统聚类方法进行比较，显然这些权威的快捷方法更为高效，那么本篇就系统地介绍一下Python与R各自的系统聚类算法；

Python

cluster是Scipy中专门用来做聚类的包，其中包括cluster.vq矢量量化包，里面封装了k-means方法，还包括cluster.hierarchy，里面封装了层次聚类和凝聚聚类的方法，本文只介绍后者中的层级聚类方法，即系统聚类方法，先从一个简单的小例子出发：

import scipy
import scipy.cluster.hierarchy as sch
import matplotlib.pylab as plt
import numpy as np
 
price = [1.1,1.2,1.3,1.4,10,11,20,21,33,34]
increase = [1 for i in range(10)]
X = np.array([price,increase],dtype='float32')
X = X.T#这里必须使得输入的矩阵行代表样本，列代表维度
 
d = sch.distance.pdist(X)#计算样本距离矩阵
 
Z = sch.linkage(d, method='complete')#进行层级聚类，这里complete代表层级聚类中的最长距离法
 
sch.dendrogram(Z)#显示树状聚类图

生成的树状聚类图如下：

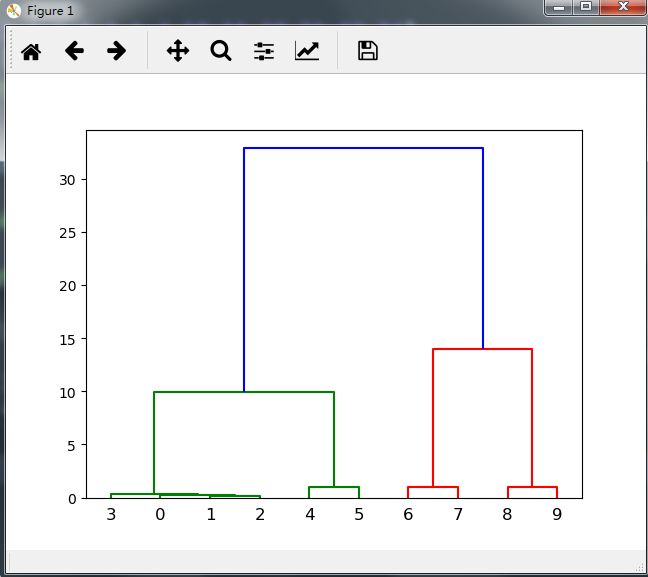
sch.distance.pdist(X,'method')：计算样本的距离阵，默认使用'euclidean',即欧氏距离法来计算距离，常用的其他可选择的距离计算方法有：'minkowski'，即使用明氏距离法，若使用该方法，需额外添加参数p=n，其中n为范数的方式，取2时即为欧氏距离法；'cityblock'，曼哈顿距离，即出租车距离，是一种衡量特殊距离的方法，计算的是数据对应坐标的直接差距而不进行范数处理；'seuclidean'，计算标准化后的欧氏距离，具体计算方法参照帮助手册；'sqeuclidean'，计算平方后的欧氏距离；'cosine'，计算变量间的余弦距离，这在R型聚类中经常使用；'correlation'，计算变量间的相关距离，这也是R型聚类中经常使用的；'chebyshev'，计算切比雪夫距离；'mahalanobis'，计算马氏距离，这是系统聚类中常用的方法，它的优点是即排除了各指标间的相关性干扰，又消除了各指标的量纲。以上就是常用的距离计算方式，而涉及到dice距离等特殊聚类（如文本聚类）的以后会单独解释。

sch.linkage(y,method='',metric='',optimal_ordering=False)：系统聚类过程的实际操作函数，其中y为经sch.distance.pdist()计算出的样本间距离矩阵，method为聚类过程中类与类间距离的计算方法，分别有'single'最短距离法，'complete'最长距离法，'average'类平均法，'centroid'重心法，'median'中位数法，'ward'离差平方和法等，具体使用什么方法需要视具体问题而定；

sch.dendrogram(X,labels)：根据上述函数生成的系统聚类过程绘制树状聚类图，X为sch.linkage()计算出的系统聚类过程的相关数据，labels为所有样本未分类前的名称，是一个ndarry型数据，下面基于上面的小例子做一些参数的改变：

name = np.array([chr(i) for i in range(65,75)])#定义样本名称标签
sch.dendrogram(Z,labels=name)#显示树状聚类图
plt.title('Cluster')

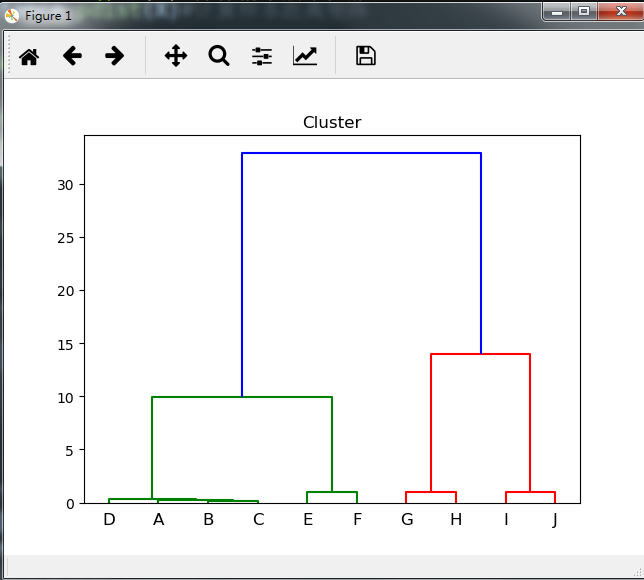
R

在R中进行系统聚类是一种享受，因为其专为统计而生的性质，像这种常规的聚类算法是其自带的，下面介绍在R中进行系统聚类需要的函数:

dist()：用来计算样本间距离矩阵，返回值是R中一种'dist'格式的数据结构，即去除对角和下三角元素后的样本间距离矩阵，其第一个输入值为要计算的样本矩阵，样本X变量形式的矩阵或数据框；另一个常用的参数method用来设置计算距离的方式，包括'euclidean'欧氏距离，'maximum'切比雪夫距离，'manhattan'曼哈顿距离（绝对值距离）,'canberra'兰氏距离

hclust()：用来进行系统聚类的函数，主要输入值有dist形式的样本距离矩阵，类间距离计算方式method,包括了'single'最短距离法，'complete'最长距离法，'average'类平均法，'median'中间距离法，'centroid'重心法，'ward'离差平方和法

而在实际的Q型系统聚类中，变量间存在相关性是很常见的情况，这种时候我们就需要用到马氏距离，很遗憾的是R中计算马氏距离的函数挺傻逼的，并且存在很多不必要的参数需要设定，因此笔者自己根据马氏距离的定义式：[(x-μ)'Σ^(-1)(x-μ)]^(1/2)

通过R中的自建函数编写了一个计算马氏距离dist数据的方便灵活的函数如下以供大家参考：

#自定义马氏距离矩阵计算函数
MS <- function(input){
  l <- length(input[,1])
  ms <- matrix(0,nrow=l,ncol=l)
  cov <- cov(input)
  for(i in 1:l){
    for(j in 1:l){
      ms[i,j] = t(input[i,]-input[j,])%*%solve(cov)%*%(input[i,]-input[j,])
    }
  }
  return(as.dist(ms))
}

其中输入变量为样本矩阵（样本为行，变量为列），输出的结果为dist数据，可直接在hclust()里使用MS(input)来进行聚类。

在通过hclust()完成系统聚类并保存在变量中，只需要用plot()绘制该变量即可画出树状聚类图。