[NOIP2009提高组]靶形数独

题目：洛谷P1074、Vijos P1755、codevs1174。

题目大意：给你一个数独，让你填完这个数独，并要求得分最大，问这个得分是多少（不能填完输出-1）。

每个格子的得分是当前格子所填的数乘格子的分值。

格子的分值如下：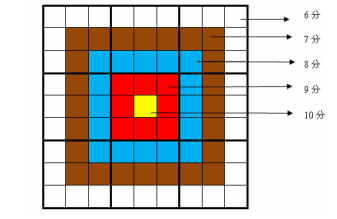

解题思路：暴力搜索。

然而不加优化的搜索是一定会超时的。

我用了这几个优化就过了这道题：

①位运算，用一个九位二进制数来保存每行/列/九宫格中已经用过的数字，则对于一个点，不能用的数字就是它所在行的状态or列的状态or九宫格的状态。

②每次搜索时，找一个能填的数字最少的格子进行搜索。

③register和手动O2(逃

之后只要你不像我一样把求最大值看成最小值，就能AC了。

C++ Code：

#include<cstdio>
using namespace std;
int nin[10][10]={{0},
{0,1,1,1,2,2,2,3,3,3},
{0,1,1,1,2,2,2,3,3,3},
{0,1,1,1,2,2,2,3,3,3},
{0,4,4,4,5,5,5,6,6,6},
{0,4,4,4,5,5,5,6,6,6},
{0,4,4,4,5,5,5,6,6,6},
{0,7,7,7,8,8,8,9,9,9},
{0,7,7,7,8,8,8,9,9,9},
{0,7,7,7,8,8,8,9,9,9}
},sco[10][10]={{0},
{0,6,6,6,6,6,6,6,6,6},
{0,6,7,7,7,7,7,7,7,6},
{0,6,7,8,8,8,8,8,7,6},
{0,6,7,8,9,9,9,8,7,6},
{0,6,7,8,9,10,9,8,7,6},
{0,6,7,8,9,9,9,8,7,6},
{0,6,7,8,8,8,8,8,7,6},
{0,6,7,7,7,7,7,7,7,6},
{0,6,6,6,6,6,6,6,6,6},
};
int sd[10][10],hang[10]={0},lie[10]={0},kuai[10]={0},ans;
__attribute__((optimize("-O2")))void dfs(int s,int p){
	if(p==81){
		if(ans<s)ans=s;
		return;
	}
	int x,y,mn=0x3f3f3f3f;
	for(register int i=1;i<=9;++i){
		for(register int j=1;j<=9;++j)
		if(!sd[i][j]){
			int t=hang[i]|lie[j]|kuai[nin[i][j]],js=0;
			for(register int k=0;k<9;++k)
			js+=!(t&(1<<k));
			if(js<mn)mn=js,x=i,y=j;
			if(js==1)break;
		}
		if(mn==1)break;
	}
	if(mn==0x3f3f3f3f)return;
	int t=hang[x]|lie[y]|kuai[nin[x][y]];
	for(register int k=9;k;--k)
	if(!(t&(1<<(k-1)))){
		int f=1<<(k-1);
		hang[x]^=f;
		lie[y]^=f;
		sd[x][y]=k;
		kuai[nin[x][y]]^=f;
		dfs(s+sco[x][y]*k,p+1);
		hang[x]^=f;
		sd[x][y]=0;
		lie[y]^=f;
		kuai[nin[x][y]]^=f;
	}
}
int main(){
	ans=-1;
	int s=0,p=0;
	for(int i=1;i<=9;++i){
		for(int j=1;j<=9;++j){
			int& now=sd[i][j];
			scanf("%d",&now);
			if(now)s+=now*sco[i][j],++p,hang[i]|=1<<(now-1),lie[j]|=1<<(now-1),kuai[nin[i][j]]|=1<<(now-1);
		}
	}
	dfs(s,p);
	printf("%d\n",ans);
	return 0;
}