2018.2.14 Java中的哈夫曼编码
概念
哈夫曼编码(Huffman Coding),又称霍夫曼编码,是一种编码方式,哈夫曼编码是可变字长编码(VLC)的一种。Huffman于1952年提出一种编码方法,该方法完全依据字符出现概率来构造异字头的平均长度最短的码字,有时称之为最佳编码,一般就叫做Huffman编码(有时也称为霍夫曼编码)。
哈夫曼原理
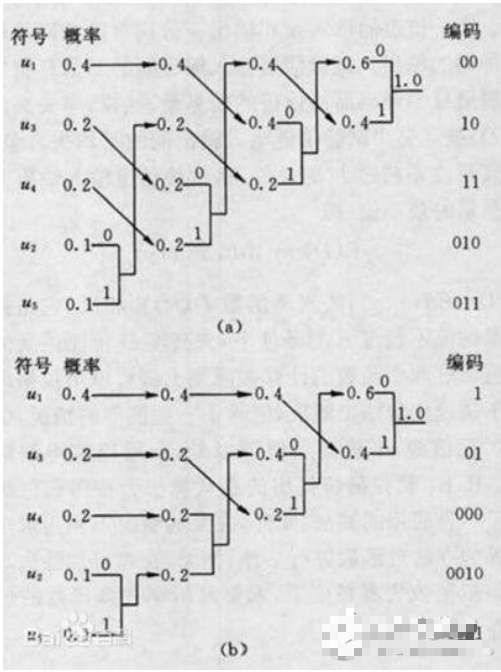
哈夫曼算法流程图
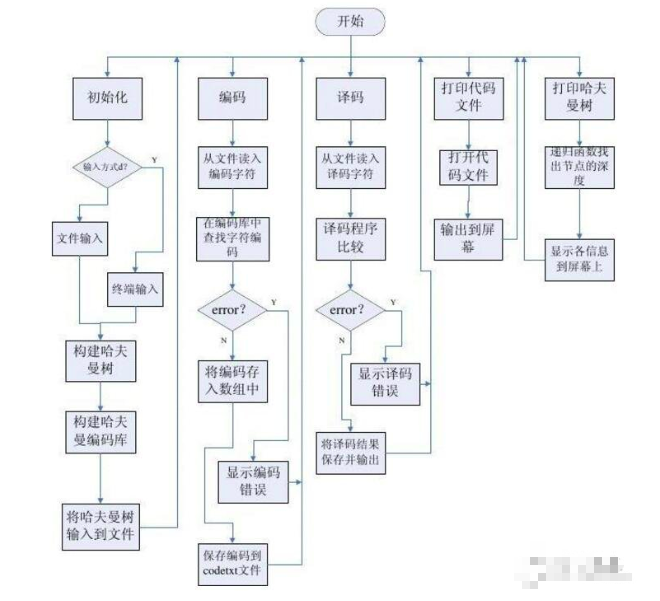
哈夫曼树
给定n个权值作为n个叶子结点,构造一棵二叉树,若带权路径长度达到最小,称这样的二叉树为最优二叉树,也称为哈夫曼树(Huffman Tree)。哈夫曼树是带权路径长度最短的树,权值较大的结点离根较近。
树节点间的边相关的数叫做权。
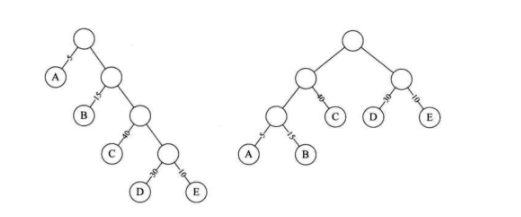
从树中的一个节点到另一个节点之间的分支构成两个点之间的路径,路径上的分支数目称作路径长度。
图中二叉树a中,跟节点到D的路径长度就是4,b中根节点到D的路径长度为2。
树的路径长度就是从树根到每一个节点的路径长度之和。二叉树a的路径长度就为1+1+2+2+3+3+4+4=20。二叉树b的树路径长度就为1+2+3+3+2+1+2+2=16。
如果考虑带权的节点,节点的带权的路径长度就是从该节点到树根之间的路径长度乘该节点的权。
数的带权路径长度就是所有叶子节点的带权路径长度之和。
带权路径长度(WPL)最小的二叉树称作哈夫曼树。
如何构造哈夫曼树
下面我们以【5、8、4、11、9、13】为例来画出哈夫曼树(数字大小代表权重大小,越大的权重越大)
第一步:按从小到大排序。
【5、8、4、11、9、13】→【4、5、8、9、11、13】
第二步:选最小两个数画出一个树,最小数为4和5。
给定的4、5、8、9、11、13为白色, 红色的9为4+5,与给定的白9无关,新序列为:【红9(含子节点4、5)、8、9、11、13】

之后一直重复第一、第二步:排序然后取两个最小值。实际就是一个递归过程
排序:

取两个最小数8和9:
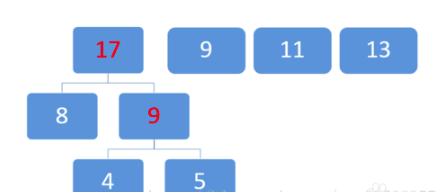
排序
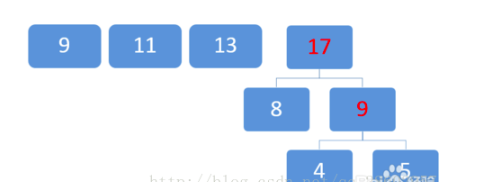
区两个最小数11和9
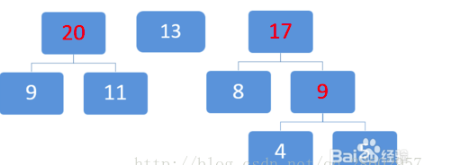
排序,然后取两个最小数13和17:
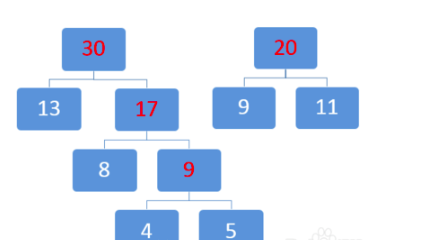
取两个最小数20和30:
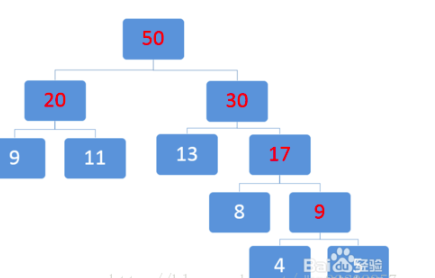
2018.2.14 Java中的哈夫曼编码的更多相关文章
- Java中的哈夫曼树
package com.ietree.basic.datastructure.tree; import java.util.ArrayDeque; import java.util.ArrayList ...
- Java实现哈夫曼编码和解码
最近无意中想到关于api返回值加密的问题,譬如我们的api需要返回一些比较敏感或者重要不想让截获者得到的信息,像如果是做原创图文的,文章明文返回的话则有可能被抓包者窃取. 关于请求时加密的方式比较多, ...
- 10: java数据结构和算法: 构建哈夫曼树, 获取哈夫曼编码, 使用哈夫曼编码原理对文件压缩和解压
最终结果哈夫曼树,如图所示: 直接上代码: public class HuffmanCode { public static void main(String[] args) { //获取哈夫曼树并显 ...
- java使用优先级队列实现哈夫曼编码
思路: 构建小根堆 根据小根堆实现哈夫曼树 根据哈夫曼树对数据进行编码 代码实现如下: /** * @Author: DaleyZou * @Description: 使用java实现一个哈夫曼编码的 ...
- 哈夫曼(huffman)树和哈夫曼编码
哈夫曼树 哈夫曼树也叫最优二叉树(哈夫曼树) 问题:什么是哈夫曼树? 例:将学生的百分制成绩转换为五分制成绩:≥90 分: A,80-89分: B,70-79分: C,60-69分: D,<60 ...
- 哈夫曼(Huffman)树+哈夫曼编码
前天acm实验课,老师教了几种排序,抓的一套题上有一个哈夫曼树的题,正好之前离散数学也讲过哈夫曼树,这里我就结合课本,整理一篇关于哈夫曼树的博客. 主要摘自https://www.cnblogs.co ...
- java实现哈夫曼编码
java实现哈夫曼编码 哈夫曼树 既然是学习哈夫曼编码,我们首先需要知道什么是哈夫曼树:给定n个权值作为n个叶子结点,构造一棵二叉树,若带权路径长度达到最小,称这样的二叉树为最优二叉树,也称为哈夫 ...
- 20172332 2017-2018-2 《程序设计与数据结构》Java哈夫曼编码实验--哈夫曼树的建立,编码与解码
20172332 2017-2018-2 <程序设计与数据结构>Java哈夫曼编码实验--哈夫曼树的建立,编码与解码 哈夫曼树 1.路径和路径长度 在一棵树中,从一个结点往下可以达到的孩子 ...
- word2vec中关于霍夫曼树的
再谈word2vec 标签: word2vec自然语言处理NLP深度学习语言模型 2014-05-28 17:17 16937人阅读 评论(7) 收藏 举报 分类: Felven在职场(86) ...
随机推荐
- python创建矩阵
创建二维数组的办法 直接创建(不推荐) 列表生产式法(可以去列表生成式 - 廖雪峰的官方网站学习) 使用模块numpy创建 举个栗子: 创建一个3*3矩阵,并计算主对角线元素之和. import nu ...
- Codevs 1257 打砖块
1257 打砖块 http://codevs.cn/problem/1257/ 题目描述 Description 在一个凹槽中放置了n层砖块,最上面的一层有n块砖,第二层有n-1块,……最下面一层仅有 ...
- 面试大厂回来后,有一些话想对 Java 后端开发说一说
在上周,我密集面试了若干位Java后端的候选人,工作经验在3到5年间.我的标准其实不复杂:第一能干活,第二Java基础要好,第三最好熟悉些分布式框架,我相信其它公司招初级开发时,应该也照着这个标准来面 ...
- C 语言实例 - 判断字母
C 语言实例 - 判断字母 C 语言实例 C 语言实例 用户输入一个字符,判断该字符是否为一个字母. 实例 #include <stdio.h> int main() { char c; ...
- Exception inside CORBA when accessing a remote bean
http://stackoverflow.com/questions/23291520/exception-inside-corba-when-accessing-a-remote-bean
- php删除文件
unlink() 函数删除文件. 若成功,则返回 true,失败则返回 false. unlink里的参数需要文件的绝对路径
- C# 线程同步计数存在的问题
using System; using System.Collections.Generic; using System.Linq; using System.Text; using System.D ...
- HDU-3639-Hawk-and-Chicken(强连通,缩点,DFS)
链接:https://vjudge.net/problem/HDU-3639 题意: 有n个小朋友在一个班级中,现在要选择班长.收集了小朋友们的意见,一条意见表示为A认为B合适.这个是具备传递性的,A ...
- 2017ACM/ICPC广西邀请赛 Duizi and Shunzi
题意:就是一个集合分开,有两种区分 对子:两个相同数字,顺子:连续三个不同数字,问最多分多少个 解法:贪心,如果当前数字不构成顺子就取对子 /2,如果可以取顺子,那么先取顺子再取对子 #include ...
- 解决git从remote clone后所有文件都改变的问题
遇到2次这种情况了,git从remote clone项目代码后发现所有文件都要改变,因为权限改变了,可以通过git来设置忽略权限变化 git config --global core.fileMode ...
