数学建模python matlab 编程(椭圆声学原理画图证明，解析几何)

证明，在椭圆形的音乐厅内，从一个椭圆的一个焦点发出声音，则另一个焦点听到的声音是最大的。

分析：证明，从椭圆的一个焦点任意发射的直线经过反射后，并经过另一个焦点。

           画图，过一个焦点随机画一条直线l1，再做它与椭圆的交点，过该点作椭圆的一条切线l2，在作一条与该切线垂直的线l3，再作一条l1关于l3对称的直线l4，然后计算另一个焦点到l4的距离小于一个很小的数即可

我的matlab代码

% 画出一个椭圆
t=linspace(0,2*pi,1000);
A=5;
B=4;
C=3;
X=5*cos(t);
Y=4*sin(t);
plot(X,Y),grid on,hold on;
aa=[-3,3]
bb=[0,0]
plot(aa,bb,'o'),hold on;
axis equal

% 随机画出一条直线
k=unifrnd(-10,10);
x0=-3;y0=0;
b=y0-k*x0;
x=-6:6;
y=k*x+b;
plot(x,y),hold on;

% 求椭圆和直线的交点
% （m，n）为切点
syms u v
s=solve(u^2/5^2+v^2/4^2==1,v==k*u+b,u,v)
u=double(s.u)
v=double(s.v)

if u(1)>u(2)
    mx=1
else
    mx=2
end

% 过（m，n）点求切线
% mx/a? + ny/b? =1
kq=-B*B*(u(mx))/(A*A*v(mx))
bq=B*B/v(mx)
x2=-6:6;
y2=kq*x2+bq;
plot(x2,y2),hold on;

% 做一条垂直于切线的线
kq2=-1/kq;
bq2=v(mx)-kq2*u(mx);
y3=kq2*x2+bq2;
plot(x2,y3,'--'),hold on;

% 求出一条直线 关于y3这条直线垂直的直线
% 先找到原直线上任意一点
x0=0
y0=k*x0+b;

% 找到该点关于直线的对称点
A3=kq2;B3=-1;C3=bq2;
x11 = ((B3*B3-A3*A3)*x0-2*A3*B3*y0-2*A3*C3)/(A3*A3+B3*B3)
y11 = ((A3*A3-B3*B3)*y0-2*A3*B3*x0-2*B3*C3)/(A3*A3+B3*B3)
k4=(y11-v(mx))/(x11-u(mx))
b4=v(mx)-k4*u(mx)
x4=-6:6;
y4=k4*x4+b4;
plot(x11,y11,'o'),hold on;
plot(x0,y0,'o'),hold on;
plot(x4,y4),hold on;

% 点到直线y4的距离小于一个很小数
x5=-C;y5=0;
A4=k4;B4=-1;C4=b4;
d = abs(A4*x5+B4*y5+C4)/(sqrt(A4*A4-B4*B4))
d<=0.0000001

再跑个循环，多画几条

% 画出一个椭圆
t=linspace(0,2*pi,1000);
A=5;
B=4;
C=3;
X=5*cos(t);
Y=4*sin(t);
plot(X,Y),grid on,hold on;
aa=[-3,3]
bb=[0,0]
plot(aa,bb,'o'),hold on;
axis equal

for tt=1:5
    % 随机画出一条直线
    k=unifrnd(-10,10);
    x0=-3;y0=0;
    b=y0-k*x0;
    x=-6:6;
    y=k*x+b;
    plot(x,y),hold on;

    % 求椭圆和直线的交点
    % （m，n）为切点
    syms u v
    s=solve(u^2/5^2+v^2/4^2==1,v==k*u+b,u,v)
    u=double(s.u)
    v=double(s.v)

    if u(1)>u(2)
        mx=1
    else
        mx=2
    end

    % 过（m，n）点求切线
    % mx/a? + ny/b? =1
    kq=-B*B*(u(mx))/(A*A*v(mx))
    bq=B*B/v(mx)
    x2=-6:6;
    y2=kq*x2+bq;
    plot(x2,y2),hold on;

    % 做一条垂直于切线的线
    kq2=-1/kq;
    bq2=v(mx)-kq2*u(mx);
    y3=kq2*x2+bq2;
    plot(x2,y3,'--'),hold on;

    % 求出一条直线 关于y3这条直线垂直的直线
    % 先找到原直线上任意一点
    x0=0
    y0=k*x0+b;

    % 找到该点关于直线的对称点
    A3=kq2;B3=-1;C3=bq2;
    x11 = ((B3*B3-A3*A3)*x0-2*A3*B3*y0-2*A3*C3)/(A3*A3+B3*B3)
    y11 = ((A3*A3-B3*B3)*y0-2*A3*B3*x0-2*B3*C3)/(A3*A3+B3*B3)
    k4=(y11-v(mx))/(x11-u(mx))
    b4=v(mx)-k4*u(mx)
    x4=-6:6;
    y4=k4*x4+b4;
    plot(x11,y11,'o'),hold on;
    plot(x0,y0,'o'),hold on;
    plot(x4,y4),hold on;
end

% 点到直线y4的距离小于一个很小数
x5=-C;y5=0;
A4=k4;B4=-1;C4=b4;
d = abs(A4*x5+B4*y5+C4)/(sqrt(A4*A4-B4*B4))
d<=0.0000001

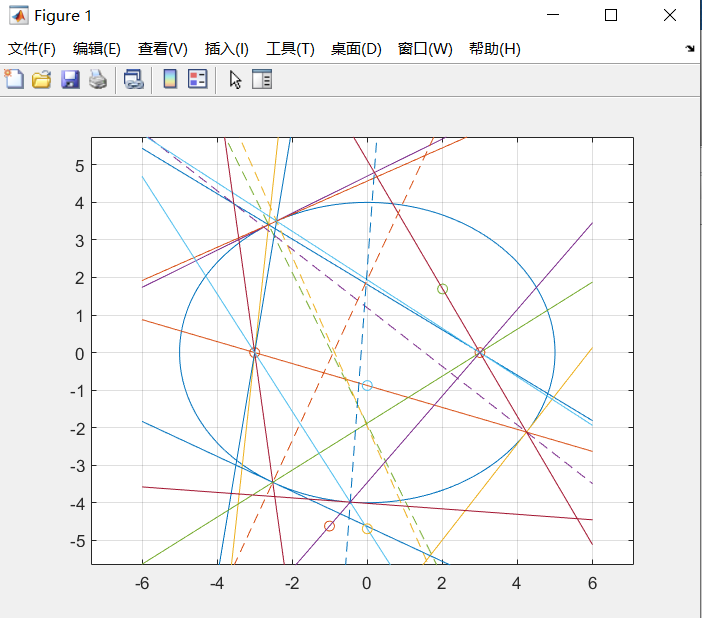
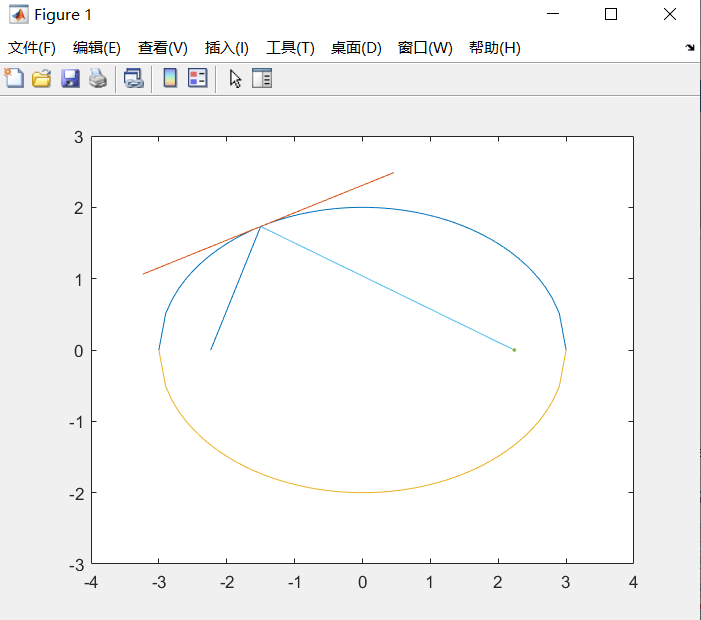
老师的matlab代码

clear;
a=3;b=2;c=sqrt(a^2-b^2);
%f = @(x) x.^2;   %%%%%% 定义函数y=x^2;
f=@(x)b*(1-x.^2.*1/a.^2).^0.5;   %%%%%% 定义函数(x^2)/4+(y^2)/9=1;
x=-1*a:0.1:a;
y=f(x);
x1=-1.5;y1=f(x1);  %确定出切点
k1=-1*(b^2/a^2)*x1/y1;
A1=atan(k1)*180/pi;
plot(x,y);       %画出椭圆的上半段
hold on;

f = @(x) k1*(x-x1)+y1;
x=-1*c-1:0.1:x1+2;
y=f(x);
plot(x,y);
hold on;        %画出切线

f = @(x) -1*b*(1-x.^2.*1/a.^2).^0.5;   %%%%%% 定义函数(x^2)/4+(y^2)/9=1;
x = -1*a:0.1:a;
y = f(x);
plot(x,y);
hold on;        %画出椭圆的下半段

plot(-1*c,0,c,0,'.');     %画出两个焦点
hold on;
line([-1*c,x1],[0,y1]);
hold on; %画出左焦点到切点间的直线

x2=-1*c;y2=0;
k2=(y1-y2)/(x1-x2);
A2=atan(k2)*180/pi;
A3=abs(A2-A1);
A4=A1-A3+180;
B4=A4*pi/180;
k4=tan(B4);

f = @(x) k4*(x-x1)+y1;
x=x1:0.1:c;
y=f(x);
plot(x,y);
hold on;        %画出反射线

axis([-4 4 -3 3])