[译]如何使用Python构建指数平滑模型:Simple Exponential Smoothing, Holt, and Holt-Winters

原文连接：How to Build Exponential Smoothing Models Using Python: Simple Exponential Smoothing, Holt, and…

今年前12个月，iPhone XS将售出多少部?在埃隆·马斯克(Elon musk)在直播节目中吸食大麻之后，特斯拉的需求趋势是什么?这个冬天会暖和吗?(我住在加拿大。)如果你对这些问题感到好奇，指数平滑法可以通过建立模型来预测未来。

指数平滑方法为过去的观测分配指数递减的权重。得到的观测值越近，权重就越大。例如，与12个月前的观测结果相比，对上个月的观测结果给予更大的权重是合理的。

上图为指数平滑权值从过去到现在。

本文将说明如何使用Python和Statsmodel构建简单指数平滑、Holt和Holt- winters模型。对于每个模型，演示都按照以下方式组织。

模型操作方法+Python代码

Statsmodels是一个Python模块，它为实现许多不同的统计模型提供了类和函数。我们需要将它导入Python代码，如下所示。

import matplotlib.pyplot as plt

from statsmodels.tsa.holtwinters import ExponentialSmoothing, SimpleExpSmoothing, Holt

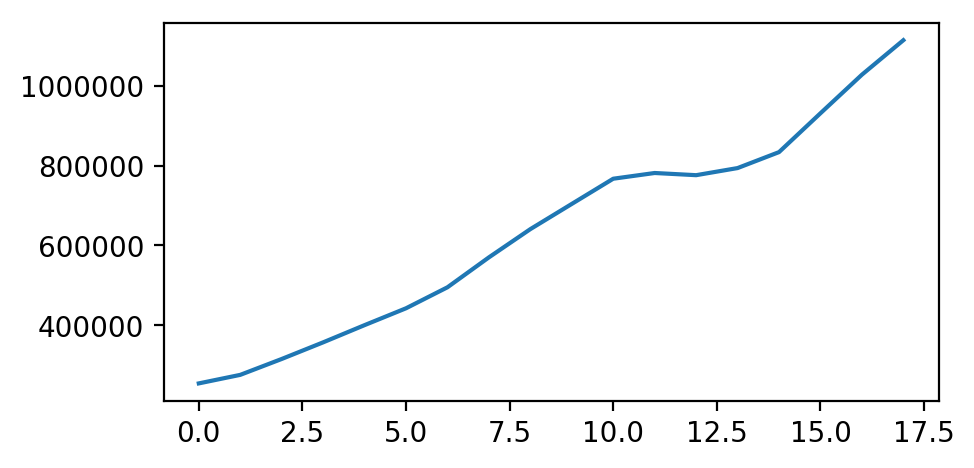
我们示例中的源数据如下：

data = [253993,275396.2,315229.5,356949.6,400158.2,442431.7,495102.9,570164.8,640993.1,704250.4,767455.4,781807.8,776332.3,794161.7,834177.7,931651.5,1028390,1114914]

我们可以先看看折线图

plt.plot(data);

简单指数平滑(SES)

对于没有明显趋势或季节规律的预测数据，SES是一个很好的选择。预测是使用加权平均来计算的，这意味着最大的权重与最近的观测值相关，而最小的权重与最远的观测值相关

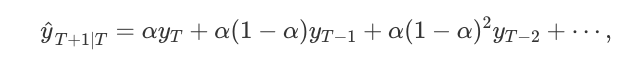
其中0≤α≤1是平滑参数。

权重减小率由平滑参数α控制。如果α很大（即接近1），则对更近期的观察给予更多权重。有两种极端情况：

α= 0：所有未来值的预测等于历史数据的平均值（或“平均值”），称为平均值法。
α= 1：简单地将所有预测设置为最后一次观测的值，统计中称为朴素方法。

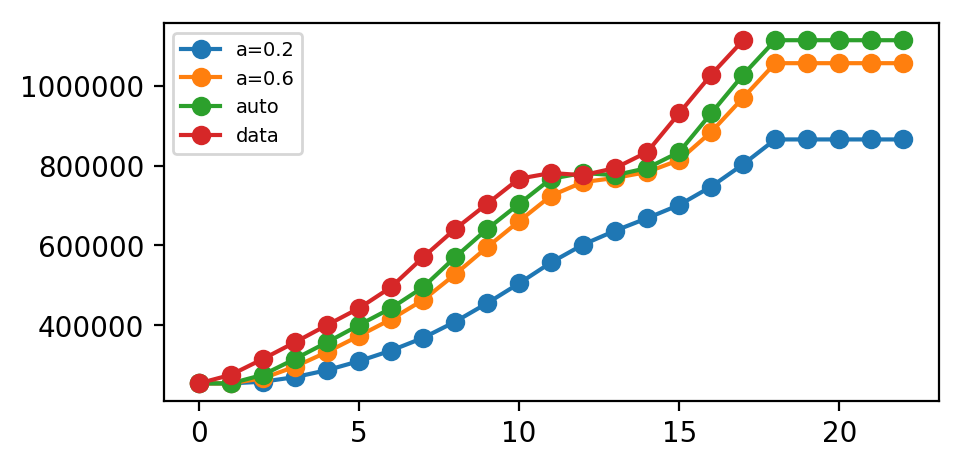
这里我们运行三种简单指数平滑变体：

在fit1中，我们明确地为模型提供了平滑参数$α= 0.2$
在fit2中，我们选择$α= 0.6$
在fit3中，我们使用自动优化，允许statsmodels自动为我们找到优化值。 这是推荐的方法。

# Simple Exponential Smoothing

fit1 = SimpleExpSmoothing(data).fit(smoothing_level=0.2,optimized=False)

# plot

l1, = plt.plot(list(fit1.fittedvalues) + list(fit1.forecast(5)), marker='o')

fit2 = SimpleExpSmoothing(data).fit(smoothing_level=0.6,optimized=False)

# plot

l2, = plt.plot(list(fit2.fittedvalues) + list(fit2.forecast(5)), marker='o')

fit3 = SimpleExpSmoothing(data).fit()

# plot

l3, = plt.plot(list(fit3.fittedvalues) + list(fit3.forecast(5)), marker='o')

l4, = plt.plot(data, marker='o')

plt.legend(handles = [l1, l2, l3, l4], labels = ['a=0.2', 'a=0.6', 'auto', 'data'], loc = 'best', prop={'size': 7})

plt.show()

我们预测了未来五个点。

Holt's 方法(二次指数平滑)

Holt扩展了简单的指数平滑（数据解决方案没有明确的趋势或季节性），以便在1957年预测数据趋势.Holt的方法包括预测方程和两个平滑方程（一个用于水平，一个用于趋势）：

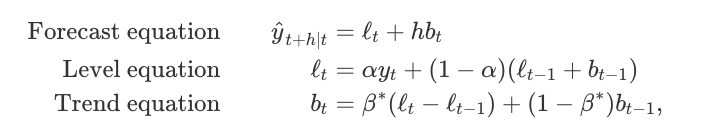
其中$0≤α≤1$是水平平滑参数，$0≤β*≤1$是趋势平滑参数。

对于长期预测，使用Holt方法的预测在未来会无限期地增加或减少。在这种情况下，我们使用具有阻尼参数$0 <φ<1$的阻尼趋势方法来防止预测“失控”。

同样，这里我们运行Halt方法的三种变体：

在fit1中，我们明确地为模型提供了平滑参数$α= 0.8$，$β* = 0.2$。
在fit2中，我们使用指数模型而不是Holt的加法模型（默认值）。
在fit3中，我们使用阻尼版本的Holt附加模型，但允许优化阻尼参数$φ$，同时固定$α= 0.8$，$β* = 0.2$的值。

data_sr = pd.Series(data)

# Holt’s Method

fit1 = Holt(data_sr).fit(smoothing_level=0.8, smoothing_slope=0.2, optimized=False)

l1, = plt.plot(list(fit1.fittedvalues) + list(fit1.forecast(5)), marker='^')

fit2 = Holt(data_sr, exponential=True).fit(smoothing_level=0.8, smoothing_slope=0.2, optimized=False)

l2, = plt.plot(list(fit2.fittedvalues) + list(fit2.forecast(5)), marker='.')

fit3 = Holt(data_sr, damped=True).fit(smoothing_level=0.8, smoothing_slope=0.2)

l3, = plt.plot(list(fit3.fittedvalues) + list(fit3.forecast(5)), marker='.')

l4, = plt.plot(data_sr, marker='.')

plt.legend(handles = [l1, l2, l3, l4], labels = ["Holt's linear trend", "Exponential trend", "Additive damped trend", 'data'], loc = 'best', prop={'size': 7})

plt.show()

Holt-Winters 方法(三次指数平滑)

(彼得·温特斯(Peter Winters)是霍尔特(Holt)的学生。霍尔特-温特斯法最初是由彼得提出的，后来他们一起研究。多么美好而伟大的结合啊。就像柏拉图遇到苏格拉底一样。)

Holt-Winters的方法适用于具有趋势和季节性的数据，其包括季节性平滑参数$γ$。此方法有两种变体：

加法方法：整个序列的季节变化基本保持不变。
乘法方法：季节变化与系列水平成比例变化。

在这里，我们运行完整的Holt-Winters方法，包括趋势组件和季节性组件。 Statsmodels允许所有组合，包括如下面的示例所示：

在fit1中，我们使用加法趋势，周期season_length = 4的加性季节和Box-Cox变换。
在fit2中，我们使用加法趋势，周期season_length = 4的乘法季节和Box-Cox变换。
在fit3中，我们使用加性阻尼趋势，周期season_length = 4的加性季节和Box-Cox变换。
在fit4中，我们使用加性阻尼趋势，周期season_length = 4的乘法季节和Box-Cox变换。

data_sr = pd.Series(data)

fit1 = ExponentialSmoothing(data_sr, seasonal_periods=4, trend='add', seasonal='add').fit(use_boxcox=True)

fit2 = ExponentialSmoothing(data_sr, seasonal_periods=4, trend='add', seasonal='mul').fit(use_boxcox=True)

fit3 = ExponentialSmoothing(data_sr, seasonal_periods=4, trend='add', seasonal='add', damped=True).fit(use_boxcox=True)

fit4 = ExponentialSmoothing(data_sr, seasonal_periods=4, trend='add', seasonal='mul', damped=True).fit(use_boxcox=True)

l1, = plt.plot(list(fit1.fittedvalues) + list(fit1.forecast(5)), marker='^')

l2, = plt.plot(list(fit2.fittedvalues) + list(fit2.forecast(5)), marker='*')

l3, = plt.plot(list(fit3.fittedvalues) + list(fit3.forecast(5)), marker='.')

l4, = plt.plot(list(fit4.fittedvalues) + list(fit4.forecast(5)), marker='.')

l5, = plt.plot(data, marker='.')

plt.legend(handles = [l1, l2, l3, l4, l5], labels = ["aa", "am", "aa damped", "am damped","data"], loc = 'best', prop={'size': 7})

plt.show()

总而言之，我们通过3个指数平滑模型的机制和python代码。如下表所示，我提供了一种为数据集选择合适模型的方法。

总结了指数平滑方法中不同分量形式的平滑参数。

指数平滑是当今行业中应用最广泛、最成功的预测方法之一。如何预测零售额、游客数量、电力需求或收入增长？指数平滑是你需要展现未来的超能力之一。