zoj 4122 Triangle City 2019山东省赛J题

题目链接

题意：

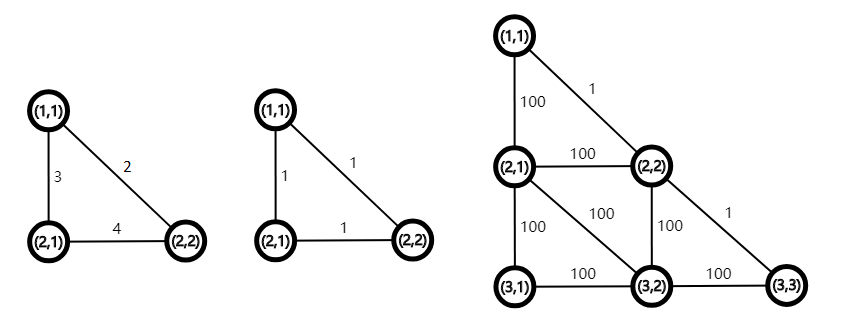
给出一个无向图，类似三角形的样子，然后给出边的权值，问找一条从第一个点到最后一个点的路径，要求每一条边只能走一次，并且权值和最大，点可以重复走。

思路：

首先观察这个图可以发现，所有的点的度数都是偶数。然后由每条边只能走一次知道，这个是和欧拉路相关的，是欧拉道路，不是欧拉回路，因为题目要求是从一个点到另一个点。但是图的所有点的度数都是偶数，那么想办法让图中的第一个点和最后一个点度数变为奇数，其他点的度数都是偶数。这个就比较巧妙，去掉从第一个点到最后一个点的一条无重复点的路径，除了起点和终点度数减1，其它点的度数都减2，目的就达到了。由于题目要求最后走的边的权值和最大，所以去掉的边的权值尽量小，那么从起点到终点求一个最短路即可。

求路径的方法是首先标记最短路上的边，然后从起点或终点开始dfs，走过的每条边标记（注意这是无向图，所以反向路径也要标记），当一个点再无边可走的时候，就把它放入路径中，这样可以保证求出的一定是一个欧拉道路。

代码：

#include <stdio.h>
#include <string.h>
#include <algorithm>
#include <vector>
#include <queue>
using namespace std;
typedef long long ll;
typedef pair<int,int> pii;
const int N = 305;
const int inf = 0x3f3f3f3f;

struct edge
{
	int u,v,cost;
	edge(int u,int v,int cost):u(u),v(v),cost(cost){}
	edge(){}
};

int a[N][N],b[N][N],c[N][N];
int mp[N][N];

vector<edge> es;
vector<int> G[N*N];
vector<pii> anc;

void adde(int u,int v,int cost)
{
	es.push_back(edge(u,v,cost));
	es.push_back(edge(v,u,cost));
	int sz = es.size();
	G[u].push_back(sz-2);
	G[v].push_back(sz-1);
}

ll dis[N*N];
int rev[N*N];
bool vis[N*N];
bool used[N*N*8];
pii rid[N*N];

int cnt;

void spfa()
{
	for (int i = 0;i <= cnt;i++) dis[i] = 1e18;
	memset(vis,0,sizeof(vis));
	memset(rev,0,sizeof(rev));
	vis[1] = 1;
	dis[1] = 0;
	queue<int> q;
	q.push(1);
	while (!q.empty())
	{
		int u = q.front();
		q.pop();
		vis[u] = 0;
		for (int i = 0;i < G[u].size();i++)
		{
			edge &e = es[G[u][i]];
			int v = e.v;
			if (dis[v] > dis[u] + e.cost)
			{
				dis[v] = dis[u] + e.cost;
				rev[v] = G[u][i];
				if (!vis[v])
				{
					vis[v] = 1;
					q.push(v);
				}
			}
		}
	}
}

void dfs(int u)
{
	for (int i = 0;i < G[u].size();i++)
	{
		int id = G[u][i];
		edge &e = es[id];
		if (!used[id])
		{
			used[id] = used[id^1] = 1;
			int v = e.v;
			dfs(v);
		}
	}
	anc.push_back(rid[u]);
}

void init()
{
	cnt = 0;
	anc.clear();
	es.clear();
	for (int i = 0;i < N * N;i++) G[i].clear();
}

int main()
{
	int t;
	scanf("%d",&t);
	while (t--)
	{
		int n;
		scanf("%d",&n);
		init();
		ll ans = 0;
		for (int i = 1;i < n;i++)
		{
			for (int j = 1;j <= i;j++)
			{
				scanf("%d",&a[i][j]);
				ans += a[i][j];
			}
		}
		for (int i = 1;i < n;i++)
		{
			for (int j = 1;j <= i;j++)
			{
				scanf("%d",&b[i][j]);
				ans += b[i][j];
			}
		}
		for (int i = 1;i < n;i++)
		{
			for (int j = 1;j <= i;j++)
			{
				scanf("%d",&c[i][j]);
				ans += c[i][j];
			}
		}

		for (int i = 1;i <= n;i++)
		{
			for (int j = 1;j <= i;j++)
			{
				mp[i][j] = ++cnt;
				rid[cnt] = pii(i,j);
			}
		}
		for (int i = 1;i < n;i++)
		{
			for (int j = 1;j <= i;j++)
			{
				int x = mp[i][j];
				int y = mp[i+1][j];
				adde(x,y,a[i][j]);
				y = mp[i+1][j+1];
				adde(x,y,b[i][j]);
				x = mp[i+1][j];
				y = mp[i+1][j+1];
				adde(x,y,c[i][j]);
			}
		}
		spfa();
		ans -= dis[cnt];
		memset(used,0,sizeof(used));
		for (int i = cnt;i != 1;i = es[rev[i]].u)
		{
			used[rev[i]] = used[rev[i]^1] = 1;
		}
		dfs(cnt);
		printf("%lld\n",ans);
		printf("%d\n",(int)anc.size());
		for (int i = 0;i < anc.size();i++)
		{
			printf("%d %d%c",anc[i].first,anc[i].second,i == anc.size() - 1 ? '\n' : ' ');
		}
	}
	return 0;
}