canvas 2d 贴图技术实践

　　最近在公司内部的技术协会论坛里闲逛的时候，无意中发现了一篇手淘前端大牛岑安两年前写的博文，讲述了canvas的2d贴图技术。看到后觉得相当神奇。于是就自己实现了一下。不过岑安前辈的那篇博文也只是大概讲述了一下实现思路，整个逻辑还是自己慢慢摸索出来的，过程还是挺心酸的，所以在此记录一下并且分享一下，让跟我一样喜欢canvas的人有所收获吧。

　　废话不说，先把demo贴出来，好歹让大伙看看我们要实现怎样的效果：

　　第一个demo： 图像拉扯变形demo_1

　　第二个demo： 图像3d变形demo_2

　　看完demo，是否觉得挺好玩的？

　　如果觉得好玩，那就继续看下去吧，接下来我将逐步分析整个实现逻辑。主要讲的就是第一个demo的实现逻辑，因为第二个就是在第一个的基础上实现的，只要理解了第一个的原理，第二个就变得很简单了。

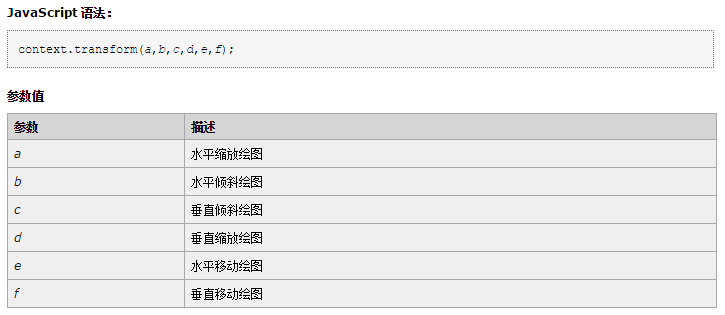
　　第一个demo中，实现了对图像的拉扯，涉及到这种变形的，首先想到的就是transform，没错，就是canvas的2d绘图API中的transform啦。transform方法中传入的abcdef六个值就是变换矩阵的参数。也就是说，我们可以通过修改这六个值来实现对图片的变形操作。

　　transform() 允许您缩放、旋转、移动并倾斜当前的环境。如果对transform不是很了解的，可以看这篇博文：http://yehao.diandian.com/post/2012-12-30/40046242001    里面讲的还是很详细的。

　　

　　了解了transform之后，你会发现，transform能做的，好像就只有缩放、旋转、移动、倾斜这几个功能。但是demo1中可以拉扯成各种形状，感觉不像是用这几个就能实现的。但是其实，还真就是用这几个变换实现的。

　　demo1贴图右侧有个数值选择，当选择1，并且选择显示方框的时候，我们看到是这样一个画面：

　　

　　没错，这个是什么意思呢，说明这张图片其实分成了两块，左上角的三角形以及右下角的三角形，我们拖动一下图片，再看一下效果：

　　

　　为了方便理解，我加了辅助线，画了辅助线后，就变得很简单了，相当于分成了两块，上面正常的图片，一块是变成了由红色圈起来的，另一块则是变成了由黑色圈起来的，当用画笔补全后，两个三角形都其实是一个平行四边形，而从矩形变成平行四边形，transform就能做了，当变成我们需要的形状的时候，再通过canvas的clip方法，只截取一半的三角形，把两块三角形合并起来。就有了拉扯效果了。

　　而为了让拉扯效果更真实，就自然就需要使用更多的三角区域，当我把矩形分成20*20个小矩形，也就是20*20*2个三角形的时候，当鼠标拉扯时就出现了以下效果：

　　

　　以上，就是demo1的整个理论逻辑。

　　接下来就讲代码该如何实现：

　　首先是图片的变形效果，也就是用transform，要传入矩阵参数，起初我是用向量来做的，但是做到后面发现向量做起来会有好多其他问题。比如：图片拉扯过度的时候，图片翻转就出问题了，等等。。。

　　所以最后，还是选择了用代数法来实现，也就是要解三元一次方程！！！！

　　为啥说是三元一次方程呢？因为按照transform的矩阵运算的规则

　　　　　　　　　　　　    |a , b , 0|

　　[X,Y,1] = [x , y , 1] * |c , d , 0|

　　　　　　　　　　　　|e , f , 1|

　　解出来就是这样：X = ax + cy +e  和  Y = bx + dy + f  ， 也就是，新的坐标的XY值就等于旧的坐标的xy值进行一些运算后可以得到。

　　相对的，也就是说，只要我们知道了平行四边形三个顶点变换前后的坐标值，我们就可以算出abcdef六个矩阵参数，然后我们先用transform改变绘制环境，再把图片绘制到平行四边形变换前的位置，就可以绘制出相应的倾斜效果了。

　　所以，首先我们要封装出一个解三元一次方程以及获取矩阵参数的方法：

　　先是解三元一次方程的方法，具体原理我就不讲了，百度一下就知道了，或者有琢磨精神的可以自己亲自拿笔算一下：

/**
     * 解三元一次方程，需要传入三组方程参数
     * @param arr1        第一组参数
     * @param arr2        第二组参数
     * @param arr3        第三组参数
     * @returns {{x: number, y: number, z: number}}
     */
    function equation(arr1 , arr2 , arr3){
        var a1 = +arr1[0];
        var b1 = +arr1[1];
        var c1 = +arr1[2];
        var d1 = +arr1[3];

        var a2 = +arr2[0];
        var b2 = +arr2[1];
        var c2 = +arr2[2];
        var d2 = +arr2[3];

        var a3 = +arr3[0];
        var b3 = +arr3[1];
        var c3 = +arr3[2];
        var d3 = +arr3[3];

        //分离计算单元
        var m1 = c1 - (b1 * c2 / b2);
        var m2 = c2 - (b2 * c3 / b3);
        var m3 = d2 - (b2 * d3 / b3);
        var m4 = a2 - (b2 * a3 / b3);
        var m5 = d1 - (b1 * d2 / b2);
        var m6 = a1 - (b1 * a2 / b2);

        //计算xyz
        var x = ((m1 / m2) * m3 - m5)/((m1 / m2) * m4 - m6);
        var z = (m3 - m4 * x) / m2;
        var y = (d1 - a1 * x - c1 * z) / b1;

        return {
            x : x,
            y : y,
            z : z
        }
    }

　　然后就是获取矩阵，其实就是将各个参数整理一下，传入解方程的方法中，进行处理：　

/**
     * 根据变化前后的点坐标，计算矩阵
     * @param arg_1     变化前坐标1
     * @param _arg_1    变化后坐标1
     * @param arg_2     变化前坐标2
     * @param _arg_2    变化后坐标2
     * @param arg_3     变化前坐标3
     * @param _arg_3    变化后坐标3
     * @returns {{a: number, b: number, c: number, d: number, e: number, f: number}}
     */
    function getMatrix(arg_1 , _arg_1 , arg_2 , _arg_2 , arg_3 , _arg_3){
        //传入x值解第一个方程 即  X = ax + cy + e 求ace
        //传入的四个参数，对应三元一次方程：ax+by+cz=d的四个参数：a、b、c、d，跟矩阵方程对比c为1
        var arr1 = [arg_1.x , arg_1.y , 1 , _arg_1.x];
        var arr2 = [arg_2.x , arg_2.y , 1 , _arg_2.x];
        var arr3 = [arg_3.x , arg_3.y , 1 , _arg_3.x];

        var result = equation(arr1 , arr2 , arr3);

        //传入y值解第二个方程 即  Y = bx + dy + f 求 bdf
        arr1[3] = _arg_1.y;
        arr2[3] = _arg_2.y;
        arr3[3] = _arg_3.y;

        var result2 = equation(arr1 , arr2 , arr3);

        //获得a、c、e
        var a = result.x;
        var c = result.y;
        var e = result.z;

        //获得b、d、f
        var b = result2.x;
        var d = result2.y;
        var f = result2.z;

        return {
            a : a,
            b : b,
            c : c,
            d : d,
            e : e,
            f : f
        };
    }

　　计算完毕，就可以获取到六个矩阵参数了。

　　这两个计算看似简单，但是一不小心就容易出错，楼主之前做的时候就一直出错，一直不知道原因在哪，最后手动把三元一次方程解了一遍，才发现是某个参数错了。所以楼主把这两个计算封装了一下，以便以后再利用：

　　github地址：https://github.com/whxaxes/wheels/tree/master/matrix 　　有兴趣或者有需要的可以一用

　　回归正题，到了现在，我们就可以获取到所有的矩阵参数了，接下来要解决的问题，就是如何把任意四个点连线形成的四边形分成N份的逻辑了（注意：是任意四个点，因为拉升之后，四个点形成的坐标就不是矩形了）。这个就可以用向量来做了，用向量的话，计算量会小很多，对性能的提升也是很有帮助。

　　怎么实现呢，画个图就清晰了：

　　

　　我们只需要获取到AD向量，以及BC向量，把两个向量N等分，然后用个循环，在每一等分上获取AB方向的向量，然后再进行N等分，再计算，就可以获取到所有的点了。因为用的是向量，所以我们完全不用考虑角度的问题，无论四边形的形状如何，只要我们有四个点的坐标，就可以计算出里面的所有点坐标。代码如下：

/**
     * 将abcd四边形分割成n的n次方份，获取n等分后的所有点坐标
     * @param n     多少等分
     * @param a     a点坐标
     * @param b     b点坐标
     * @param c     c点坐标
     * @param d     d点坐标
     * @returns {Array}
     */
    function rectsplit(n , a , b , c , d){
        //ad向量方向n等分
        var ad_x = (d.x - a.x)/n;
        var ad_y = (d.y - a.y)/n;
        //bc向量方向n等分
        var bc_x = (c.x - b.x)/n;
        var bc_y = (c.y - b.y)/n;

        var ndots = [];
        var x1, y1, x2, y2, ab_x, ab_y;

        //左边点递增，右边点递增，获取每一次递增后的新的向量，继续n等分，从而获取所有点坐标
        for(var i=0;i<=n;i++){
            //获得ad向量n等分后的坐标
            x1 = a.x + ad_x * i;
            y1 = a.y + ad_y * i;
            //获得bc向量n等分后的坐标
            x2 = b.x + bc_x * i;
            y2 = b.y + bc_y * i;

            for(var j=0;j<=n;j++){
                //ab向量为：[x2 - x1 , y2 - y1]，所以n等分后的增量为除于n
                ab_x = (x2 - x1)/n;
                ab_y = (y2 - y1)/n;

                ndots.push({
                    x: x1 + ab_x * j,
                    y: y1 + ab_y * j
                })
            }
        }

        return ndots;
    }

　　计算完毕，并且把点绘制到各个坐标上的时候，拖动四个顶点，就出现了以下效果，无论我的四个顶点位置如何变幻，都能保证所有点的位置不会错。

　　

　　当这个也计算完毕，整个demo的制作就基本上完成了，然后就是进行图片的渲染了，接下来的逻辑就相当简单了，先是用上面的rectsplit方法把当前的四边形分成N份，并且获取所有坐标点，当然还需要直接获取初始四边形分成N份后的所有坐标点，不过这个是可以在刚开始的时候就初始化好，因为这个数值是不会变的，没必要重复计算。

　　两组点坐标获取到，然后传入方法里计算矩阵，以及进行clip处理，再把图片绘制上去，整个渲染过程就完成了。

/**
     * 画布渲染
     */
    function render(){
        ctx.clearRect(0,0,canvas.width,canvas.height);

        var ndots = rectsplit(count, dots[0], dots[1], dots[2], dots[3]);

        ndots.forEach(function(d , i){
            //获取四边形的四个点
            var dot1 = ndots[i];
            var dot2 = ndots[i + 1];
            var dot3 = ndots[i + count + 2];
            var dot4 = ndots[i + count + 1];

            //获取初始四边形的四个点
            var idot1 = idots[i];
            var idot2 = idots[i + 1];
            var idot3 = idots[i + count + 2];
            var idot4 = idots[i + count + 1];

            if (dot2 && dot3 && i%(count+1)<count){
                //绘制三角形的下半部分
                renderImage(idot3, dot3, idot2, dot2, idot4, dot4);

                //绘制三角形的上半部分
                renderImage(idot1, dot1, idot2, dot2, idot4, dot4);
            }

            if(hasDot){
                ctx.save();
                ctx.fillStyle = "red";
                ctx.fillRect(d.x-1 , d.y-1 , 2 , 2);
                ctx.save();
            }
        });
    }

    /**
     * 计算矩阵，同时渲染图片
     * @param arg_1
     * @param _arg_1
     * @param arg_2
     * @param _arg_2
     * @param arg_3
     * @param _arg_3
     */
    function renderImage(arg_1 , _arg_1 , arg_2 , _arg_2 , arg_3 , _arg_3){
        ctx.save();
        //根据变换后的坐标创建剪切区域
        ctx.beginPath();
        ctx.moveTo(_arg_1.x, _arg_1.y);
        ctx.lineTo(_arg_2.x, _arg_2.y);
        ctx.lineTo(_arg_3.x, _arg_3.y);
        ctx.closePath();
        if(hasRect){
            ctx.lineWidth = 2;
            ctx.strokeStyle = "red";
            ctx.stroke();
        }
        ctx.clip();

        if(hasPic){
            //传入变换前后的点坐标，计算变换矩阵
            var result = matrix.getMatrix.apply(this , arguments);

            //变形
            ctx.transform(result.a , result.b , result.c , result.d , result.e , result.f);

            //绘制图片
            ctx.drawImage(img , idots[0].x , idots[0].y , img.width , img.height);
        }

        ctx.restore();
    }

　　

　　至此，demo1的整个理论原理以及代码逻辑都分析完毕，下面贴出该项目的github地址：

　　https://github.com/whxaxes/canvas-test/tree/gh-pages/src/Funny-demo/transform　　

　　

　　当demo1做出来的时候，demo2也就很简单了，因为，只要我们知道四边形的各个点变换前后的坐标值，我们就可以让图片变形成任何我们想要的样子。

　　而上面的demo2就是在demo1的基础上，加入了z轴的影响，x，y轴都仅仅是平面上的，当加入了z轴以后，再将z轴的值映射到x，y轴上来，然后再进行图片变换，就有了demo2的效果。demo2的源码也在上面那个github地址上，里面的demo1.js就是demo1的，demo2.js就是demo2的逻辑。

　　

　　至此，整个过程都讲述完了。感谢一阅。