P3381 【模板】最小费用最大流

P3381 【模板】最小费用最大流

题目描述

如题，给出一个网络图，以及其源点和汇点，每条边已知其最大流量和单位流量费用，求出其网络最大流和在最大流情况下的最小费用。

输入输出格式

输入格式：

第一行包含四个正整数N、M、S、T，分别表示点的个数、有向边的个数、源点序号、汇点序号。

接下来M行每行包含四个正整数ui、vi、wi、fi，表示第i条有向边从ui出发，到达vi，边权为wi（即该边最大流量为wi），单位流量的费用为fi。

输出格式：

一行，包含两个整数，依次为最大流量和在最大流量情况下的最小费用。

输入输出样例

输入样例#1：

4 5 4 3
4 2 30 2
4 3 20 3
2 3 20 1
2 1 30 9
1 3 40 5

输出样例#1：

50 280

说明

时空限制：1000ms,128M

数据规模：

对于30%的数据：N<=10，M<=10

对于70%的数据：N<=1000，M<=1000

对于100%的数据：N<=5000，M<=50000

样例说明：

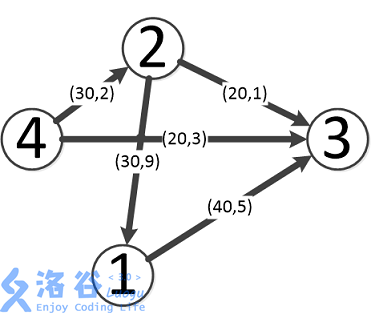
如图，最优方案如下：

第一条流为4-->3，流量为20，费用为3*20=60。

第二条流为4-->2-->3，流量为20，费用为（2+1）*20=60。

第三条流为4-->2-->1-->3，流量为10，费用为（2+9+5）*10=160。

故最大流量为50，在此状况下最小费用为60+60+160=280。

故输出50 280。

90分的MCMF（dijkstra被卡常数了）

#include<cstdio>
#include<cstring>
#include<queue>
#define pir pair<int,int>
#define inf 0x33333333
using namespace std;
const int N=1e4+;
const int M=1e5+;
struct node{
    int v,next,cap,cost;
    node(int v=,int next=,int cap=,int cost=):v(v),next(next),cap(cap),cost(cost){}
}e[M<<];int tot=;
int n,m,S,T,head[N],pv[N],pe[N],dis[N],h[N];
bool vis[N];
void add(int x,int y,int cap,int cost){
    e[++tot]=node(y,head[x],cap,cost);
    head[x]=tot;
}
pir MCMF(){
    int flow=,cost=;
    while(){
        memset(dis,0x33,sizeof dis);
        priority_queue<pir,vector<pir>,greater<pir> >q;
        q.push(make_pair(dis[S]=,S));
        while(!q.empty()){
            pir t=q.top();q.pop();
            int x=t.second;
            if(t.first!=dis[x]) continue;
            if(x==T) break;
            for(int i=head[x];i;i=e[i].next){
                int v=e[i].v,newcost=e[i].cost+h[x]-h[v];
                if(e[i].cap>&&dis[v]>dis[x]+newcost){
                    dis[v]=dis[x]+newcost;
                    q.push(make_pair(dis[v],v));
                    pv[v]=x;pe[v]=i;
                }
            }
        }
        if(dis[T]==inf) break;
        for(int i=;i<=n;i++) h[i]=min(h[i]+dis[i],inf);
        int newflow=inf;
        for(int i=T;i!=S;i=pv[i]){
            newflow=min(newflow,e[pe[i]].cap);
        }
        flow+=newflow;
        cost+=newflow*h[T];
        for(int i=T;i!=S;i=pv[i]){
            e[pe[i]].cap-=newflow;
            e[pe[i]^].cap+=newflow;
        }
    }
    return make_pair(flow,cost);
}
int main(){
    scanf("%d%d%d%d",&n,&m,&S,&T);
    for(int i=,x,y,z,w;i<=m;i++) scanf("%d%d%d%d",&x,&y,&z,&w),add(x,y,z,w),add(y,x,,-w);
    pir ans=MCMF();
    printf("%d %d",ans.first,ans.second);
    return ;
}

100分(改成spfa就过了)

/*
以费用作为权值，求出最小费用链，然后在这条链上求得一个最小流量，直到找不到费用链。求最小费用链也就相当于求src->des的最短路径。
使用spfa+EK算法。得到MCMF算法
*/

#include<cstdio>
#include<cstring>
#include<iostream>
#define inf 0x7fffffff
using namespace std;
const int N=1e4+;
const int M=1e5+;
struct node{
    int v,next,cap,cost;
}e[M*];int tot=;
int n,m,S,T,head[N],dis[N],flow[N],pree[N],q[M*];
int Flow,Cost;
bool vis[N];
void add(int x,int y,int a,int b){
    e[++tot].v=y;e[tot].cap=a;e[tot].cost=b;e[tot].next=head[x];head[x]=tot;
    e[++tot].v=x;e[tot].cap=;e[tot].cost=-b;e[tot].next=head[y];head[y]=tot;
}
bool spfa(){
    for(int i=;i<=n;i++) vis[i]=,dis[i]=inf;
    int h=,t=;dis[S]=;q[t]=S;flow[S]=inf;pree[S]=;
    while(h!=t){
        int x=q[++h];vis[x]=;
        for(int i=head[x];i;i=e[i].next){
            int v=e[i].v;
            if(e[i].cap&&dis[v]>dis[x]+e[i].cost){
                dis[v]=dis[x]+e[i].cost;
                pree[v]=i;
                flow[v]=min(flow[x],e[i].cap);
                if(!vis[v]){
                    vis[v]=;
                    q[++t]=v;
                }
            }
        }
    }
    return dis[T]<inf;
}
void agument(){
    for(int i=T;i!=S;i=e[pree[i]^].v){
        e[pree[i]].cap-=flow[T];
        e[pree[i]^].cap+=flow[T];
    }
    Flow+=flow[T];
    Cost+=flow[T]*dis[T];
}
void MCMF(){
    while(spfa()) agument();
}
int main(){
    scanf("%d%d%d%d",&n,&m,&S,&T);
    for(int i=,x,y,z,w;i<=m;i++) scanf("%d%d%d%d",&x,&y,&z,&w),add(x,y,z,w);
    MCMF();
    printf("%d %d\n",Flow,Cost);
    return ;
}