Solution -「多校联训」战神归来

\(\mathcal{Description}\)

  Link.

  一条地铁线路上共 \(m\) 个站点，\(n\) 个人乘坐地铁，第 \(i\) 个人需要从 \(s_i\) 站坐到 \(e_i\) 站。你可以指挥他们在保证不走回头路的情况下走到某个站，或指挥处于同一个站的两人交换地铁卡。一张从 \(x\) 站进站 \(y\) 站出站的地铁卡花费为 \(|x-y|\)，最小化花费和并给出可行方案。

  \(n\le10^5\)，\(m\le10^6\)，方案步骤数 \(\le 4\times10^5\)。

\(\mathcal{Solution}\)

  我切掉了，但没有完全切掉。

  画画图，在数轴上，画出向右行动的蓝色箭头和向左行动的红色箭头。注意到换卡本质上是交换始发站点，那么重合的红蓝箭头是能相互抵消的！如图：

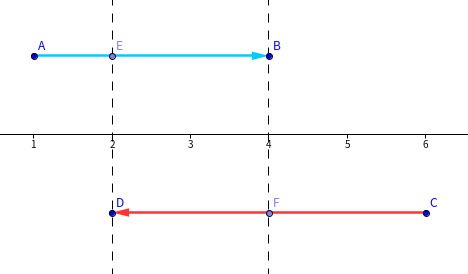
\(\vec{AB},\vec{CD}\) 互换起点，变为 \(\vec{AE},\vec{CF}\)，长度之和减少 \(2|DF|\)，并且 \(\vec{AE},\vec{FC}\) 仍旧能与其他向量进行互换操作。

  不难证明，对于数轴上 \([k,k+1]\)，覆盖它的红、蓝向量的数量的较小者就是这段区间被抵消的次数，且我们一定能构造方案取到这一下界，用向量总长减去它就求得最小花费。

  考虑方案的构造，注意到次数限制 \(4\times10^5=4\max\{n\}\)，猜测“抵消”操作能够在 \(n\) 次换卡操作内完成，那么每次换卡就得让一个向量无法再与其他向量抵消。理性分析，我们分别维护蓝色向量和红色向量的小根堆，按 \((\text{左侧点},\text{右侧点})\) 的偏序关系分别取出最小者，设为 \(\boldsymbol u,\boldsymbol v\)。若它们没有公共区间则必然有一个已经无用；否则，分类讨论：

• \(e(\boldsymbol u)\le s(\boldsymbol v)\)，即红色向量右端点靠右，如图：

  

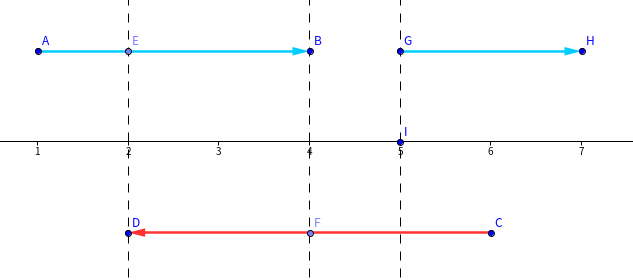
  \(\boldsymbol u=\vec{AB}\) 用完必然被丢掉，而 \(\vec{FD}\) 会被抵消，我们可以放心地让 \(A,C\) 在 \(B(F)\) 点会合换卡。但是！不能走回头路的限制带来一个问题：若存在 \(\vec{GH}\)，\(C\) 就无法与 \(G\) 换卡了！

  解决方法形象而自然：红色向量向左而扫描方向向右，那么红色向量上的会合点不得不会从左到右出现，那我们反过来以栈的顺序指挥红色向量不就好啦？

• \(e(\boldsymbol u)>s(\boldsymbol v)\)，即蓝色向量的右端靠右，与上个情况恰好相反，我们需要立即将操作方案加入答案再做后续计算。

  最后，复杂度 \(\mathcal O(n\log n)\) 就能构造好方案啦。

\(\mathcal{Code}\)

/* Clearink */

#include <queue>
#include <cstdio>
#include <vector>
#include <cassert>

#define rep( i, l, r ) for ( int i = l, rep##i = r; i <= rep##i; ++i )
#define per( i, r, l ) for ( int i = r, per##i = l; i >= per##i; --i )

inline int rint() {
    int x = 0, s = getchar();
    for ( ; s < '0' || '9' < s; s = getchar() );
    for ( ; '0' <= s && s <= '9'; s = getchar() ) x = x * 10 + ( s ^ '0' );
    return x;
}

template<typename Tp>
inline void wint( const Tp x ) {
    if ( 9 < x ) wint( x / 10 );
    putchar( x % 10 ^ '0' );
}

inline int imin( const int a, const int b ) { return a < b ? a : b; }
inline int imax( const int a, const int b ) { return a < b ? b : a; }

typedef long long LL;

const int MAXN = 1e5, MAXM = 1e6;
int n, m, s[MAXN + 5], e[MAXN + 5], fin[MAXN + 5];

struct Atom {
    int l, r, id;
    inline bool operator < ( const Atom& t ) const {
        return !( l != t.l ? l <= t.l : ( r != t.r ? r <= t.r : id <= t.id ) );
    }
};
std::priority_queue<Atom> seg[2];
std::vector<Atom> plan;

inline void action( const Atom& u, const Atom& v, const int p ) {
    if ( u.l != p ) plan.push_back( { u.id, p, 0 } );
    if ( v.r + 1 != p ) plan.push_back( { v.id, p, 0 } );
    plan.push_back( { u.id, v.id, 1 } );
}

inline void solve( LL& ans ) { // strange...
    if ( seg[0].empty() || seg[1].empty() ) return ;
    Atom u( seg[0].top() ), v( seg[1].top() );
    if ( u.r < v.l ) seg[0].pop(), solve( ans );
    else if ( v.r < u.l ) seg[1].pop(), solve( ans );
    else {
        seg[0].pop(), seg[1].pop();
        int il = imax( u.l, v.l ), ir = imin( u.r, v.r );
        ans -= ir - il + 1 << 1;

        if ( u.r <= v.r ) {
            if ( u.r < v.r ) seg[1].push( { u.r + 1, v.r, v.id } );
            solve( ans ), action( u, v, u.r + 1 );
        } else {
            if ( v.r < u.r ) seg[0].push( { v.r + 1, u.r, u.id } );
            action( u, v, v.r + 1 ), solve( ans );
        }
    }
}

int main() {
    freopen( "subway.in", "r", stdin );
    freopen( "subway.out", "w", stdout );

    for ( int T = rint(); T--; ) {
        n = rint(), m = rint();
        for ( ; !seg[0].empty(); seg[0].pop() );
        for ( ; !seg[1].empty(); seg[1].pop() );
        plan.clear();

        LL ans = 0;
        rep ( i, 1, n ) {
            fin[i] = s[i] = rint(), e[i] = rint();
            if ( s[i] < e[i] ) {
                ans += e[i] - s[i], seg[0].push( { s[i], e[i] - 1, i } );
            } else {
                ans += s[i] - e[i], seg[1].push( { e[i], s[i] - 1, i } );
            }
        }

        solve( ans );

        wint( ans ), putchar( ' ' );
        for ( const Atom& a: plan ) if ( !a.id ) fin[a.l] = a.r;
        rep ( i, 1, n ) if ( fin[i] != e[i] ) {
            plan.push_back( { i, e[i], 0 } );
        }
        assert( plan.size() <= 4e5 );
        wint( plan.size() ), putchar( '\n' );
        for ( const Atom& a: plan ) {
            wint( a.id ), putchar( ' ' );
            wint( a.l ), putchar( ' ' );
            wint( a.r ), putchar( '\n' );
        }
    }
    return 0;
}

\(\mathcal{Details}\)

  挺逗的，考场上想到了逆序操作却忽略了一部分操作需要正序，“对称”的坑点只注意到一个……补题发现把循环换成代码里的递归再调一调语句顺序就过了。长记性呐。