平衡二叉树（c++实现）续

！！版权声明：本文为博主原创文章，版权归原文作者和博客园共有，谢绝任何形式的 转载！！

作者：mohist

--- 欢迎指正---

题外话：上一篇关于平衡二叉树文章中，我都没说自己是怎么理解的。别人终归就是别人的。但别人真的是写的棒棒的。

这里续平衡二叉树的其他方法：

二叉树的 层次遍历   。

层次遍历，原则：从上到下，从左到右。

1、使用队列：

　　思路：

　　A、首先将根结点入队

　　B、再输出队首的值

　　C、若队首结点的左孩子不为空，将其入队

　　D、若队首结点的右孩子不为空，将其入队

　　E、因为已经输出队首的值，这时，需要将其出队。

　　F、反复执行A到E的步骤。直到树的最后一个元素。

　　分析：

　　执行过上面的步骤 E，此时，队列中对头的元素就是上次以入队的元素，若步骤C中队首的左孩子不为空，左孩子就是现在的队首。当执行下一次循环是，首先输出的就是左孩子了。同理，步骤D中的右孩子如果入队，下次循环执行输出的就是它了。以此类推。

2、上源码：

　　例子中使用的根结点结构：

struct node
{
    int data;
    int height;
    node *lc;
    node *rc;
    node()
        : data(0)
        , height(0)
        , lc(0)
        , rc(0)
    {

    }
};

使用队列，需要包含头文件

#include <queue>

队列实现：

 // 层次遍历树 （使用队列）
    void layer_order()
    {

        cout << endl << endl << "层次遍历,是用队列完成" << endl;
        queue<node*> vq;

        if (NULL != root)
            vq.push(root);

        // 队列不为空，继续遍历
        while (false == vq.empty())
        {
            cout << vq.front()->data << " -> ";

            // 若左孩子不为空，则继续加入队列
            if ( NULL != vq.front()->lc )
            {
                vq.push(vq.front()->lc);
            }

            // 若右孩子不为空，则继续入队
            if (NULL  != vq.front()->rc)
                vq.push(vq.front()->rc);

            // 已经遍历输出的元素，出队
            vq.pop();
        }

        cout << endl << endl;
    }

我的测试结果：

4、其他方法　　

若不实用队列，怎么实现？

　　数组。前提，数组能够存放整棵树的结点、数组大小不会 爆栈 。有缺陷。

　　数组的化，模拟上面的队列输出，增加两个索引，一个用来添加树的结点元素用，一个用来输出元素用。

上代码：

// 层次遍历，不是用队列，使用数组完成
    void layer_order_arr()
    {
        cout << endl << endl << " 层次遍历，不是用队列，使用数组完成 " << endl;

        // 定义指针数组的大小
        const int arr_len = 100;
        // 保存结点指针
        node *arr[arr_len] = {0};

        // 添加元素索引，添加到数组时使用
        int in_index = 0;

        // 输出元素索引，输出元素使用
        int out_index = 0;

        // 添加结点
        if (NULL != root)
            arr[in_index++] = root;

        // 若 添加元素索引大于输出元素索引，说明数组中还有没有输出的元素
        while ( in_index > out_index)
        {
            // 输出
            cout << arr[out_index]->data << " -> ";

            // 若左子树不为空，将其添加到数组
            if (NULL != arr[out_index]->lc)
                arr[in_index++] = arr[out_index]->lc;

            // 若右子树不为空，将其添加到数组
            if (NULL != arr[out_index]->rc)
                arr[in_index++] = arr[out_index]->rc;

            // 输出索引指向数组的下一个元素
            out_index++;
        }
    }

　　数组的方式输出结果：

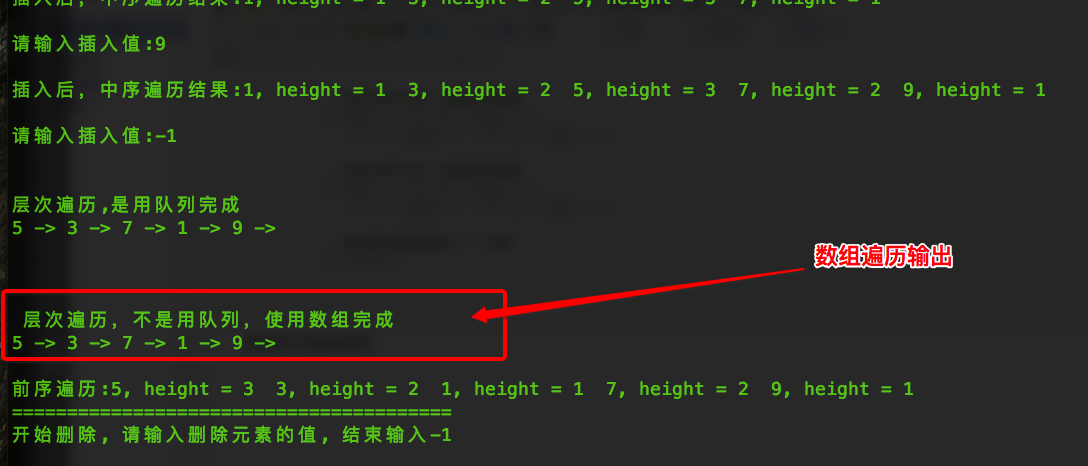
GitHub地址： https://github.com/mohistH/base_data_structure