python 回归分析

一、线性回归

1 绘制散点图

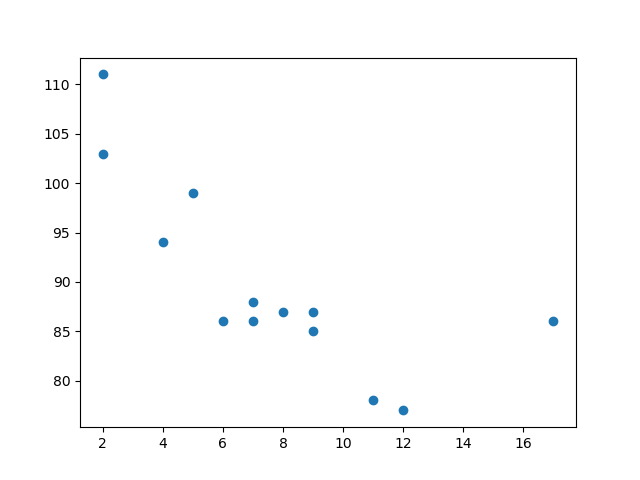
import matplotlib.pyplot as plt

x = [5,7,8,7,2,17,2,9,4,11,12,9,6]
y = [99,86,87,88,111,86,103,87,94,78,77,85,86]

plt.scatter(x, y)
plt.show()

结果：

2 导入 scipy 并绘制线性回归线：

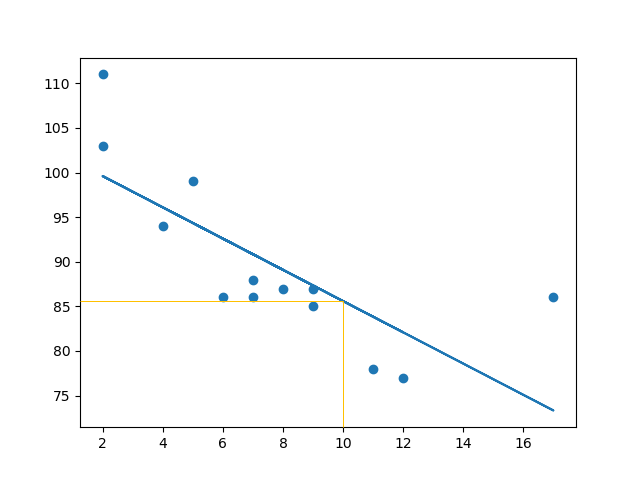
import matplotlib.pyplot as plt
from scipy import stats

x = [5,7,8,7,2,17,2,9,4,11,12,9,6]
y = [99,86,87,88,111,86,103,87,94,78,77,85,86]

slope, intercept, r, p, std_err = stats.linregress(x, y)

def myfunc(x):
  return slope * x + intercept

mymodel = list(map(myfunc, x))

plt.scatter(x, y)
plt.plot(x, mymodel)
plt.show()

结果：

二、多项式回归

　　如果数据点显然不适合线性回归（穿过数据点之间的直线），那么多项式回归可能是理想的选择。像线性回归一样，多项式回归使用变量 x 和 y 之间的关系来找到绘制数据点线的最佳方法。

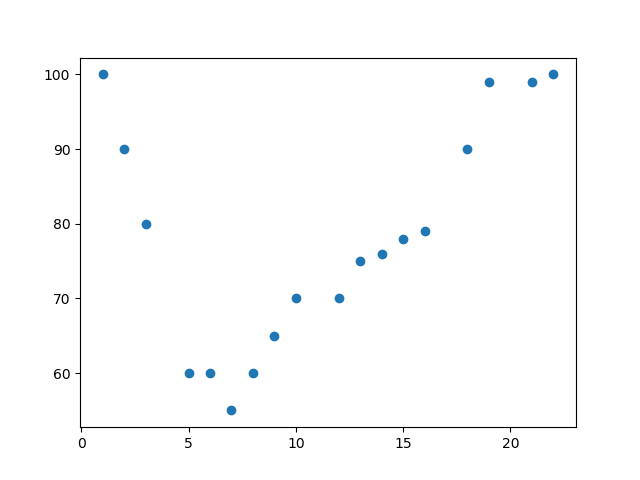
1 绘制散点图

import matplotlib.pyplot as plt

x = [1,2,3,5,6,7,8,9,10,12,13,14,15,16,18,19,21,22]
y = [100,90,80,60,60,55,60,65,70,70,75,76,78,79,90,99,99,100]

plt.scatter(x, y)
plt.show()

结果：

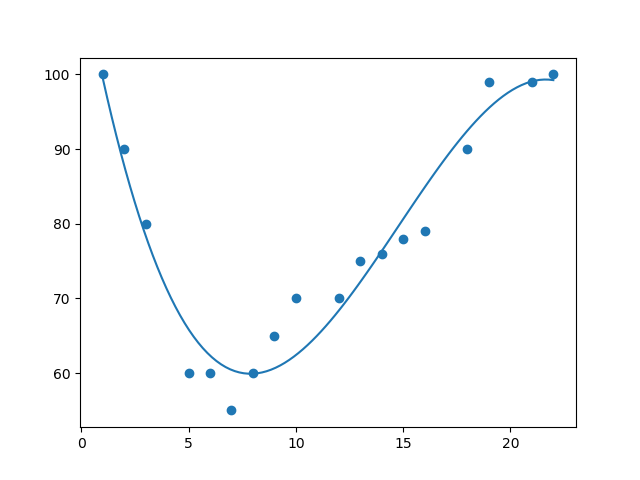
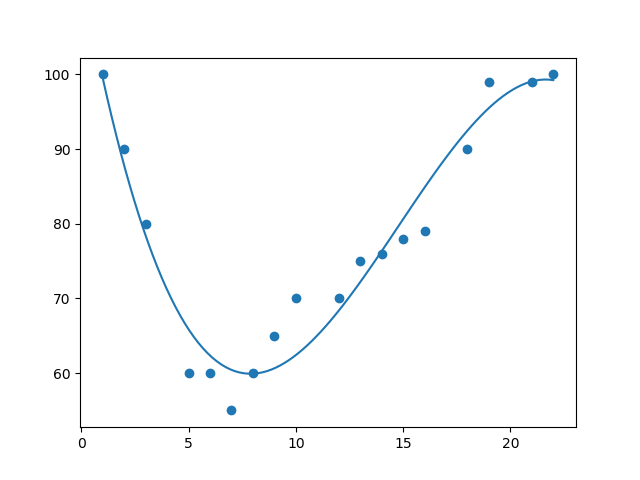
2 导入 numpy 和 matplotlib，然后画出多项式回归线：

import numpy
import matplotlib.pyplot as plt

x = [1,2,3,5,6,7,8,9,10,12,13,14,15,16,18,19,21,22]
y = [100,90,80,60,60,55,60,65,70,70,75,76,78,79,90,99,99,100]

mymodel = numpy.poly1d(numpy.polyfit(x, y, 3))

myline = numpy.linspace(1, 22, 100)

plt.scatter(x, y)
plt.plot(myline, mymodel(myline))
plt.show()

结果

R-Squared

重要的是要知道 x 轴和 y 轴的值之间的关系有多好，如果没有关系，则多项式回归不能用于预测任何东西。

该关系用一个称为 r 平方（ r-squared）的值来度量。

r 平方值的范围是 0 到 1，其中 0 表示不相关，而 1 表示 100％ 相关。

Python 和 Sklearn 模块将为您计算该值，您所要做的就是将 x 和 y 数组输入：

import numpy
from sklearn.metrics import r2_score

x = [1,2,3,5,6,7,8,9,10,12,13,14,15,16,18,19,21,22]
y = [100,90,80,60,60,55,60,65,70,70,75,76,78,79,90,99,99,100]

mymodel = numpy.poly1d(numpy.polyfit(x, y, 3))

print(r2_score(y, mymodel(x)))

三、多元回归

　　多元回归就像线性回归一样，但是具有多个独立值，这意味着我们试图基于两个或多个变量来预测一个值。

在 Python 中，我们拥有可以完成这项工作的模块。首先导入 Pandas 模块：

import pandas

Pandas 模块允许我们读取 csv 文件并返回一个 DataFrame 对象。

此文件仅用于测试目的，您可以在此处下载：cars.csv

df = pandas.read_csv("cars.csv")

然后列出独立值，并将这个变量命名为 X。

将相关值放入名为 y 的变量中。

X = df[['Weight', 'Volume']]
y = df['CO2']

提示：通常，将独立值列表命名为大写 X，将相关值列表命名为小写 y。

我们将使用 sklearn 模块中的一些方法，因此我们也必须导入该模块：

from sklearn import linear_model

在 sklearn 模块中，我们将使用 LinearRegression() 方法创建一个线性回归对象。

该对象有一个名为 fit() 的方法，该方法将独立值和从属值作为参数，并用描述这种关系的数据填充回归对象：

regr = linear_model.LinearRegression()
regr.fit(X, y)

现在，我们有了一个回归对象，可以根据汽车的重量和排量预测 CO2 值：

# 预测重量为 2300kg、排量为 1300ccm 的汽车的二氧化碳排放量：

predictedCO2 = regr.predict([[2300, 1300]])

完整实例：

import pandas
from sklearn import linear_model

df = pandas.read_csv("cars.csv")

X = df[['Weight', 'Volume']]
y = df['CO2']

regr = linear_model.LinearRegression()
regr.fit(X, y)

# 预测重量为 2300kg、排量为 1300ccm 的汽车的二氧化碳排放量：

predictedCO2 = regr.predict([[2300, 1300]])

print(predictedCO2)

打印回归对象系数值

import pandas
from sklearn import linear_model

df = pandas.read_csv("cars.csv")

X = df[['Weight', 'Volume']]
y = df['CO2']

regr = linear_model.LinearRegression()
regr.fit(X, y)

print(regr.coef_)