WHT, SLANT, Haar

目录

• 基本
  • 酉变换
• WALSH-HADAMARD TRANSFORMS
  • sequency-ordered WHT
• SLANT TRANSFORM
• Haar Transform

Gonzalez R. C. and Woods R. E. Digital Image Processing (Forth Edition)

基本

酉变换

一维的变换:

\[\mathbf{t} = \mathbf{A} \mathbf{f}, \\
\mathbf{f} = \mathbf{A}^{H} \mathbf{t}, \\
\mathbf{A}^H = {\mathbf{A}^*}^{T}, \mathbf{A}^H\mathbf{A} = \mathbf{I}.
\]

以及二维的变换:

\[\mathbf{T} = \mathbf{A} \mathbf{F} \mathbf{B}^T, \\
\mathbf{F} = \mathbf{A}^H \mathbf{T} \mathbf{B}^*, \\
\mathbf{A}^H\mathbf{A=I}, \mathbf{B}^{T}\mathbf{B}^* =\mathbf{I}.
\]

以一维的为例, 实际上就是

\[t_u = \sum_{x = 0}^{N-1} f_x s(x, u) = \mathbf{f}^T \mathbf{s}_u, u=0,1,\cdots, N-1,\\
\mathbf{s}_u = [s(0, u), s(1, u), \cdots, s(N-1, u)]^T.
\]

故

\[\mathbf{A} = [\mathbf{s}_0, \cdots, \mathbf{s}_{N-1}]^{T}.
\]

注: 下面假设:\(N=2^n\).

WALSH-HADAMARD TRANSFORMS

\[s(x, u) = \frac{1}{\sqrt{N}} (-1)^{\sum_{i=0}^{n-1}b_i(x)b_i(u)},
\]

注意, 这里\(b_i(u)\)表示\(u\)的二进制的第\(i\)位, 比如\(4\)的二进制为\(100\), 此时\(b_0 = 0, b_2=1\).

变换矩阵可以通过更通俗易懂的方式搭建:

\[\mathbf{A}_W = \frac{1}{\sqrt{N}} \mathbf{H}_N, \\
\mathbf{H}_{2N} =
\left [
\begin{array}{cc}
\mathbf{H}_N & \mathbf{H}_N \\
\mathbf{H}_N & -\mathbf{H}_N \\
\end{array}
\right ], \\
\mathbf{H}_{2} =
\left [
\begin{array}{cc}
1 & 1 \\
1 & -1 \\
\end{array}
\right ].
\]

sequency-ordered WHT

\[\mathbf{H}_{4} =
\left [
\begin{array}{cc}
1 & 1 & 1 & 1\\
1 & -1 & 1 & -1 \\
1 & 1 & -1 & -1\\
1 & -1 & -1 & 1 \\
\end{array}
\right ].
\]

可以发现, 第1行(\(u=0, 1, 2, 3\))的符号变换最快的(类似与DFT中的频率的概念), 故sequency-order, 即按照符号变换快慢的递增排列, 其公式如下:

\[s(x, u) = \frac{1}{\sqrt{N}}(-1)^{\sum_{i=0}^{n-1}b_i(x)p_i(u)}, \\
p_0 (u) = b_{n-1}(u), \\
p_{n-1-i}(u) = b_i(u) + b_{i+1}(u), \quad i = 0, \cdots, n-2.
\]

记\(\mathbf{H}_{W'}\)为sequency-order的, 则 \(\mathbf{H}_{W'}\)的第\(u\)行与\(\mathbf{H}_{W}\)的第\(v\)行存在如下的关系:

1. 考虑\(n\)bit的二进制, 则

\[u: (u_{n-1}u_{n-2}\cdots u_0),\\
v: (v_{n-1}v_{n-2}\cdots v_0).
\]

1. 将\(u\)转换成其gray code格式

\[g_i = u_i \oplus u_{i+1}, \quad i=0, \cdots, n-2\\
g_{n-1} = s_{n-1}.
\]

其中\(\oplus\)表示异或操作.

3. 对\(g\)进行bit-reverse, 即\(g_i, g_{n-1-i}\)调换位置, 则

\[v_i = g_{n-1-i}.
\]

举个例子, 假设\(n=3\), \(u=4 = (100)_2\), 则\(g = (110)_2\), \(v=(011)_2 = 3\). 即\(H_8'\)的第4行为\(H_8\)的第3行(注意均从0开始计数).

proof:

\[\begin{array}{ll}
p_{n-1-i}(u)
&= b_i(u) + b_{i+1}(u) \\
&\Leftrightarrow b_i(g) \\
&= b_{n-1-i}(v).
\end{array}
\]

注意\(\Leftrightarrow\), 是这样的, \(b_i + b_{i+1}\)仅有(0, 1, 2)三种可能性, 而\((-1)^1=-1\)否则为1，而\(b_i(g)=1\)恰好是\(b_i(u) + b_{i+1}(u) = 1\) (根据异或的定义可得), 故可能等价替换.

\[p_0(u) = b_0(v),
\]

是显然的, 证毕.

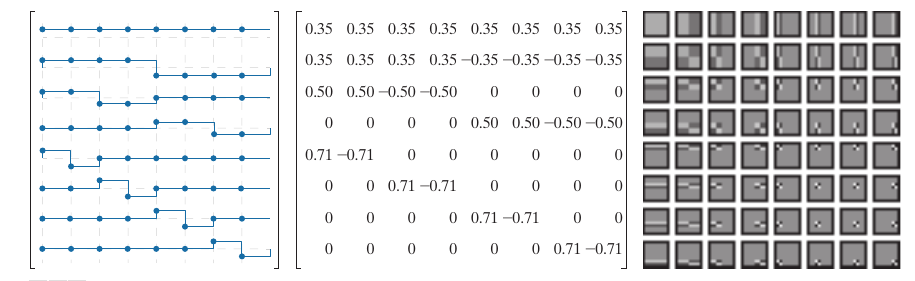
下图便是按照sequency增序的表示.

SLANT TRANSFORM

\[\mathbf{A}_{SI} = \frac{1}{\sqrt{N}}\mathbf{S}_N, \\
\mathbf{S}_{N} =
\left [
\begin{array}{cccccc}
1 & 0 & \mathbf{0} & 1 & 0 & \mathbf{0} \\
a_N & b_N & \mathbf{0} & -a_N & b_N & \mathbf{0} \\
0 & 0 & \mathbf{I}_{(N/2)-2} & 0 & 0 & \mathbf{I}_{(N/2)-2} \\
0 & 1 & \mathbf{0} & 0 & -1 & \mathbf{0} \\
-b_N & a_N & \mathbf{0} & b_N & a_N & \mathbf{0} \\
0 & 0 & \mathbf{I}_{(N/2)-2} & 0 & 0 & \mathbf-{I}_{(N/2)-2} \\
\end{array}
\right ]
\left [
\begin{array}{cc}
\mathbf{S}_{N/2} & \mathbf{0} \\
\mathbf{0} & \mathbf{S}_{N/2} \\
\end{array}
\right ], \\
\mathbf{S}_2 =
\left [
\begin{array}{cc}
1 & 1 \\
1 & -1 \\
\end{array}
\right ], \\
a_N = [\frac{3N^2}{4(N^2-1)}]^{1/2}, \\
b_N = [\frac{N^2-4}{4(N^2-1)}]^{1/2}.
\]

标准正交性质是容易证明的, 需要特别注意的是, 改变换矩阵是非对称的, 所以逆变换是需要计算逆的\(A_{SI}^{-1}\).

Haar Transform

Haar 是一种小波变换, 这里简单写一下.

\[s(x, u) = \frac{1}{\sqrt{N}} h_u(x / N), \quad x= 0,1,\cdots, N-1, \\
u = 2^p + q, \\
h_u(x) =
\left \{
\begin{array}{ll}
1 & u=0 \: \text{and} \: 0 \le x < 1, \\
2^{p/2} & u > 0 \text{and} \: q/2^p < (q + 0.5)/2^p, \\
-2^{p/2} & u > 0 \text{and} \: (q+0.5)/2^p < (q + 1)/2^p, \\
0 & \text{otherwise}.
\end{array}
\right .
\]