【机器学习基础】对 softmax 和 cross-entropy 求导

符号定义
对 softmax 求导
对 cross-entropy 求导
对 softmax 和 cross-entropy 一起求导
References

在论文中看到对 softmax 和 cross-entropy 的求导，一脸懵逼，故来整理整理。

以 softmax regression 为例来展示求导过程，softmax regression 可以看成一个不含隐含层的多分类神经网络，如 Fig. 1 所示。

Fig. 1 Softmax Regression.

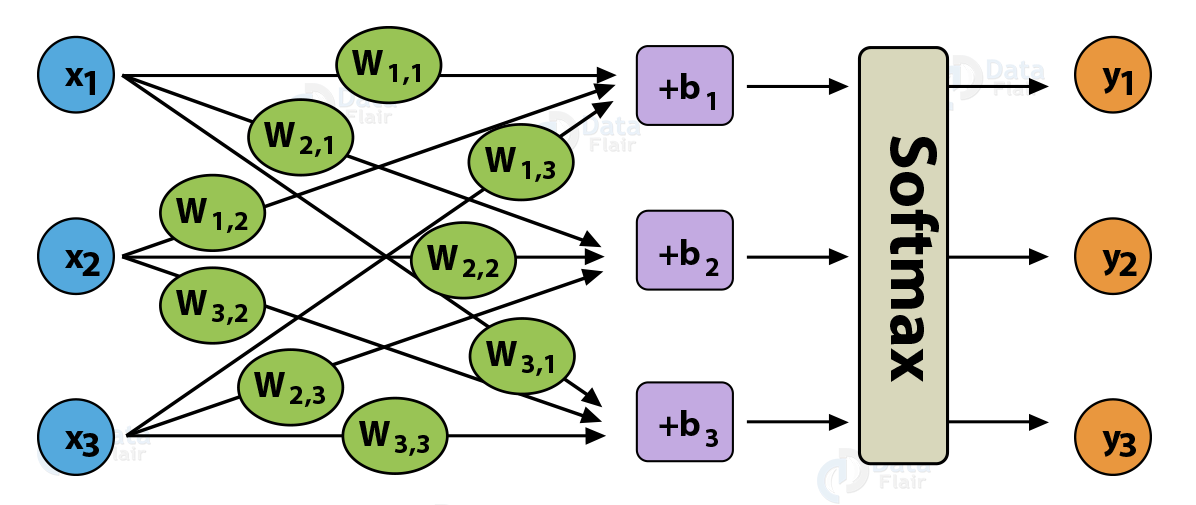
softmax regression 的矩阵形式如 Fig. 2 所示：

Fig. 2 Matrix Form.

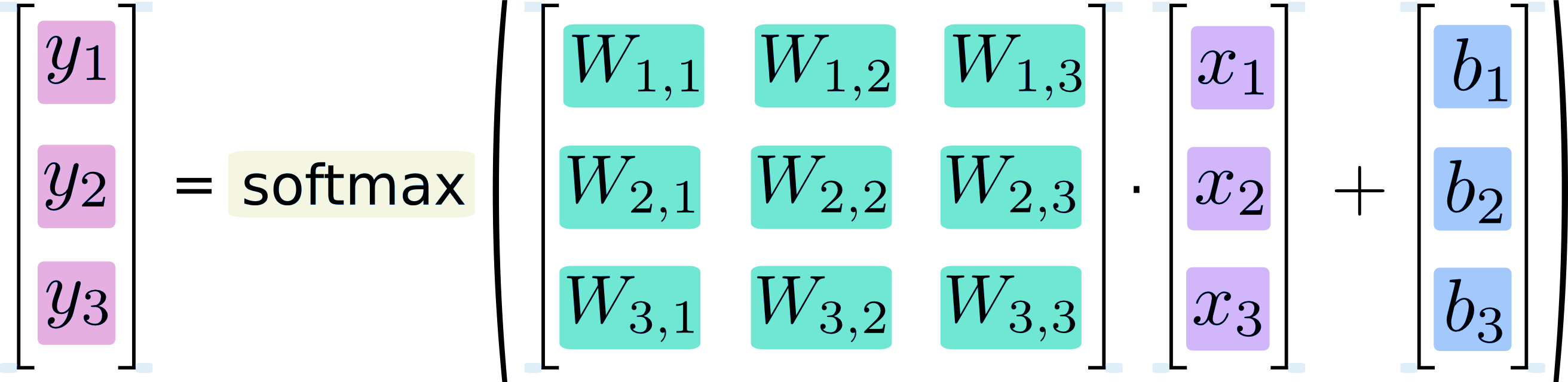
符号定义

如 Fig. 1 所示，$\bm x = [x_1, x_2, x_3]^{\top}$ 表示 softmax regression 的输入，$\bm y = [y_1, y_2, y_3]^{\top}$ 表示 softmax regression 的输出，$\bm W$ 为权重，$\bm b = [b_1, b_2, b_3]^{\top}$ 为偏置。

令 Fig. 2 中 softmax function 的输入为 $z_i = W_{i, 1}x_1 + W_{i, 2}x_2 + W_{i, 3}x_3 + b_i = W_{i}\bm x + b_i$，其中 $i= 1, 2, 3$，$W_{i}$ 表示权重矩阵 $\bm W$ 的第 $i$ 行；softmax function 的输出就是整个网络的输出，即 $\bm y$。

Note: Fig. 1 和 Fig.2 中权重 $W_{i, j}$ 表示第 $i$ 个输出和第 $j$ 个输入之间的联系，和一般的记法（即 $W_{i, j}$ 表示第 $i$ 个输入和第 $j$ 个输出之间权重）相差一个转置。

用 $m$ 表示输出的类别数，本文中 $m = 3$。

Note: softmax regression 指的是整个网络，softmax function 仅仅指的是激活函数。本文默认 softmax 代指激活函数，当表示整个网络时会明确说明 softmax regression。

对 softmax 求导

softmax 函数的表达式为：
\[
y_i = \frac{e^{z_i}}{\sum_{t = 1}^m e^{z_t}}
\tag{1}
\]

其中 $i= 1, 2, 3$。由式（1）可知，$y_i$ 与 softmax function 所有的输入 $z_j, j = 1,2,3.$ 都有关。
softmax function 的输出对其输入求偏导：
\[
\frac{\partial y_i}{\partial z_j}
= \frac{\partial \frac{e^{z_i}}{\sum_{t = 1}^m e^{z_t}}}{\partial z_j}
\tag{2}
\]

需要对式（2）中 $i = j$ 和 $i \not = j$ 的情况进行分别讨论。因为式（1）分子中仅含第 $i$ 项，式（2）中如果 $i = j$，那么导数 $\frac{\partial e^{z_i}}{\partial z_j} = e^{z_i}$，不为 0；如果 $i \not = j$，那导数 $\frac{\partial e^{z_i}}{\partial z_j} = 0$。

$i = j$，则式（2）为：
\[
\begin{split}
\frac{\partial y_i}{\partial z_j}
&= \frac{\partial \frac{e^{z_i}}{\sum_{t = 1}^m e^{z_t}}}{\partial z_j}
\\ &= \frac{e^{z_i} \cdot \sum_{t = 1}^m e^{z_t} - e^{z_i} \cdot e^{z_j} }{(\sum_{t = 1}^m e^{z_t})^2}
\\ &= \frac{e^{z_i}}{\sum_{t = 1}^m e^{z_t}} - \frac{e^{z_i}}{\sum_{t = 1}^m e^{z_t}} \cdot \frac{e^{z_j}}{\sum_{t = 1}^m e^{z_t}}
\\ &=y_i(1 - y_j)
\end{split}
\tag{3}
\]

当然，式（3）也可以写成 $y_i(1 - y_i)$ 或者 $y_j(1 - y_j)$，因为这里 $i = j$。

$i \not = j$，则式（2）为：
\[
\begin{split}
\frac{\partial y_i}{\partial z_j}
&= \frac{\partial \frac{e^{z_i}}{\sum_{t = 1}^m e^{z_t}}}{\partial z_j}
\\ &= \frac{0\cdot \sum_{t = 1}^m e^{z_t} - e^{z_i} \cdot e^{z_j} }{(\sum_{t = 1}^m e^{z_t})^2}
\\ &= - \frac{e^{z_i}}{\sum_{t = 1}^m e^{z_t}} \cdot \frac{e^{z_j}}{\sum_{t = 1}^m e^{z_t}}
\\ &= -y_iy_j
\end{split}
\tag{4}
\]

对 cross-entropy 求导

令 $\bm {\hat y} = [\hat{y}_1, \hat{y}_2, \hat{y}_3]^{\top}$ 为输入 $\bm x$ 真实类别的 one-hot encoding。

cross entropy 的定义如下：
\[
H(\bm {\hat y}, \bm y)
= - \bm {\hat y}^{\top} \log \bm y
= - \sum_{t = 1}^m \hat{y}_t\log y_t
\tag{5}
\]

对 cross entropy 求偏导：（$\log$ 底数为 $e$）
\[
\frac{\partial H(\bm {\hat y}, \bm y) }{\partial y_i}
= \frac{\partial [- \sum_{t = 1}^m \hat{y}_t\log y_t ]}{\partial y_i}
= - \frac{\hat{y}_i}{y_i}
\tag{6}
\]

$\bm {\hat y}$ 是确定的值，可以理解为样本的真实 one-hot 标签，不受模型预测标签 $\bm y$ 的影响。

对 softmax 和 cross-entropy 一起求导

\[
\begin{split}
\frac{\partial H(\bm {\hat y}, \bm y) }{\partial z_j}
&= \sum_{i = 1}^{m} \frac{\partial H(\bm {\hat y}, \bm y) }{\partial y_i} \frac{\partial y_i }{\partial z_j}
\\ &= \sum_{i = 1}^{m} -\frac{\hat{y}_i}{y_i} \cdot \frac{\partial y_i }{\partial z_j}
\\ &= \left(-\frac{\hat{y}_i}{y_i} \cdot \frac{\partial y_i }{\partial z_j}\right )_{i = j} + \sum_{i = 1 , i \not = j}^{m} -\frac{\hat{y}_i}{y_i} \cdot \frac{\partial y_i }{\partial z_j}
\\ &= -\frac{\hat{y}_j}{y_i} \cdot y_i(1-y_j) + \sum_{i = 1 , i \not = j}^{m} -\frac{\hat{y}_i}{y_i} \cdot -y_iy_j
\\ &= - \hat{y}_j + \hat{y}_jy_j + \sum_{i = 1 , i \not = j}^{m} \hat{y}_iy_j
\\ & = - \hat{y}_j + y_j\sum_{i = 1}^{m} \hat{y}_i
\\ &= y_j - \hat{y}_j
\end{split}
\tag{7}
\]

交叉熵 loss function 对 softmax function 输入 $z_j$ 的求导结果相当简单，在 tensorflow 中，softmax 和 cross entropy 也合并成了一个函数，tf.nn.softmax_cross_entropy_with_logits，从导数求解方面看，也是有道理的。

在实际使用时，推荐使用 tensorflow 中实现的 API 去实现 softmax 和 cross entropy，而不是自己写，原因如下：

都已经有 API 了，干嘛还得自己写，懒就是最好的理由；
softmax 因为计算了 exp(x)，很容易就溢出了，比如 np.exp(800) = inf，需要做一些缩放，而 tensorflow 会帮我们处理这种数值不稳定的问题。

References

TensorFlow MNIST Dataset and Softmax Regression - Data Flair
链式法则 - 维基百科
 Softmax函数与交叉熵 - 知乎