[DeeplearningAI笔记]神经网络与深度学习3.2_3.11(激活函数)浅层神经网络

觉得有用的话,欢迎一起讨论相互学习~Follow Me

3.2 神经网络表示

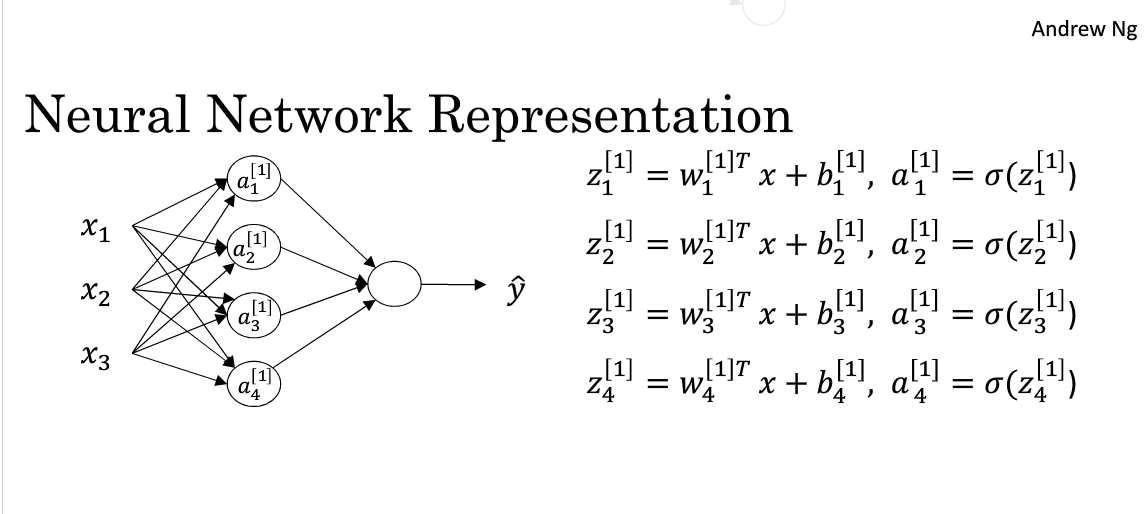
对于一个由输入层,隐藏层,输出层三层所组成的神经网络来说,输入层,即输入数据被称为第0层,中间层被称为第1层,输出层被称为第2层.所以这个神经网络被称为两层神经网络,我们不把输入层当做一个标准的层.

3.3 计算神经网络的输出

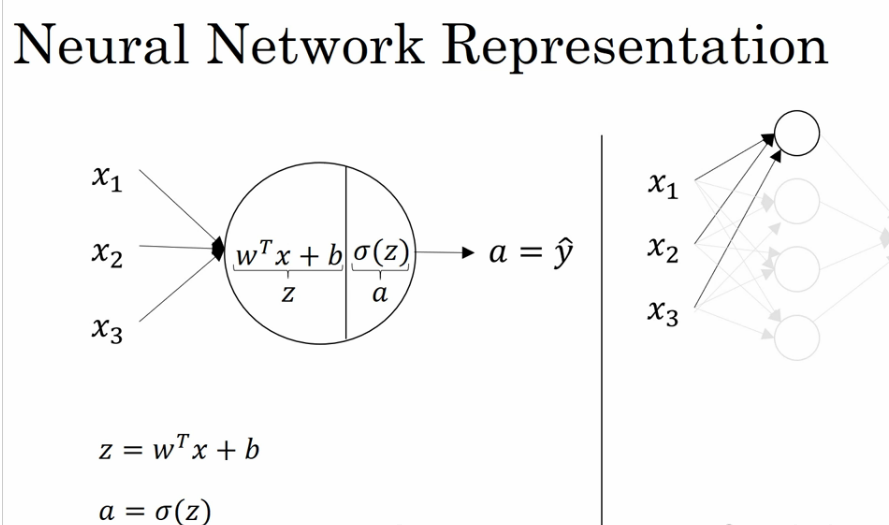
对于输入层的输入,我们把输入看做是一个矩阵,对于第一层的第一个神经元结点,计算\(W^T*x+b\)

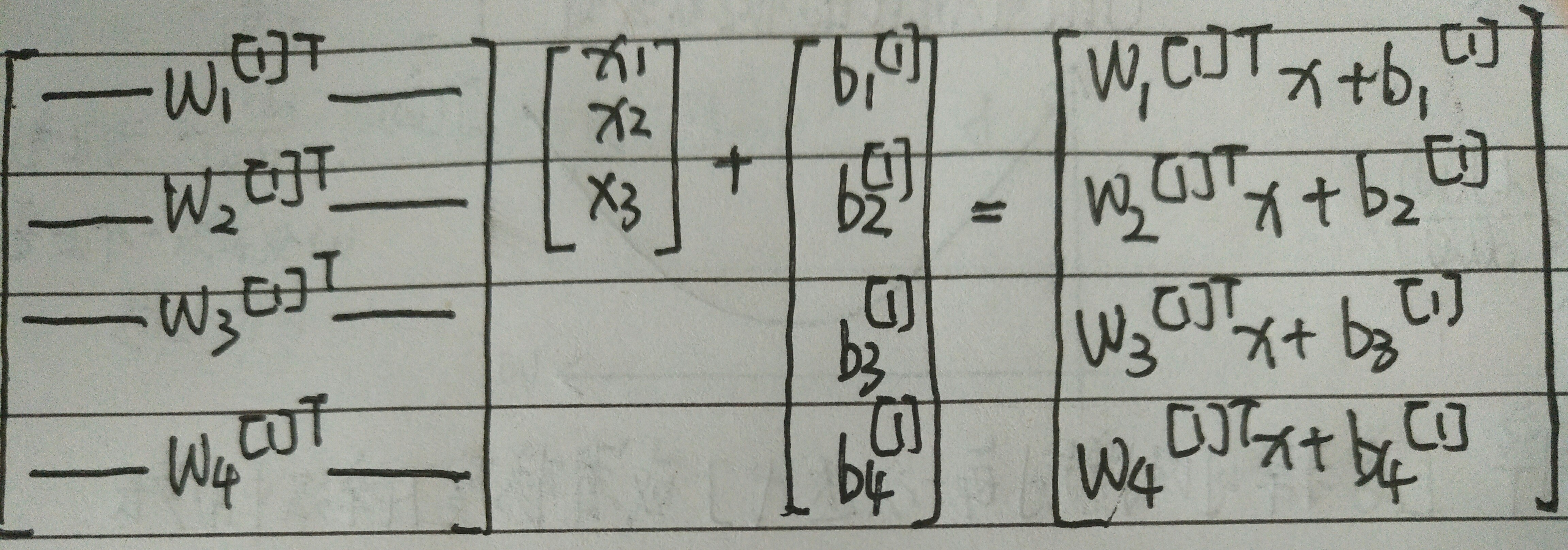
3.4 多个样本例子中的向量化

上一节讨论的是对于单个样本我们使用神经网络表示的方法,现在我们谈论的是对于多个输入样本的神经网络表示方法,类似的对于m个样本,我们只需要对其进行遍历即可.

在图中[]括号表示神经元层数,()表示样本数.

对于这些矩阵来说横向指标就对应了不同的训练样本,从左向右扫的时候,就扫过了整个训练集,在竖向中,竖向指标就对应了单一神经网络层里不同的节点.

3.6 激活函数

tanh function

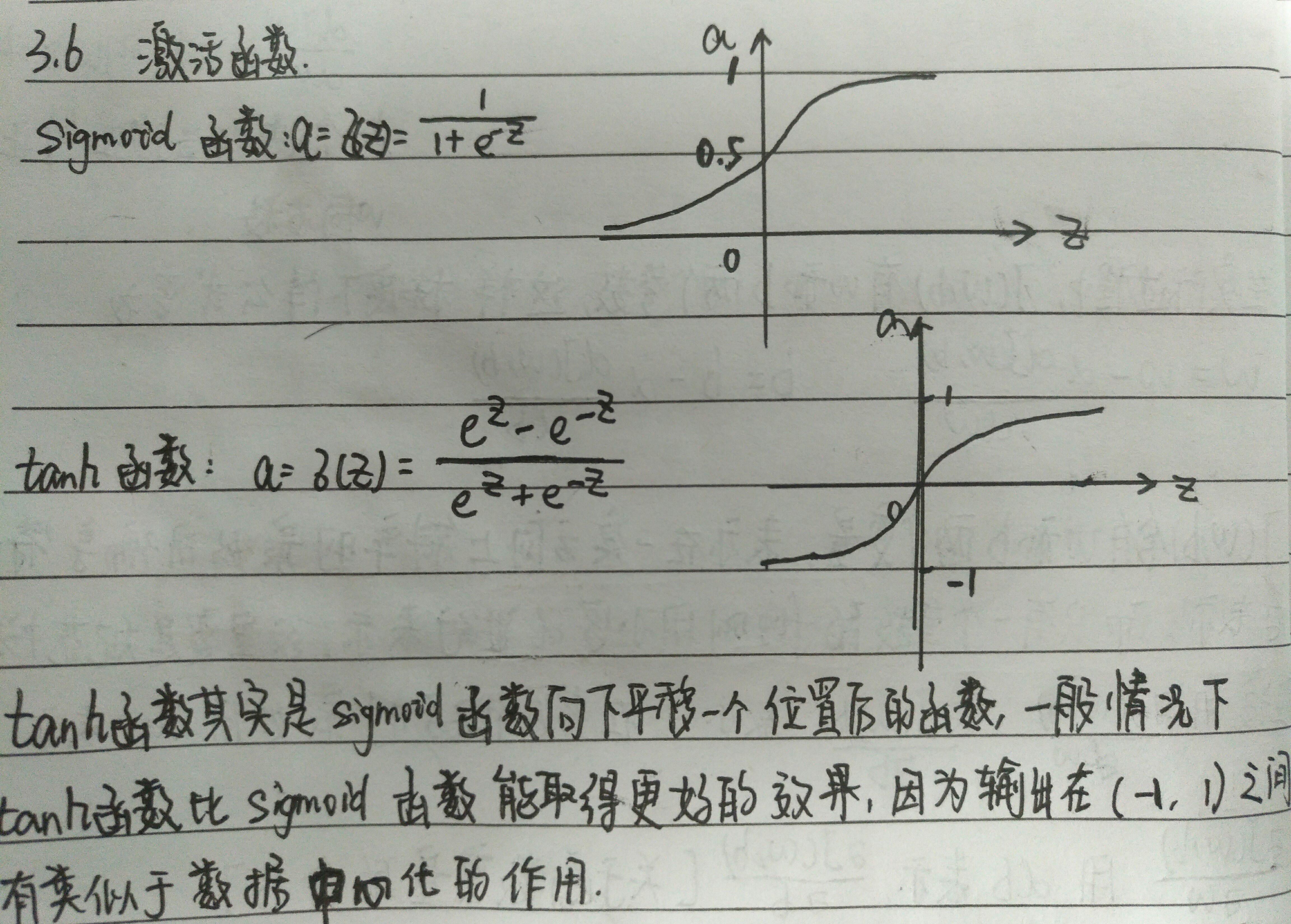
Angnew NG几乎不会使用sigmoid 函数,因为tanh函数几乎在任何方面多更加强大,但是对于输出层例外,因为在二元分类中,你可以使用sigmoid函数作为输出层的激活函数.但是对于sigmoid函数和tanh函数都有的缺点是,当z非常大或者非常小的时候,这个函数的梯度/斜率会变得很小.

ReLU function

ReLU(修正线性单元)

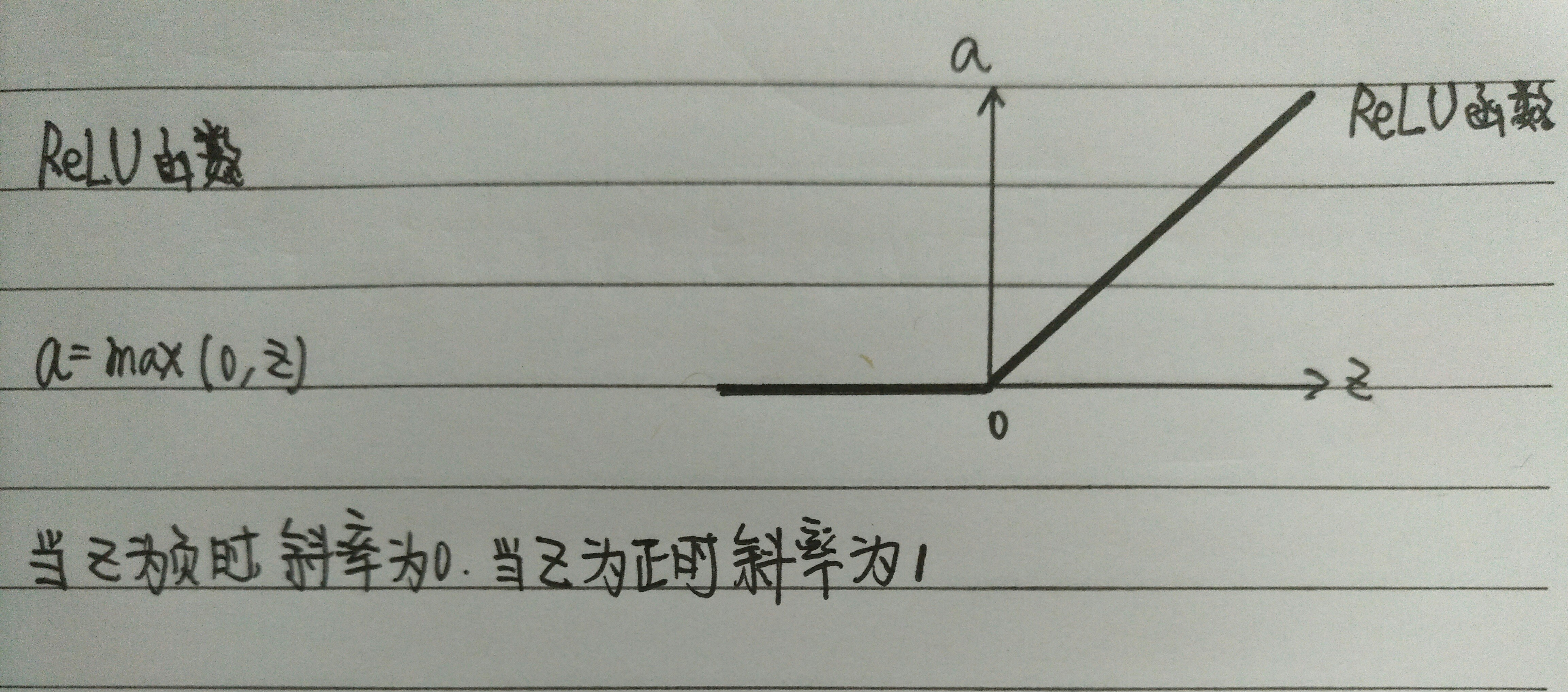
经验法则

如果你在做二元分类,那么sigmoid函数很适合作为输出层的激活函数,然后其他所有单元都用ReLU(现在已经几乎成为了几乎函数的默认选择),如果你不确定隐藏层的激活函数是什么可以大胆的尝试使用ReLU函数.对于ReLU函数在负数时斜率为0的问题,也给出了解决方案,被称为带泄露的ReLU(leaky ReLU).当z为负数时,函数不再为0,它有一个很平缓的斜率.leaky ReLU函数通常比ReLU函数更好.但是并没有ReLU函数这么常用.如果一定要选择一个激活函数,Angnew NG通常使用ReLU函数.使用ReLU函数的优势在于其在正数范围的斜率恒定为1,没有斜率接近0时减缓学习速率的情况.虽然对于ReLU函数来说其值在负数区间内的值是0,但是在实际实践中,有足够多的隐藏单元令z大于0.所以对大多数的训练样本来说还是相当快的.

总结

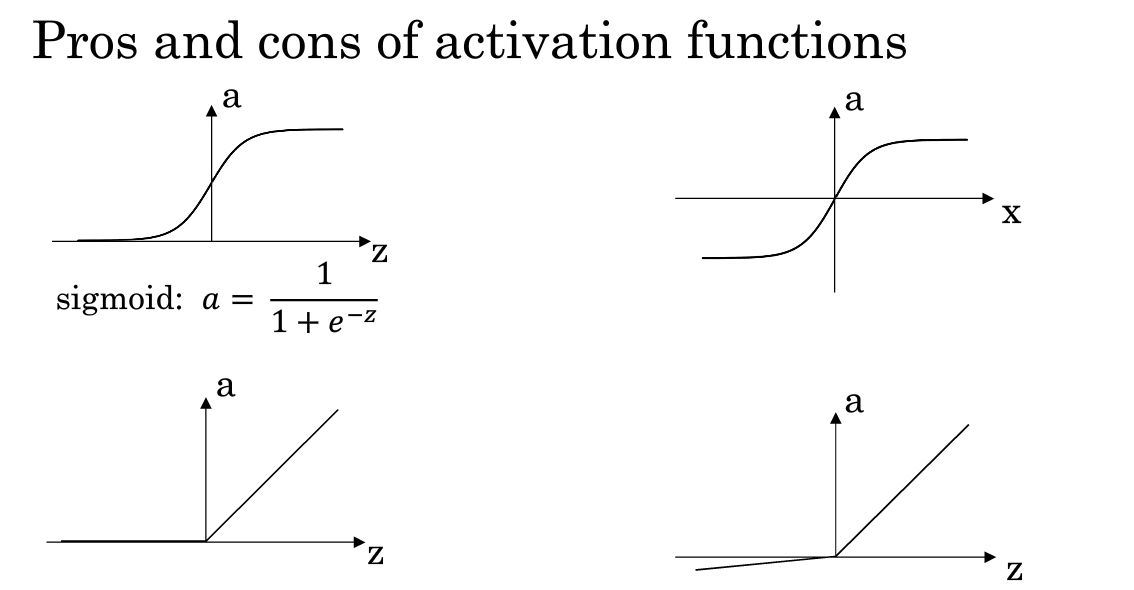
3.7 为什么需要非线性激活函数

我们为什么一定要把神经网络计算得到的结果经过激活函数输出呢?而不是直接使\(a^{[i]}=z^{[i]}\).其实使\(a^{[i]}=z^{[i]}\)有很官方的名字,称为恒等激活函数/线性激活函数.这样如果使用恒等激活函数,则会发现这是一种输入值的线性组合.在深度网络中,会发现,这不过是输入的简单的线性组合,还不如去掉所有的隐藏层,线性隐藏层一点用也没有.如果你要计算的是回归问题,也许可以在输出层使用线性激活函数.除此以外,几乎没有地方会用到线性激活函数.

3. 8 激活函数的导数

sigmoid function

对于sigmoid函数设\(g(z)=\frac{1}{1+e^{-z}}\),那么对于g(z)函数来说\(g^{'}(z)=g(z)(1-g(z))\)这正好解释了,当z非常大的时候g(z)趋向于1,则此时 \(g^{'}(z)\) 趋向于0,也就是说这时候函数会停止增长,类似于一条直线的形式.而在z=0时,\(g^{'}(z)\)会趋向于1/4.

tanh function

对于tanh函数设\(g(z)=\frac{e^{z}-e^{-z}}{e^{z}+e^{-z}}\),那么对于函数\(g^{'}(z)=1-(tanh(z))^{2}\)

ReLU function

对于ReLU函数设\(g(z)=max(0, z)\),

\(g^{'}(z)=\)$\begin{cases}

0 & z<0 \

1 & z>0 \

undefine & z=0 \

\end{cases}

$

leaky ReLU

对于Leaky ReLU函数设\(g(z)=max(0.01z, z)\),

\(g^{'}(z)=\)$\begin{cases}

0.01 & z<0 \

1 & z>0 \

undefine & z=0 \

\end{cases}

$

3.11 随机初始化

随机初始化十分重要,对于logistic regression 我们可以将权重设置为0,但是如果将所有层权重设置为0,在使用梯度下降法,那会完全无效.因为通过归纳法证明同一层的不同神经元如果都初始化为0,那么经过相同的激活函数,在计算反向传播算法时,其下降梯度即\(dz^{[i]}_{m}=dz^{[i]}_{n}\).即同一层不同神经元对于权重的下降梯度完全相同,这样一个隐藏层有多个神经元和隐藏层拥有一个神经元效果相同.解决这个的方法就是随机初始化参数.

我们一般将w和b设置为很小的随机值,因为在方程z=w*x+b中,如果计算得到的z值过大,会落在sigmoid或者是tanh函数的平缓地带,这样使用梯度下降法时会非常慢.也会学习的非常慢.